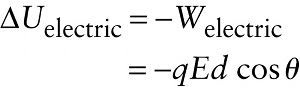Electric potential energy for a charge in a uniform electric field (17-2)
Question
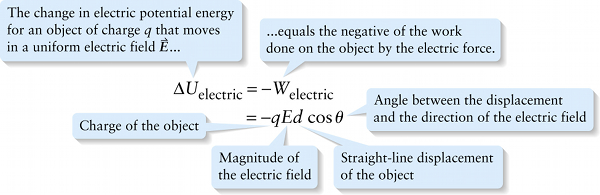
The change in electric potential energy for an object of charge \(q\) that moves in a uniform electric field \(\vec{E}\)...
{"title":"The change in electric potential energy for an object of charge q that moves in a uniform electric field vector E..","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"21,3,47,32\"}]"} {"title":"…equals the negative of the work done on the object by the electric force.","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"173,1,206,32\"}]"} {"title":"Angle between the displacement and the direction of the electric field","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"283,54,301,80\"}]"} {"title":"Straight-line displacement of the object","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"210,54,233,81\"}]"} {"title":"Magnitude of the electric field","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"189,54,212,82\"}]"} {"title":"Charge of the object","description":"Incorrect","type":"incorrect","color":"#800000","code":"[{\"shape\":\"rect\",\"coords\":\"171,62,190,85\"}]"}Review
This analogy between gravitational force and electric force tells us how to write the change in electric potential energy for an object of charge \(q\) that undergoes a displacement \(\vec{d}\) in the presence of a uniform electric field \(\vec{E}\) (Figure 17-3a). Following the same steps that we used to find Equation 17-1 above, you can see that if \(\theta\) is the angle between the directions of \(\vec{d}\) and \(\vec{E}\), then the work done on the charge by the electric force \(\vec{F} = q\vec{E}\) is \(W_{\mathrm{electric}} = qEd \cos{\theta}\). The change in electric potential energy equals the negative of the electric work done on the charge: