Electric potential related to electric potential energy (17-5)

Review

Our discussion in Section 17-2 shows that if a point charge $q$ changes position, the potential energy change $U_{\mathrm{electric}}$ depends on both the magnitude and the sign (positive or negative) of $q$ (see Figure 17-3). We can simplify things by considering the potential energy per charge—that is, the electric potential energy for a charge at a given position divided by the value of that charge. We call this quantity the electric potential and denote it by the symbol $V$:

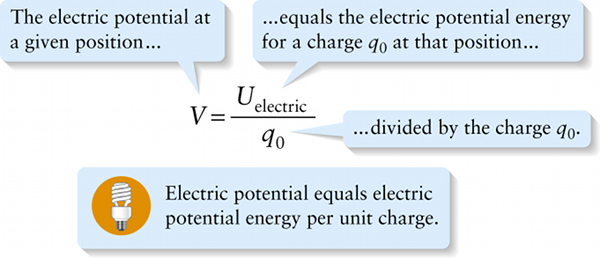
We call the charge $q_0$ the test charge: Its charge has such a small magnitude that it doesn’t affect the other charges that create the electric field in which $q_0$ moves. Because we divide out the value of $q_0$, the value of the potential $V$ at a given position does not depend on the value of the point charge $q_0$ that we place there. Instead, $V$ is determined by the other charges that produce the electric field at the position where we place the test charge.