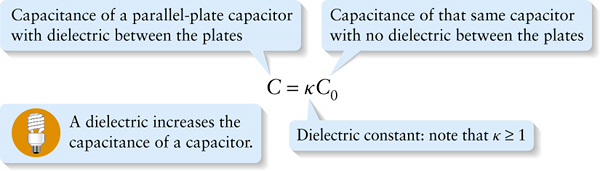
Chapter 17. Capacitance of a parallel-plate capacitor with a dielectric (17-28)

Question

tepGWqbaQZIM7h65GU35PdoIHsaSLw9BkZtEXBPRCz0ZGVruajrTzQo8MqhLrkwA7lO1iF5H43OoomUkTLha7zJpiuxO65SLx/ieBmw+rcE=

{"title":"Capacitance of a parallel-plate capacitor with dielectric between the plates","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,6,40,59\"}]"} {"title":"Capacitance of that same capacitor with no dielectric between the plates","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"139,7,176,54\"}]"} {"title":"Dielectric constant: note that k ≥ 1","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,7,137,54\"}]"}

Question

V1dNZJVK/AInSt1l30gk+HLIt9Z2CPaOTYO3hAM6UfeIZetIlPg1UX6Hf8bdQtENZAHVQmFQkuCxOiybImWg6BOKOVnIh8ZkmybISA==

{"title":"Capacitance of a parallel-plate capacitor with dielectric between the plates","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,6,40,59\"}]"} {"title":"Capacitance of that same capacitor with no dielectric between the plates","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"139,7,176,54\"}]"} {"title":"Dielectric constant: note that k ≥ 1","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,7,137,54\"}]"}

Question

gRqRGbFbto99+EAE7jvgOFkhSymXgnxrbTV0rVk6jD4Zi05NM/FbZ4p3zYVlR45ZcL6Btw==

{"title":"Capacitance of a parallel-plate capacitor with dielectric between the plates","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,6,40,59\"}]"} {"title":"Capacitance of that same capacitor with no dielectric between the plates","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"139,7,176,54\"}]"} {"title":"Dielectric constant: note that k ≥ 1","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,7,137,54\"}]"}

Review

As an example, Table 17-1 tells us that the dielectric constant of porcelain is \(\kappa = 5.8\). From Equation 17-28, the capacitance of a capacitor with porcelain filling the space between its plates is 5.8 times greater than an identical capacitor with vacuum between its plates. That’s fundamentally because the electric field in the porcelain-filled capacitor is only \(1/5.8 = 0.17\) as greater than an identical capacitor with vacuum between its plates. That's fundamentally because the electric field in the porcelain-filled capacitor is only \(1/5.8 = 0.17\) as great as for an identical vacuum capacitor carrying the same charge (Equation 17-27).