Chapter 21. Power for a resistor (18-24)
Question
3QxhZQDQ+v7PQP5i1CxHMkd1Nah3d96AnwDEVA==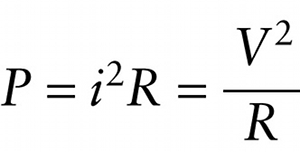
Question
MUUs2yh1zJAdGmNKxDUBqvbbc8u9otbaqEfLcMiEu/k=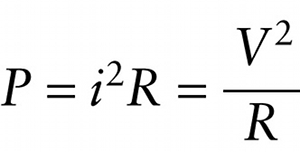
Question
mMeCJb9LYec2D9sQzVDfFznir2p5Al8/VvdKHLmgcLA=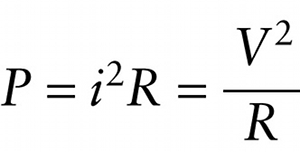
Question
Be2tWOBxdYEcD2Q3lcFQtZd/9iWt2NqbSFGqNvkPlwY=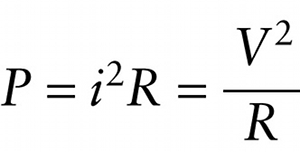
Review
Figure 21-2 graphs the voltage \(V(t)\) as a function of time. The angular frequency \(\omega\) of the voltage (in rad/s) is related to the frequency \(f\) of the voltage (in Hz) by the same relationship we used in Section 12-3 for simple harmonic motion:
\(\omega = 2\pi{f}\)
The period \(T\) of the oscillation is equal to \(1/f\). For example, in the United States and Canada ac voltage is applied at a frequency \(f = 60\ \mathrm{Hz}\), so the period of oscillation is \(T = 1/f = 1/ (60\ \mathrm{Hz})= 0.017 \mathrm{s}\) and the angular frequency is \(\omega = 2\pi{f} = (2\pi\mathrm{rad})\ (60\ \mathrm{Hz}) = 3.8 \times 10^2\ \mathrm{rad}/s\).
If we attach a source of ac voltage described by Equation 21-1 to a resistor of resistance \(R\), we can still use Equation 18-24 to calculate the power that flows into the resistor:
.
