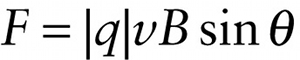Magnitude of magnetic force on a moving charged particle (19-1)

Question 1 of 5

Question

Magnitude of the magnetic force on a moving charged particle

{"title":"Magnitude of the magnetic force on a moving charged particle","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,4,34,49\"}]"} {"title":"Magnitude of the magnetic field","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"159,8,190,48\"}]"} {"title":"Angle between the direction of the particle’s velocity \\vector v and the direction of the magnetic field vector B","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"268,6,297,48\"}]"} {"title":"Speed of the particle","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"132,16,158,49\"}]"} {"title":"Magnitude of the particle’s charge","description":"Incorrect","type":"incorrect","color":"#800000","code":"[{\"shape\":\"rect\",\"coords\":\"95,17,122,57\"}]"}

Question

Angle between the direction of the particle’s velocity $\vec{v}$ and the direction of the magnetic field $\vec{B}$

{"title":"Magnitude of the magnetic force on a moving charged particle","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,4,34,49\"}]"} {"title":"Magnitude of the magnetic field","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"159,8,190,48\"}]"} {"title":"Angle between the direction of the particle’s velocity \\vector v and the direction of the magnetic field vector B","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"268,6,297,48\"}]"} {"title":"Speed of the particle","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"132,16,158,49\"}]"} {"title":"Magnitude of the particle’s charge","description":"Incorrect","type":"incorrect","color":"#800000","code":"[{\"shape\":\"rect\",\"coords\":\"95,17,122,57\"}]"}

Review

The SI units of magnetic field are tesla (T). In Equation 19-1, if charge $q$ is in coulombs (C), speed $v$ is in meters per second (m/s), and magnetic field magnitude $B$ is in tesla (T), the force $F$ is in newtons (N). So $1\ \mathrm{T}$ is the same as $1\ \mathrm{N}\ \cdot \mathrm{s} / (\mathrm{C} \cdot \mathrm{m}$ ) or $1\ \mathrm{N} /(\mathrm{A} \cdot \mathrm{m}$ ). (Recall that one ampere equals one coulomb per second: $1\ \mathrm{A} = 1\ \mathrm{C}/\mathrm{s}$ .)