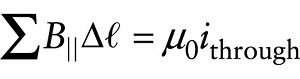Ampère’s law (19-13)

Question 1 of 3

Question

Current through the Amperian loop

{"title":"Circulation of magnetic field around an Amperian loop","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"43,18,66,51\"}]"} {"title":"Permeability of free space","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"162,27,188,56\"}]"} {"title":"Current through the Amperian loop","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"200,22,212,52\"}]"}

Review

Equation 22-7 tells us that a circulating electric field is produced by a magnetic field that changes over time. In Section 19-7 we learned that a circulating magnetic field is produced by electric charges in motion, that is, by a current. The mathematical expression of this statement is Ampère’s law:

Figure 22-8a shows an application of Ampère’s law that we introduced in Section 19-7: the magnetic field due to a long, straight, current-carrying wire. The current through each loop in the figure is equal to the current in the wire, so for each loop $i_{\mathrm{through}} = i$ . As a result, there is a magnetic field that circulates around each loop, and the circulation $\sum{B_{||}\Delta{\ell}} = \mu_0i_{\mathrm{through}}$ of the magnetic field is equal to $\mu_0i$ .