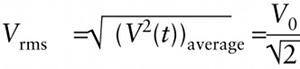Root mean square value (21-5)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

The root mean square (rms) value of \(V(t)\)...
Feedback
{"title":"The root mean square (rms) value of V(t)...","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,17,22,42\"}]"} {"title":"… is the square root of the average value of V sup 2 (t)","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"89,6,234,54\"}]"} {"title":"If V(t) is a sinusoidal function, its rms value equals the maximum value of V(t) (the amplitude) divided by the square root of 2","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"266,1,301,64\"}]"}

Review

As an example, in the United States the standard value for the ac voltage supplied by a wall socket is 120 V; this is actually the rms voltage, so \(V_{\mathrm{rms}} =\) 120 V. The voltage amplitude, or peak voltage, is larger by a factor of \(\sqrt{2}\), so \(V_0 = V_{\mathrm{rms}}\sqrt{2} = (120\ \mathrm{V})\ \sqrt{2} = 170\ \mathrm{V}\).

.