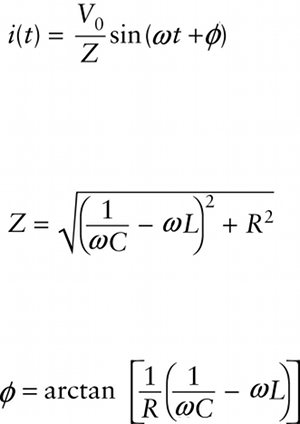Current in a driven LRC circuit (21-37)

Question 1 of 9

Question

Capacitance

{"title":"Current in a series LRC circuit","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"21,25,37,48\"}]"} {"title":"Amplitude of the voltage from the ac source","description":"Wrong","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"77,1,96,26\"}]"} {"title":"Phase of the current relative to the source voltage","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"204,22,222,52\"}]"} {"title":"Angular frequency of the source voltage and of the current","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"151,29,172,47\"}]"} {"title":"Impedance of the circuit","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"78,41,103,66\"},{\"shape\":\"rect\",\"coords\":\"6,209,29,234\"}]"} {"title":"Capacitance","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"109,229,130,253\"}]"} {"title":"Inductance","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"182,210,200,238\"}]"} {"title":"Resistance","description":"Incorrect","type":"incorrect","color":"#808000","code":"[{\"shape\":\"rect\",\"coords\":\"245,211,265,236\"}]"} {"title":"Phase of the current relative to the source voltage","description":"Incorrect","type":"incorrect","color":"#ff99cc","code":"[{\"shape\":\"rect\",\"coords\":\"1,381,18,410\"}]"}

Question

Current in a series $LRC$ circuit

{"title":"Current in a series LRC circuit","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"21,25,37,48\"}]"} {"title":"Amplitude of the voltage from the ac source","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"77,1,96,26\"}]"} {"title":"Phase of the current relative to the source voltage","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"204,22,222,52\"}]"} {"title":"Angular frequency of the source voltage and of the current","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"151,29,172,47\"}]"} {"title":"Impedance of the circuit","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"78,41,103,66\"},{\"shape\":\"rect\",\"coords\":\"6,209,29,234\"}]"} {"title":"Capacitance","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"109,229,130,253\"}]"} {"title":"Inductance","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"182,210,200,238\"}]"} {"title":"Resistance","description":"Incorrect","type":"incorrect","color":"#808000","code":"[{\"shape\":\"rect\",\"coords\":\"245,211,265,236\"}]"} {"title":"Phase of the current relative to the source voltage","description":"Incorrect","type":"incorrect","color":"#ff99cc","code":"[{\"shape\":\"rect\",\"coords\":\"1,381,18,410\"}]"}

Review

The first of Equations 21-37 shows that the greater the value of the impedance $Z$ , the smaller the amplitude $V_0/Z$ of the current. Like resistance, impedance has units of ohms. So you can think of it as similar to an “effective resistance” of the circuit to an ac current. Unlike resistance, however, impedance depends on the angular frequency as given by the second of Equations 21-37. The quantity $[1/ (\omega \mathrm{C}) - \omega L]^2$ is large at both low and high angular frequencies; that’s because the term $1/ (\omega \mathrm{C})$ (due to the capacitor) gets very large for low values of $\omega$ , while the term $\omega L$ (due to the inductor) gets very large for high values of $\omega$ . So the impedance $Z$ is large and the current amplitude $V_0/Z$ is small for very low angular frequencies thanks to the capacitor, as well as for very high angular frequencies thanks to the inductor. That’s just what we predicted above.