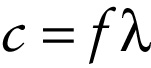Propagation speed, frequency, and wavelength of an electromagnetic wave (22-2)

Question 1 of 3

Question

Speed of light in a vacuum

{"title":"Speed of light in a vacuum","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,20,26,55\"}]"} {"title":"Frequency of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,7,119,66\"}]"} {"title":"Wavelength of the wave in vacuum","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"117,9,152,54\"}]"}

Review

Different kinds of electromagnetic waves have different frequencies and wavelengths. In Section 13-3 we learned that for a mechanical wave, the frequency $f$ and wavelength $\lambda$ are related to the propagation speed of the wave $v_{\mathrm{p}}$ by $v_{\mathrm{p}} = f\lambda$ (Equation 13-2). The same relationship holds for electromagnetic waves in a vacuum with $v_{\mathrm{p}}$ related by $c$ :

Equation 22-2 tells us that the product of frequency $f$ and wavelength $\lambda$ has the same value, $c$ , for all electromagnetic waves in a vacuum. The longer the wavelength, the lower the frequency; the shorter the wavelength, the higher the frequency.