Chapter 22. Intensity of an electromagnetic wave (22-25)

Question

delWIiL1WYDXKYqYxazM4k8LOJJpj2iCAY3g2CCsg9R5ARcq8aBWe4kQVeSMm8KyUzG9eEpovOA=

{"title":"Intensity of an electromagnetic wave","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Incorrect","type":"incorrect","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Question

bPc1Yg7xoR7yKjhmbmrt4oWiBz5cnkvqFSFY9UDw4ZQ=

{"title":"Intensity of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Correct!","type":"correct","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Incorrect","type":"incorrect","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Question

i7h9vvBqI98fS/1vo+YIVk412daDh4KghL20Sg==

{"title":"Intensity of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Wrong","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Incorrect","type":"incorrect","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Question

c5rMJ+SPmL5HoFBkbIrvNybqiLx+QiOn0hdOAWs9CMs=

{"title":"Intensity of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Incorrect","type":"incorrect","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Question

Ko+Bwd4cCS/72p2OLfE4zFk7NyTlqxu41y4kDw==

{"title":"Intensity of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Correct!","type":"correct","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Question

vBkI+Vt8MfnYrBL3sYTzTrVSmjHBcILzDs8PMOotkU0=

{"title":"Intensity of an electromagnetic wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,12,36\"}]"} {"title":"Speed of light in a vacuum","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"82,23,94,36\"},{\"shape\":\"rect\",\"coords\":\"161,7,172,21\"}]"} {"title":"Magnetic field rms value","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"171,1,181,19\"}]"} {"title":"Permeability of free space","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"255,32,273,48\"},{\"shape\":\"rect\",\"coords\":\"169,31,187,49\"}]"} {"title":"Electric field rms value","description":"Incorrect","type":"incorrect","color":"#ff6600","code":"[{\"shape\":\"rect\",\"coords\":\"109,16,123,36\"}]"} {"title":"Permittivity of free space","description":"Correct!","type":"correct","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"95,19,105,38\"}]"}

Review

An even more useful way to express the energy carried by an electromagnetic wave is in terms of the wave intensity, or average power per unit area. Figure 22-12 shows a portion of a wave that has cross-sectional area \(A\) and length \(\ell\). The energy in this portion of the wave is \(u_{\mathrm{average}}\) from Equation 22-24 multiplied by the volume \(A\ell\) of this portion. This entire portion of the wave moves at speed \(c\) through the cross-sectional area \(A\) in a time \(t\). The power equals the energy in the wave portion divided by the time \(t = \ell/c\) that it takes this portion of the wave to travel at speed c through the crosssectional area \(A\). The intensity, to which we give the symbol \(S_{\mathrm{average}}\), equals the power divided by the area \(A\). So

\(S_{\mathrm{average}}= \frac{\mathrm{energy}}{\mathrm{time}} \times \frac{1}{\mathrm{area}} = \frac{(u_{\mathrm{average}}A \ell)}{\ell /c} \times \frac{1}{A} = u_{\mathrm{average}}c\)

Using Equation 22-24, we can rewrite this as

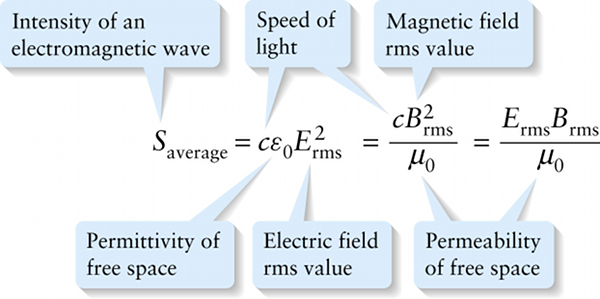
(To write the last expression in Equation 22-25, we used the result that since \(B_0 = E_0/c\), it follows that \(B_{\mathrm{rms}} = E_{\mathrm{rms}}/c\).)