Chapter 28. Energy of a photon (22-26)

Review

To see how it’s possible to violate energy conservation, let’s consider the photon. We learned in Section 22-4 that the energy of a photon is proportional to its frequency:

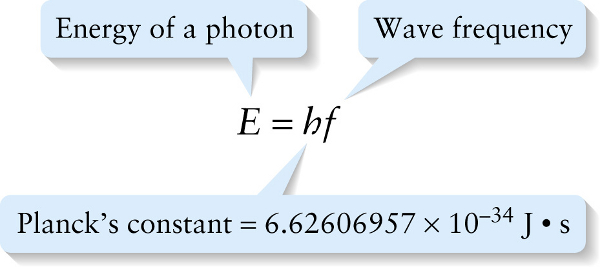
For a photon to have a definite energy, it must therefore have a definite frequency. However, a wave \(\psi\) with a definite frequency also has an infinite duration (Figure 28 5a). This means that wave has always been present and will always be present. A more realistic description of a wave is one that has a finite duration: for example, the wave produced when you turn a source of waves (like a laser pointer) on and then off again. Mathematically, a wave of a finite duration \(\Delta{t}\) can be expressed as a sum of waves of infinite duration like the one shown in Figure 28-5a, but with a range of frequencies of breadth \(\Delta{f}\) (Figure 28-5b). To make a shorter-duration wave, we have to add together infinite-duration waves from a broader range of frequencies (Figure 28-5c).