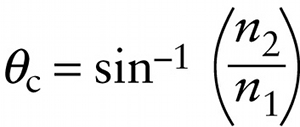Chapter 23. Critical angle for total internal reflection (23-10)

Review

We can calculate the critical angle \(\theta_{\mathrm{c}}\) using Snell’s law of refraction, Equation 23-6.When the incident angle \(\theta_1\) equals the critical angle \(\theta_{\mathrm{c}}\), the refracted angle \(\theta_2\) equals 90°.If we substitute these into Equation 23-6 and recall that sin 90° = 1, we get

(23-9) \(n_1 \sin{\theta_{\mathrm{c}}} = n_2 \sin{90^{\circ}} = n_2\ \mathrm{so}\ \sin{\theta_{\mathrm{c}}} = \frac{n_2}{n_1}\)

Note that the sine of an angle between 0 and 90° is between 0 and 1. If \(n_1 > n_2\), the ratio \(n_2/n_1\) is less than 1, and there will be some angle \(\theta_{\mathrm{c}}\) for which Equation 23-9 issatisfied. In this case total internal reflection is possible. But if \(n_1 < n_2\), the ratio \(n_2/n_1\) isgreater than 1 and Equation 23-9 has no solution. This is another way of seeing thattotal internal reflection is possible only if \(n_1 > n_2\).

If we solve Equation 23-9 for the critical angle \(\theta_{\mathrm{c}}\), we get