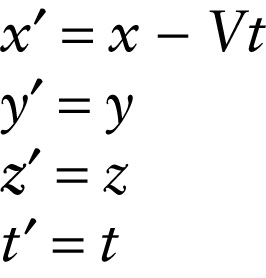Galilean coordinate transformation (25-1)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

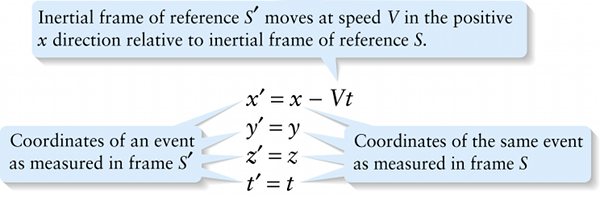
Inertial frame of reference \(\boldsymbol{S}′\) moves at speed \(\boldsymbol{V}\) in the positive \(\boldsymbol{x}\) direction relative to inertial frame of reference \(\boldsymbol{S}\)
Feedback
{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"207,2,249,55\"}]"} {"title":"Coordinates of the same event as measured in frame S","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"107,18,142,57\"},{\"shape\":\"rect\",\"coords\":\"103,86,138,139\"},{\"shape\":\"rect\",\"coords\":\"101,161,136,201\"},{\"shape\":\"rect\",\"coords\":\"96,226,124,265\"}]"} {"title":"Coordinates of an event as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,34,56\"},{\"shape\":\"rect\",\"coords\":\"1,92,33,137\"},{\"shape\":\"rect\",\"coords\":\"2,158,28,197\"},{\"shape\":\"rect\",\"coords\":\"1,226,23,265\"}]"}

Review

This set of equations is known as the Galilean transformation. Note that the relative motion of the two frames of reference along the positive \(x\) axis does not impact the measured values of the \(y\) and \(z\) components, which are the same in both reference frames.