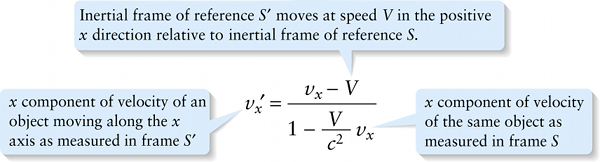
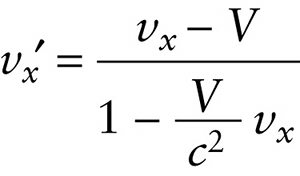Lorentz velocity transformation (25-17)
Question
\(x\) component of velocity of an object moving along the \(x\) axis as measured in frame \(S′\)
{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"226,5,261,46\"}]"} {"title":"x component of velocity of the same object as measured in frame S","description":"Wrong","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"249,107,278,138\"}]"} {"title":"x component of velocity of an object moving along the x axis as measured in frame S′","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,48,24,77\"}]"}Review
This is called the Lorentz velocity transformation. Notice that if the speed \(V\) of one frame relative to the other is small compared to \(c\), the ratio \(V/c\) is much less than 1 and the denominator is essentially equal to 1. Then Equation 25-17 becomes \(v_x' = v_x- V\), which is just the Galilean velocity transformation (the first of Equations 25-5). The same thing happens if the velocity \(v_x\) of the object relative to frame \(S\) is small compared to \(c\). So if either of the speeds involved is a small fraction of the speed of light, the Lorentz velocity transformation reduces to the Galilean velocity transformation. This justifies our use of the Galilean velocity transformation for slow-moving objects.