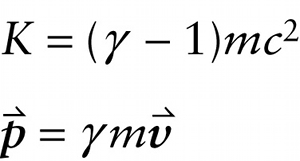Einsteinian expressions for kinetic energy and momentum (25-20)

Question 1 of 3

Question

Momentum of a particle of mass $m$ and velocity vector $\vec{v}$

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,16,38,60\"}]"} {"title":"Relativistic gamma for speed v","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,26,131,66\"},{\"shape\":\"rect\",\"coords\":\"78,120,109,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,122,24,162\"}]"}

Question

Relativistic gamma for speed $v$

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,16,38,60\"}]"} {"title":"Relativistic gamma for speed v","description":"Correct!","type":"correct","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,26,131,66\"},{\"shape\":\"rect\",\"coords\":\"78,120,109,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,122,24,162\"}]"}

Question

Kinetic energy of a particle of mass $m$ and velocity $\vec{v}$

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,16,38,60\"}]"} {"title":"Relativistic gamma for speed v","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"102,26,131,66\"},{\"shape\":\"rect\",\"coords\":\"78,120,109,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,122,24,162\"}]"}

Review

The dimensionless quantity in Equation 25-19 is equal to 1 when $v = 0$ and becomes infinitely large as $v$ approaches $c$ (Figure 25-13). In terms of relativistic gamma, we can write the correct expressions for kinetic energy and momentum as