Chapter 26. Einsteinian expressions for kinetic energy and momentum (25-20)

Question

q1DLq9FCM5NE+JheWqnv4iyNEScYQRErq0bdd/7WJnDY7TtI/akUExBL3SYJcYjHjjnEKrYkX8WP8VnKzm6sVAApmD1TXDmpVlsgjXmPm8yqB80X4k1uEg==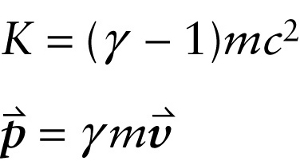

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,35,59\"}]"} {"title":"Relativistic gamma for speed v","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"99,27,134,66\"},{\"shape\":\"rect\",\"coords\":\"76,118,110,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,117,28,162\"}]"}

Question

SsRmYhQtG5z5x9KP3YJv36uSRj/w/q+9yqBvm39pjPjGAnYz6+yePMNM6DR37TY1OaLdYHNH+YU=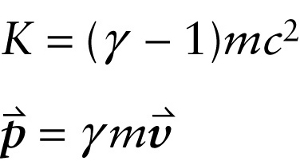

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,35,59\"}]"} {"title":"Relativistic gamma for speed v","description":"Correct!","type":"correct","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"99,27,134,66\"},{\"shape\":\"rect\",\"coords\":\"76,118,110,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,117,28,162\"}]"}

Question

i+1GF8NSeD1/k+O0Koq59ChGYC3Wr0ZZP2jCyMX+qVk+uuJM1OFUTsXq8tfVBRE2tgBtKs0AyP3YbFoUSYVO6xRrEQonFTpIOgw1u93zMwbFWah0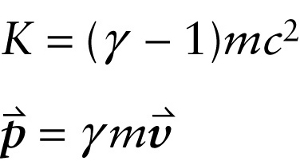

{"title":"Kinetic energy of a particle of mass m and velocity vector v","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,35,59\"}]"} {"title":"Relativistic gamma for speed v","description":"Wrong","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"99,27,134,66\"},{\"shape\":\"rect\",\"coords\":\"76,118,110,159\"}]"} {"title":"Momentum of a particle of mass m and velocity vector v","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,117,28,162\"}]"}

Review

Blackbody radiation and the photoelectric effect suggest that photons can be treated like tiny bundles. We have therefore made the claim that as quantized units of energy, photons have a particle-like nature. Are there other implications of this claim? For example, an electron absorbs the energy of a photon in the photoelectric effect. But if a photon is like a particle, is it possible that, as in the collisions we studied in Chapter 7, a photon could strike an electron and bounce off? If so, based on our experience with collisions, we ought to expect that linear momentum would be conserved in such an interaction and that the momentum of the photon should change as a result. This effect, called Compton scattering, is further evidence that light does indeed come in the form of photons.

Let’s first see how to express the momentum of a photon. We saw in Section 25-7 that for a particle of mass \(m\), we can write the kinetic energy and momentum as