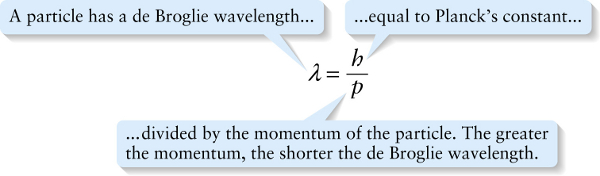
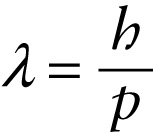de Broglie wavelength (26-10)
Question
...divided by the momentum of the particle. The greater the momentum, the shorter the de Broglie wavelength.
{"title":"A particle has a de Broglie wavelength...","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,37,38,92\"}]"} {"title":"...equal to Planck’s constant...","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"109,4,141,52\"}]"} {"title":"...divided by the momentum of the particle. The greater the momentum, the shorter the de Broglie wavelength.","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"108,82,143,133\"}]"}Review
We have seen that light, previously thought to be a wave, is actually a stream of particles. But these particles (photons) have a wave aspect: Associated with them is a frequency \(f\), which determines the photon energy \(E = hf\), and a wavelength \(\lambda\), which determines the photon momentum \(p = h/\lambda\). So light has a dual nature, with attributes of both wave and particle. Is it possible that the same could be true for ordinary matter, which we know is made of particles such as electrons, protons, and neutrons? Could these particles also have a wave aspect?
In 1924, French graduate student Louis de Broglie (pronounced “de broy’”) proposed precisely that idea. In particular, he suggested that the relationship \(p = h/\lambda\) between momentum \(p\) and wavelength \(\lambda\) that applies to photons should also apply toparticles such as electrons (Figure 26-9). The wavelength of a particle is called its de Broglie wavelength: