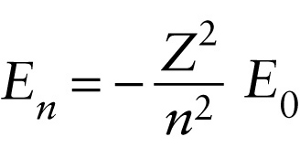Electron energies in the Bohr model (26-27)
Question 1 of 4
Question
Rydberg energy = 13.6 eV
{"title":"Electron energy for the nth allowed orbit in a single-electron atom","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,56,37,104\"}]"} {"title":"Atomic number of the atom","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"159,27,200,78\"}]"} {"title":"Rydberg energy = 13.6 eV","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"242,56,280,102\"}]"} {"title":"n = 1, 2, 3, ...","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"161,109,196,138\"}]"}
Review
Using Equation 26-26, we can write Equation 26-25 for the quantized electron orbital energy in terms of the Rydberg energy E0:
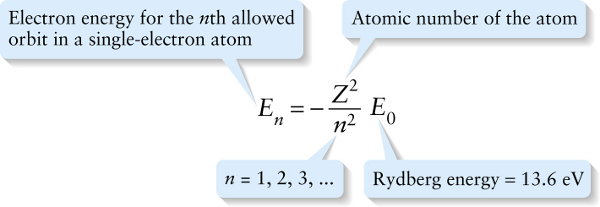
Again, the integer n identifies the orbit, and the atomic number Z specifies a particular element. Setting Z equal to 1 and n equal to 1 therefore tells us that the energy of the ground state of hydrogen is −13.6 eV. We can also conclude from Equation 26-27 together with the value of the Rydberg energy that, in general, the energy of electrons in orbit around an atomic nucleus is between about −10 eV and, for the largest elements (for which Z is about 100), −105 eV. The Bohr model sets the scale for atomic electron energies.