Chapter 27. Binding energy of a nucleus (27-2)

Review

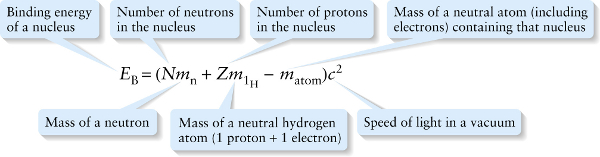
To find the binding energy of \(\sideset{^4}{\mathrm{He}}{}\), we subtracted the mass of the nucleus from the mass of the two protons and two neutrons separately, and then multiplied by \(c^2\) to find the equivalent energy. In general, for a nucleus consisting of \(N\) neutrons and \(Z\)protons, \(E_{\mathrm{B}}\) is

\(E_{\mathrm{B}} =\left(N m_{\mathrm{n}} + Zm_{\mathrm{p}} - m_{\mathrm{nucleus}}\right)c^2\)

where \(m_{\mathrm{n}}\) is the mass of a neutron, \(m_{\mathrm{p}}\) is the mass of a proton, and \(m_{\mathrm{nucleus}}\) is the mass of the nucleus. In practice, it’s easier to measure the masses of neutral atoms (including their electrons) than the masses of isolated atomic nuclei. In terms of these masses, we can write the binding energy of a nucleus as