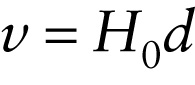The Hubble law (28-9)

Question 1 of 3

Question

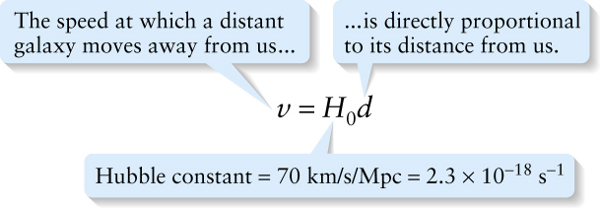
Hubble constant = 70 km/s/Mpc = $2.3 \times 10^{−18}\mathrm{s}^{-1}$

{"title":"The speed at which a distant galaxy moves away from us...","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,18,30,56\"}]"} {"title":"...is directly proportional to its distance from us.","description":"Wrong","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"166,7,194,54\"}]"} {"title":"Hubble constant = 70 km/s/Mpc = 2.3 × 10 sup −18 s sup −1","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"93,9,142,56\"}]"}

Review

This direct proportionality is called the Hubble law, and the constant $H_0$ in Equation 28-9 is called the Hubble constant. Astronomers typically measure distances in the cosmos in parsecs (pc), a unit equal to 3.26 light-years. One light-year (ly) is the distance that light travels in one year, equal to $3.09 \times 10^{16} \mathrm{m}$ . The current best value of $H_0$ is about 70 km $/\ \mathrm{s}\ /\$ Mpc, where 1 Mpc = 1 megaparsec = $10^6\ \mathrm{pc} = 3.26 \times 10^6$ ly.