A-1

Astronomy is a science of extremes. As we examine various cosmic environments, we find an astonishing range of conditions—from the incredibly hot, dense centers of stars to the frigid, near-perfect vacuum of interstellar space. To describe such divergent conditions accurately, we need a wide range of both large and small numbers. Astronomers avoid such confusing terms as “a million billion billion” (1,000,000,000,000,000,000,000,000) by using a standard shorthand system. All the cumbersome zeros that accompany such a large number are consolidated into one term consisting of 10 followed by an exponent, which is written as a superscript and called the power of ten. The exponent merely indicates how many zeros you would need to write out the long form of the number. Thus,

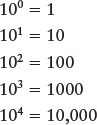
and so forth. Equivalently, the exponent tells you how many tens must be multiplied together to yield the desired number. For example, ten thousand can be written as 10⁴ (“ten to the fourth”) because 10⁴ = 10 × 10 × 10 × 10 = 10,000. Similarly, 273,000,000 can be written as 2.73 × 10⁸.

In scientific notation, numbers are written as a figure between 1 and 10 multiplied by the appropriate power of 10. The distance between Earth and the Sun, for example, can be written as 1.5 × 10⁸ km (or 9.3 × 10⁷ mi). Once you get used to it, you will find this notation more convenient than writing “150,000,000 kilometers” or “one hundred and fifty million kilometers.”

This powers-of-ten system can also be applied to numbers that are less than 1 by using a minus sign in front of the exponent. A negative exponent tells you that the location of the decimal point is as follows:

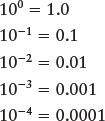
and so forth. For example, the diameter of a hydrogen atom is approximately 1.1 × 10⁻⁸ cm or (4.3 × 10⁻⁹ in). That is more convenient than saying “0.000000011 centimeter,” “11 billionths of a centimeter,” or the equivalent numbers in U.S. customary units. Similarly, 0.000728 equals 7.28 × 10⁻⁴.

Using the powers-of-ten shorthand, one can write large or small numbers like these compactly:

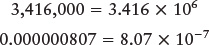
Because powers-of-ten notation bypasses all the cumbersome zeros, a wide range of circumstances can be numerically described conveniently:

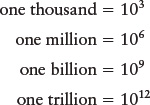
and also

Try these questions: Write 3,141,000,000 and 0.0000000031831 in scientific notation. Write 2.718282 × 10¹⁰ and 3.67879 × 10⁻¹¹ in standard notation.

(Answers appear at the end of the book.)

APPENDIX B: TEMPERATURE SCALES

Three temperature scales are in common use. Throughout most of the world, temperatures are expressed in degrees Celsius (°C), named in honor of the Swedish astronomer Anders Celsius, who proposed it in 1742. The Celsius temperature scale (also known as the “centigrade scale”) is based on the behavior of water, which freezes at 0°C and boils at 100°C at sea level on Earth.

Scientists usually prefer the Kelvin scale, named after the British physicist Lord Kelvin (William Thomson), who made many important contributions to our knowledge about heat and temperature. On the Kelvin temperature scale, water freezes at 273 K and boils at 373 K. Note that we do not use the degree symbol with the Kelvin temperature scale.

A-2

Because water must be heated by 100 K or 100°C to go from its freezing point to its boiling point, you can see that the size of a kelvin is the same as the size of a degree Celsius. When considering temperature changes, measurements in kelvins and in degrees Celsius lead to the same number.

A temperature expressed in kelvins is always equal to the temperature in degrees Celsius plus 273. Scientists prefer the Kelvin scale because it is closely related to the physical meaning of temperature. All substances are made of atoms, which are very tiny (a typical atom has a diameter of about 10⁻¹⁰ m or 3.9 × 10⁻⁹ in) and constantly in motion. The temperature of a substance is directly related to the average speed of its atoms. If something is hot, its atoms are moving at high speeds. If a substance is cold, its atoms are moving much more slowly.

The coldest possible temperature is the temperature at which atoms move as slowly as possible (they can never quite stop completely). This minimum possible temperature, called absolute zero, is the starting point for the Kelvin scale. Absolute zero is 0 K, or −273°C. Because it is impossible for anything to be colder than 0 K, there are no negative temperatures on the Kelvin scale.

In the United States, many people still use the now outdated Fahrenheit scale, which expresses temperature in degrees Fahrenheit (°F). When the German physicist Gabriel Fahrenheit introduced this scale in the early 1700s, he intended 0°F to represent the coldest temperature then achievable (with a mixture of ice and saltwater) and 100°F to represent the temperature of a healthy human body. On the Fahrenheit scale, water freezes at 32°F and boils at 212°F. Because there are 180 degrees Fahrenheit between the freezing and boiling points of water, a degree Fahrenheit is only 100/180 (= 5/9) the size of the other scales.

The following equation converts from degrees Fahrenheit to degrees Celsius:

T_C = 5/9 (T_F − 32)

To convert from Celsius to Fahrenheit, a simple rearrangement of terms gives the relationship

T_F = 9/5 T_C + 32

where T_F is the temperature in degrees Fahrenheit and T_C is the temperature in degrees Celsius.

For example, consider a typical room temperature of 68°F. Using the first equation, we can convert this measurement to the Celsius scale as follows:

T_C = 5/9 (68 − 32) = 20°C

To arrive at the Kelvin scale, we simply add 273 degrees to the value in degrees Celsius. Thus, 68°F = 20°C = 293 K. Figure B-1 displays the relationships among these three temperature scales.

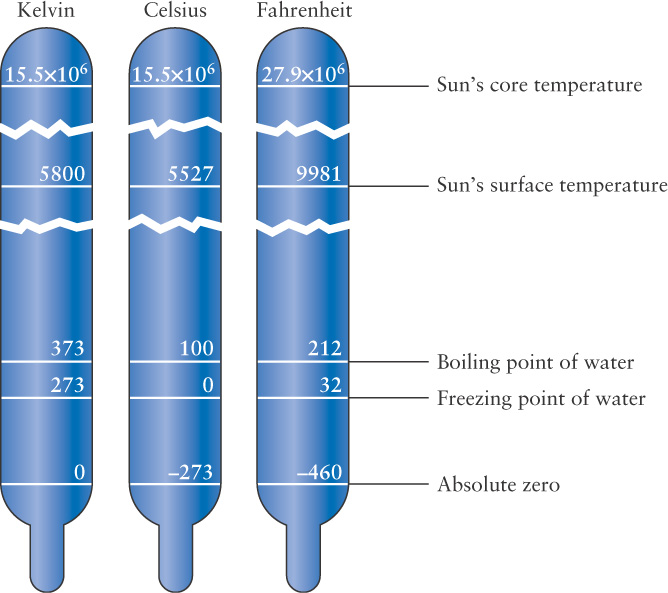
Try these questions: The Sun’s surface temperature is about 5800 K. What is its temperature in Celsius and Fahrenheit? The temperature of empty space is about 3 K. What is its temperature in Celsius and Fahrenheit? (Answers appear at the end of the book.)

A-3

* For Jupiter, Saturn, Uranus, and Neptune, the internal rotation period is given. A superscript R means that the rotation is retrograde (opposite the planet’s orbital motion).

A-4

*A superscript R means that the satellite orbits in a retrograde direction (opposite to the planet’s rotation).

A-5

*Stars that are components of binary systems are labeled A and B.

**A positive radial velocity means the star is receding; a negative radial velocity means the star is approaching.

Compiled from the Hipparcos General Catalogue and from data reported by the Research Consortium on Nearby Stars. The table lists all known stars within 4.00 parsecs (13.05 light-years).

A-6

Data in this table compiled from the Hipparcos General Catalogue.

*A positive radial velocity means the star is receding; a negative radial velocity means the star is approaching.

**This is the ratio of the star’s apparent brightness to that of Sirius, the brightest star in the night sky.

Note: Acrux, or α Cru (the brightest star in Crux, the Southern Cross), appears to the naked eye as a star of apparent magnitude +0.87, the same as Aldebaran, but it does not appear in this table because Acrux is actually a binary star system. The blue-white component stars of this binary system have apparent magnitudes of +1.4 and +1.9; thus, they are dimmer than any of the stars listed here.

A-7

^*Genitive is the grammatical case denoting possession. For example, astronomers denote the brightest or α (alpha) star in Orion (Betelgeuse) as α Orionis.

¹Constellations of the area of the sky known as the wet quarter for its many watery images.

²A zodiac constellation.

³Sometimes considered as Sagittarius’s crown.

⁴Ariadne’s crown.

⁵Corvus was Orpheus’s companion, Lyra his harp.

⁶Originally a part of Centaurus.

⁷Contains the Large Magellanic Cloud and the south ecliptic pole.

⁸Contains the north ecliptic pole.

⁹One of the oldest constellations known.

¹⁰Originally the claws of Scorpius.

¹¹Originally named Musca Australis to distinguish it from Musca Borealis, the northern fly, which is now defunct; “Australis” is now dropped.

¹²Contains the south celestial pole.

¹³Ophiucus is identified with the physician Aesculapius, and Serpens with the caduceus.

¹⁴Contains the galactic center.

¹⁵Originally named by Lacaille l’Atelier du Sculpteur (in Latin, Apparatus Sculptoris); now known simply as Sculptor. Contains the south galactic pole.

¹⁶Shield of the Polish hero John Sobieski.

¹⁷Contains the Small Magellanic Cloud.

¹⁸Contains the north celestial pole.

A-8

A-9

A-10

A-11

*The numbers after the plus or minus (±) symbol indicate the possible errors in the given numbers.

This table lists the major contributions to the mass and energy of the universe.

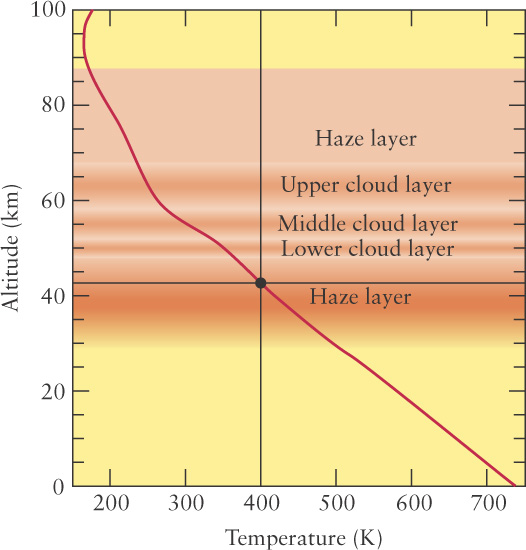
The graphs you will encounter in this book are compact ways of displaying patterns of information relating two variables, like the temperature and luminosity of stars or the temperature of an atmosphere at different altitudes. The relevant values of one of the variables are presented along the horizontal or x axis, and the relevant values of the other variable are presented along the vertical or y axis. The word “relevant” here indicates that often graphs do not start at 0. Consider three examples. First is data presented in Chapter 6 concerning the temperature of Venus’s atmosphere at different altitudes (Figure M-1).

A-12

The horizontal axis of the graph indicates the temperature in kelvins (K). (Unlike degrees Celsius or degrees Fahrenheit, temperature using the Kelvin scale is simply noted as kelvins.)

The vertical axis denotes the altitude above Venus’s surface in kilometers (km). Note that both axes are always labeled with a name (temperature or altitude, here) and units (K or km, respectively). Bear in mind that some variables in graphs you will see in this book increase to the right or upward (these are more common), but some variables will increase in the opposite directions. To read a graph, note that a value on the horizontal axis is transferred directly upward through the graph. For example, all points on the blue line in Figure M-1 (which extends upward from 400 K) have a temperature of 400 K. Equivalently, the value given on the vertical axis is transferred to all points horizontally across from this value. All the points on the black line in Figure M-1 are at an altitude of about 43 km above Venus’s surface. We have interpolated between 40 and 45 to get this value (Figure M-2).

A curve or a set of points on the graph presents the relationship between the variable represented on the horizontal axis and the variable on the vertical axis. Each point on a curve or each separate point relates the two variables. Choose a point, say, the dot on Figure M-1. It represents the temperature at a certain altitude above Venus’s surface. To find the temperature at that point, you slide directly down (along the blue line in this example) from the point and read the value of the horizontal variable under it. To find the altitude for that point, you slide directly over to the side (along the black line) and read the value of the vertical variable there. In our example, sliding along the blue line leads to 400 K on the temperature line. Therefore, this point corresponds to a temperature of 400 K. Moving horizontally from the point, you encounter, by interpolation, the 43 km indicator. Combining the data, you conclude that the temperature of Venus’s atmosphere 43 km above its surface is 400 K.

The red curve in Figure M-1 provides the relationship between altitude and temperature for a wide range of locations above Venus in a representation that is much more informative than a table of heights and temperatures. Specifically, this curve shows you the trend of temperature with altitude.

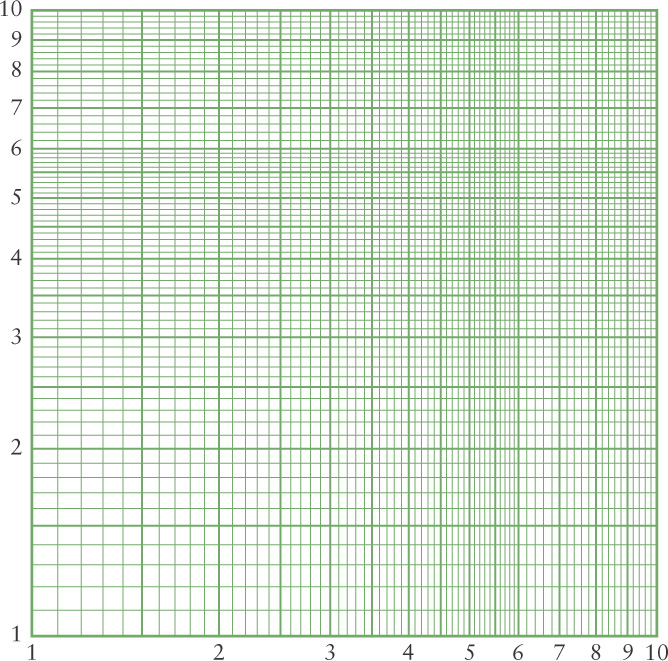
Try these questions: What is the temperature at 20 km? What is the altitude at which the temperature is 300 K? For most of this graph, what is the general trend of the temperature with height? (Answers appear at the end of the book.)

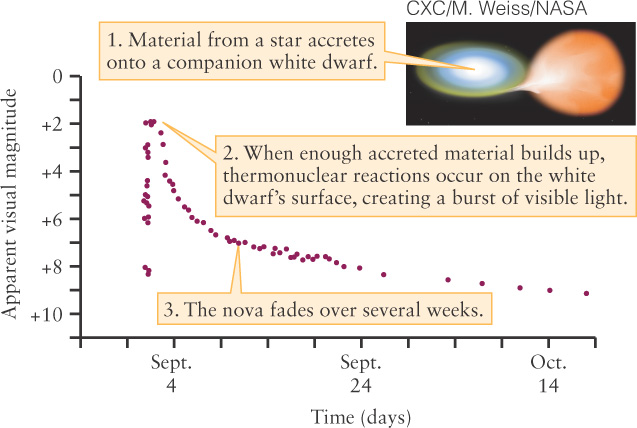
Sometimes, the known information is not a curve, but rather a set of points, as in our second example (Figure M-3) from Chapter 12. In this case, the graph connects the apparent magnitude of a nova (how bright it appears to be as seen from Earth regardless of its distance or other factors) and time. Each dot indicates how bright the nova (an explosion on the surface of certain stars) was at different times. For example, the peak brightness of the nova was an apparent magnitude of about +2 and it occurred on September 2. Noting that time passes to the right, you can immediately see that the trend of the nova’s brightness is to increase rapidly and decrease more slowly.

Try these questions: What is the apparent magnitude on September 24? October 9? On what two days was the apparent magnitude +6? (Answers appear at the end of the book.)

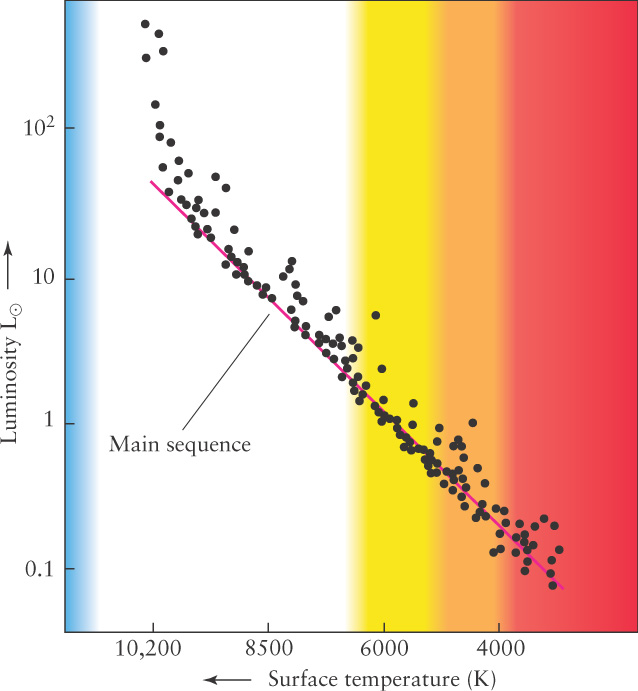
The graphs so far have shown variables that change uniformly along the axes. For example, the distance on Figure M-1 from 300 K to 400 K is the same as the distance from 400 K to 500 K, and so on. Many graphs you will encounter have variables that do not change uniformly (that is, linearly) along the axes. That means that the change in value going along each axis varies—there is not the same amount of change per centimeter or inch along the axis. In Figure M-4, from Chapter 11, for example, the luminosity (total energy emitted per second) increases upward logarithmically, while the temperature decreases going from left to right in a more complex, nonuniform way.

A-13

The purpose of logarithmic and other nonlinear axes is to present in compact form data that vary very widely in values. For example, the dimmest star represented in Figure M-4 is just less than 0.1 times as luminous as the Sun, while the brightest star is nearly 1000 times as luminous. The process of getting information from logarithmic graphs is the same as linear graphs. You must just be careful not to think of values as doubling or tripling when you go over or up two or three intervals. Figure M-5 shows how a logarithmic scale varies over one decade of values on both the vertical and horizontal axes. The same numbering intervals apply for any decade of values, for example, 1 to 10 or 10⁵ to 10⁶. As you can see, the numbers bunch up near the highest value, so you need to interpolate these graphs more carefully than linear graphs.

Referring to Figure M-4, the luminosity of a star with surface temperature of 4000 K is about 0.1 L_⊙. Note, also, that some graphs are linear on one axis and logarithmic on the other axis!

Try these questions: Approximately what is the luminosity of a star with surface temperature 8500 K? What is the surface temperature of a star with the same luminosity as the Sun (1 L_⊙)?

(Answers appear at the end of the book.)

A-14

A-15

Tides result from a combination of Earth’s motion around its barycenter with the Moon (or Sun) and the changing strength of the gravitational force from the Moon (or Sun) across Earth. Ignoring Earth’s rotation and focusing on the Moon for the moment, let’s first consider the motion of Earth and the Moon around their barycenter (see Figure 6-31a). The barycenter is located 1720 km (1068 mi) below Earth’s surface on the line between the centers of Earth and the Moon. As a result of its motion around the barycenter, every point on Earth feels an equally strong force away from the Moon, unlike the outward force that you feel while riding on a merry-go-round, which increases with distance from the center. The force away from the Moon is represented at three locations by the force labeled F_out in Figure O-1a.

Opposing this force away from the Moon, Earth also has a gravitational attraction to its satellite. Recall from Section 2-8 on Newton’s law of gravitation that the gravitational force exerted by one body on another decreases with distance. Therefore, the Moon’s gravitational attraction on Earth is greatest at the point on Earth’s surface closest to the Moon. This attraction is greater than the force felt at the center of Earth, which in turn is greater than the force felt on the opposite side of Earth from the Moon. The gravitational force in these places is labeled F_grav in Figure O-1a.

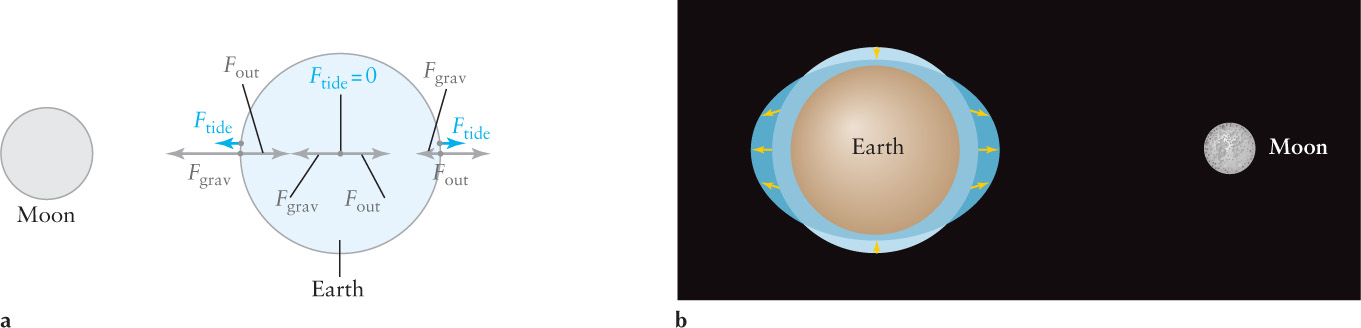
Because forces in the same or opposite directions simply add or subtract, respectively, we can subtract the two forces F_out and F_grav at any point on Earth, due to the presence of the Moon. The resulting net force is labeled F_tide in Figure O-1a and is the tidal force acting at these places. For example, at the point on Earth directly below the Moon, the tidal force is very strong and points toward the Moon. At the center of Earth, the two forces cancel each other completely. At the point on the opposite side of Earth from the Moon, the tidal force is equal in strength to the tidal force directly under the Moon but is directed away from the Moon.

Consider the point on Earth closest to the Moon. The strength of the tidal force, F_tide, seems to imply that the Moon’s gravitational force lifts the water there to create the high tide. However, the force of gravitation from the Moon is not strong enough to raise that water more than a few centimeters or inches. Rather, the high tide closest to the Moon occurs because ocean waters from nearly halfway around to the opposite side of Earth are pulled Moonward by the gravitational force acting on them. This water slides toward the Moon and fills the ocean directly under it, creating a tidal bulge or high tide. Likewise, the net outward force acting on the opposite side of Earth from the Moon pushes the waters that are just over halfway around from the Moon to the side directly away from it, creating a simultaneous second high tide of equal magnitude on the opposite side of Earth from the Moon. Where the water has been drained away in this process, low tides occur.

Let’s spin Earth back up. As it rotates, the geographic locations of the high and low tides continually change. Figure O-1b indicates that high tides occur when the Moon is high in the sky or below our feet, while low tides occur when the Moon is near either horizon. This timing means that there are two cycles of high and low tides at most places on Earth each day. These cycles do not span exactly 24 hours, however, because the Moon is moving along the celestial sphere, changing the time at which high or low tide occurs at any location from day to day. As a result, the time between consecutive high tides is 12 hours, 25 minutes.

Tides are complicated by the fact that the oceans are not uniformly deep, and the shores around continents and islands have a variety of shapes. As a result, in some places the oceans have only a single cycle of tides each day. Some places have tides that change negligibly, while some channels, such as the Bay of Fundy between the United States and Canada (maximum range between high and low tides of 16.3 m or 17.8 yd) and the Bristol Channel between Wales and England (maximum range of 15 m or 16.4 yd), have two tides that are each much higher than normal.

A-16

Earth’s rotation also has the effect of moving the high tides away from the line between the centers of Earth and the Moon. Earth’s eastward rotation is nearly 30 times faster than the Moon’s eastward revolution around Earth. Therefore, as it rotates, Earth drags the high tides eastward with it. As a result, the high tide that should be directly between the centers of Earth and the Moon is actually 10° ahead of the Moon in its orbit around Earth (Figure O-2). This high tide stays at roughly this position because the Moon’s gravitational force pulls the tide westward while it is being dragged eastward by Earth’s rotation; the two effects balance each other out. A similar argument applies to the tide on the opposite side of Earth.

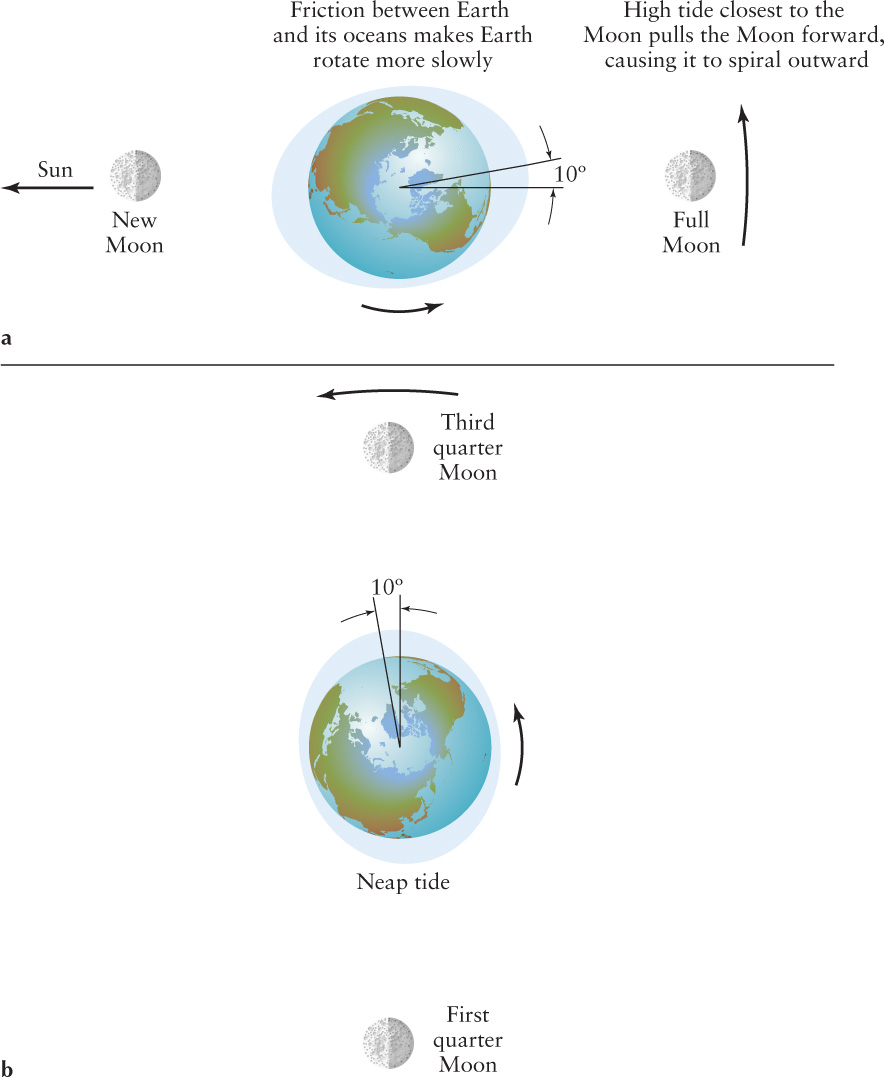
We can repeat this analysis for the Earth–Sun system and get the same qualitative results.

Scientists identify two types of energy that are available to any object. The first, called kinetic energy, is associated with the object’s motion. For speeds much less than the speed of light, we can write the amount of kinetic energy, KE, of an object as

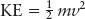
where m is the object’s mass and v is its speed. Kinetic energy is a measure of how much work the object can do on the outside world or, equivalently, how much work the outside world has done to give the object this speed. Kinetic energy applies to rotation and revolution, as well as to straight-line motion.

Work is also a rigorously defined concept that often is at odds with our intuition. Work is defined as the product of the force, F, acting on an object and the distance, d, over which the object moves in the direction of the force:

W = Fd

For example, if I exert a horizontal force of 50 N (N is the unit newtons and is the metric unit of force) and thereby move an object 10 m in the direction I push it, then I have done 50 N × 10 m = 500 J of work. (I have used the relationship that 1 newton × 1 meter = 1 joule.)

The second type of energy is called potential energy, the energy available to an object as a result of its location in space. For example, if you hold a pencil above the ground, the pencil has potential energy that can be converted into kinetic energy by Earth’s gravitational force. How does that conversion get underway? Just let go of the pencil.

There are various kinds of potential energy, such as the potential energy stored in a battery and the potential energy stored in objects under the influence of gravity. We will focus on gravitational potential energy. Far from extremely massive objects, like stars, or extremely dense objects, like black holes, gravitational potential energy, PE, can be written as

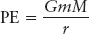
where the constant G = 6.6683 × 10⁻¹¹ N m²/kg², m is the mass of the object whose gravitational potential energy you are measuring, M is the mass of the object generating the gravitational attraction, and r is the distance between the centers of mass of these two objects.

Near the surface of Earth, this equation simplifies to

PE = mgh

A-17

where g = 9.8 m/s² (32 ft/s²) is the gravitational acceleration at Earth’s surface, and h is the height of the object above Earth’s surface.

Potential energy can be converted into kinetic energy and vice versa. After you drop a pencil, its gravitational potential energy begins to decrease while its kinetic energy begins to increase at the same rate. The pencil’s total energy is conserved. Conversely, if you throw a pencil up in the air, the kinetic energy you give it will immediately begin to decrease, while its potential energy increases at the same rate.

Related to the motion of an object and, hence, to its kinetic energy are the concepts of linear momentum, usually just called momentum, and angular momentum. Momentum, p, is described by the equation

p = mv

where v is the velocity of the object. Both p and v are in boldface to indicate that they both represent motion in some direction or another (both in the same direction), as well as a numeric value. Simple algebra reveals that kinetic energy and momentum are related by

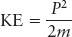
Linear momentum, then, indicates how much energy is available to an object because of its motion in a straight line (linear motion).

Angular momentum, L, can be expressed mathematically as

L = Iω

where I is the moment of inertia of an object, and ω (lowercase Greek omega) is the angular speed and direction of the rotating object. Just as an object’s mass indicates how hard it is to change an object’s straight-line motion, the moment of inertia indicates how hard it is to change the rate at which an object rotates or revolves. The moment of inertia depends on an object’s mass and shape. Kinetic energy due to angular motion can be written as

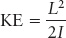
Newton’s first law can also be expressed in terms of conservation of linear momentum:

A body maintains its linear momentum unless acted upon by a net external force.

Equivalently, for angular motion we can write the conservation of angular momentum:

A body maintains its angular momentum unless acted upon by a net external torque.

Torques are created when a force acts on an object in some direction other than toward the center of the object’s angular motion, as shown in Figure P-1.

Earth has angular momentum from two sources, namely, from spinning on its rotation axis and from orbiting the Sun. Likewise, the Moon has angular momentum because it spins on its rotation axis and it orbits Earth. Virtually all objects in astronomy have angular momentum, and it is probably fair to say that conservation of angular momentum is among the most important laws in the cosmos. After all, conservation of angular momentum is what keeps the planets in orbit around the Sun, the moons in orbit around the planets, and astronomical bodies rotating at relatively constant rates, as well as causing many other rotation-related effects that we will encounter throughout this book.

Try these questions: How does tripling the linear momentum of an object change its kinetic energy? How does halving the angular momentum of an object change its kinetic energy? How much work would you do if you pushed on a desk with a force of 100 N, while it moved 20 m? How much work would you do if you pushed on a desk with a force of 500 N, and it moved 0 m? What two things can you vary to change the angular momentum of an object?

(Answers appear at the end of the book.)

A-18

The isotopes of many elements are radioactive, meaning that the elements spontaneously transform into other elements. Each radioactive isotope has a distinctive half-life, which is the time that it takes half of the initial concentration of the isotope to transform into another element. After two half-lives, a radioactive isotope is reduced to ½ × ½ or ¼ of its initial concentration (see Figure Q-1). Among the most important radioactive elements for determining the age of objects in astronomy is the isotope of uranium with 146 neutrons, ²³⁸U (“U two-thirty-eight”). The half-life of ²³⁸U decaying into lead is 4.5 billion years.

To determine the time since an object, such as a piece of space debris discovered on Earth, solidified, scientists estimate how much lead the object had when it formed. Then they measure the amounts of uranium and lead that it contains now. Subtracting the amount of original lead, they use the amount of uranium and lead, together with the graph of radioactive decay, to determine the object’s age.

Example: Suppose a piece of space debris discovered on Earth was determined to have equal amounts of lead and uranium. How long ago did this debris form? Assuming that it originally had no lead, we see from the chart that a 1-to-1 mix of lead to uranium occurs 4.5 billion years after the object formed. This period is one half-life of uranium.

Compare! This process works with any radioactive isotope. However, some isotopes have such short half-lives that they are not useful in astronomy. For example, the well-known carbon dating used to determine the ages of ancient artifacts on Earth is of little use in astronomy because ¹⁴C has a half-life of only 5730 years. Because so much of the carbon in a sample has decayed away by then, carbon dating is useful only for time intervals shorter than 100,000 years, usually a period over which little of astronomical importance occurs.

Try these questions: What fraction of a kilogram of radioactive material remains after three half-lives have passed? Using Figure Q-1, estimate how much uranium will remain after 6 billion years. Approximately how many half-lives of ¹⁴C pass in 100,000 years?

(Answers appear at the end of the book.)

From Newton’s law of gravitation, if two objects that have masses m₁ and m₂ are separated by a distance r, then the gravitational force, F, between them is

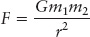
In this formula, G is the universal constant of gravitation.

The equation F = G(m₁m₂/r²) gives, for example, the force from the Sun on Earth and, equivalently, the force from Earth on the Sun. If m₁ is the mass of Earth (6.0 × 10²⁴ kg), m₂ is the mass of the Sun (2.0 × 10³⁰ kg), and r is the distance from the center of Earth to the center of the Sun (1.5 × 10¹¹ m):

F = 3.6 × 10²² N

where N is the unit of force, a newton. This number can then be used in Newton’s second law, F = ma, to find the acceleration of Earth due to the Sun. This yields

a_Earth = F/m_Earth = 6.0 × 10⁻² m/s²

Newton’s third law says that Earth exerts the same force on the Sun, so the Sun’s acceleration due to Earth’s gravitational force is

a_Sun = F/m_Sun = 1.8 × 10⁻⁸ m/s²

In other words, Earth pulls on the Sun, causing the Sun to move toward it. Because of the Sun’s greater mass, however, the amount that the Sun accelerates Earth is more than 300,000 times greater than the amount that Earth accelerates the Sun.

Try these questions: Earth’s radius is 6.4 × 10⁶ m and 1 kg is a mass equivalent to a weight of 9.8 N (or 2.2 lb) on Earth. What is the force that Earth exerts on you in newtons and pounds? What is the force that you exert on Earth in these units? What would the Sun’s force (in newtons) be on Earth if our planet were twice as far from the Sun as it is? How does that force compare to the force from the Sun at our present location? (Answers appear at the end of the book.)

A-19

A-20