Chapter 1. Electrical Events in Neurons: Resting potential
1.1 Broad overview of electrical events in neurons.
The wonderful behavioral complexity generated by the nervous system depends critically on very basic electrical and chemical events that underlie the ability of the nerve cells to communicate with each other and with the organs such as the muscles and glands that produce behavior. These events involve flows of ions such as Na and K across that cell membrane of neurons that lead to change in the electrical potential difference across the membrane. These electrical events in turn trigger release of chemicals by the neurons that affect other neurons and are the primary means of communication between neurons. In order to understand the nervous system we must have a fundamental understanding of these electrical and chemical events.
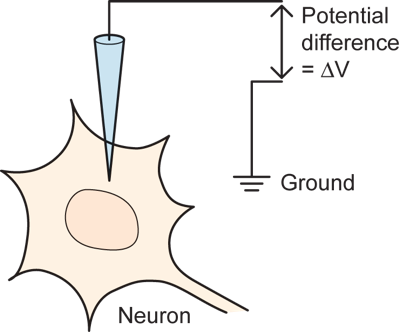
Some of the essential electrical and chemical events that underlie nervous system function can be seen in one of the most basic experiments performed by neuroscientists. The experiment involves recording the electrical potential difference across the membrane of a nerve cell in an intact animal. This is done by impaling the neuron with a glass microelectrode that is produced by heating the middle of a glass tube and pulling hard on the two ends to produce a very fine tip (typically a fraction of one micron in size) that can penetrate the cell membrane of a small neuron without destroying it. The electrode is filled with saline solution and the potential across the membrane is measured in comparison to a reference, or ground, located outside of the cell by using an amplifier. (If you are not familiar with the concepts of potential difference, current, or resistance, which are critical for understanding electrical events in neurons then go to digression on potential difference).
If you are not comfortable with potential difference, click here...
Digression: Primer on Potential Difference
Marc, somehow we will need to have a way of optimally activating digressions such as this, so the main flow need not be interrupted.
If you are not already comfortable with potential difference (voltage) and current, and in particular with Ohms law, then this Primer will give you the essential background. An understanding of Ohms law and the relationship between voltage, current, and resistance is critical for understanding electrical activity in neurons, so if you have any doubts, review it here!
Most of us are familiar with potential difference or voltage from our use of batteries. A potential difference (voltage) represents a force that has the ability to move charged particles. In batteries and wires, electrons are carrying the charge. In neurons, it is charged ions such as Na and K.
Lets review the relationships between voltage, current and resistance using a simple example.
Suppose we have a battery. They typically have two terminals, one positive and the other negative.
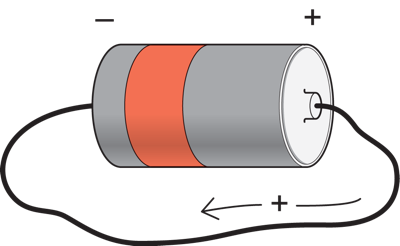
If we connect a wire from the positive to the negative terminal, a current will flow through the wire from one terminal to the other. By convention, this is considered to be a positive charge flowing from the positive terminal to the negative one (even though it is really carried by electrons flowing in the opposite direction). If we think of the battery as a force pushing charge, then the more force, or the bigger the potential difference between the battery terminals, the bigger the current that will flow. A 5 volt battery would cause more current flow through the same wire than a one volt battery. The current through the wire is affected not only by the voltage of the battery, but also by how easily the current can flow from one end of the battery to the other. If the wire has a small diameter, then it will be hard for the current to flow through it, and the current flow through the wire will be smaller than it would be through a thicker wire placed between the terminals of the same battery (just as it is easier for water to flow through a large as opposed to a small diameter tube). The opposition to current flow is called resistance. A smaller diameter wire thus has a higher resistance than a large one.
The relationship between the voltage, the current, and the resistance is described by Ohms law:
V=IR
This law involves only multiplication, so do not be thrown by its lawly status in Physics. Ohms law says that the voltage (V) is equal to the current (I) times the resistance(R).
The relationships between the three quantities is easier to understand if we re-arrange the terms:
I=V/R
Now we can see that the current flow through the wire depends on the force pushing the current (V) and the resistance of the wire. When the force (V) is higher then so is the current. Increasing the resistance, lowers the current flow through the wire. This makes sense because if there is more resistance to flow, then the flow (current) will be less.
These relationships are evident in the following simulation of Ohms law:
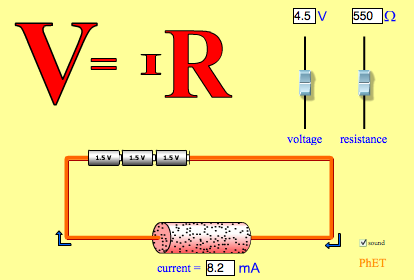
1.2 Resting Potential
Initially, before the electrode impales the neuron, when it is just sitting outside the neuron next to the ground wire, there is no potential difference and the amplifier measures zero.
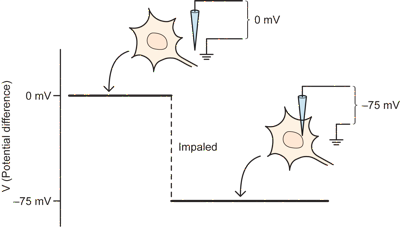
As soon as the electrode penetrates the neuron, one observes a potential difference relative to ground. The inside of the neuron is about 75 millivolts more negative than the outside. Or, in other words, the potential difference, or membrane potential is -75mV inside relative to the outside (which is treated as zero). This difference is the so-called Resting potential, and is one important feature of neurons that is critical for their ability to communicate electrically.
1.3 Synaptic Potential
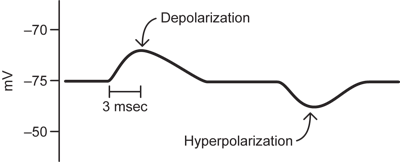
Neurons do not simply sit at resting potential. If their membrane potential is monitored over time, it will show changes. Some of these, like in the diagram below, will be relatively slow (typically milliseconds to tens of milliseconds long) changes in which the membrane potential becomes more positive or more negative for a period of time. To speak about these changes, some terminology is critical.
A depolarization occurs when the membrane potential becomes more positive (less negative) as in the first change from resting potential in the figure.
A hyperpolarization refers to the situation when the membrane potential moves in more negative than its starting potential, as in the second part of the figure.
The small long lasting depolarizations in the figure are the responses of the neuron to inputs from other neurons at the connections, or synapses, between the neurons. They are called synaptic potentials and are a prominent component of electrical recordings from neurons.
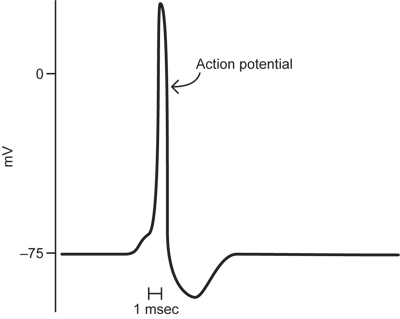
1.4 Action Potential
The last major event seen in electrical recordings from nerve cells is a very fast, very large change in potential in which the membrane potential depolarizes from a very negative resting potential to a potential that often goes above zero and then back to resting potential in as short as a millisecond. This represents a major change by about 100mV, from -75mV to above zero. This is the action potential, the electrical event that allows neurons to signal over long distances.


In order to understand how the electrical events in neurons underlie the function of neuronal circuits and the production of behavior, we need to explore how each of these events is produced. Next we consider how the resting potential is generated. Later modules will focus on synaptic potentials and action potentials.
1.5 The generation of resting potential
Neurons typically have a potential difference across their cell membranes with the inside of the neuron about -75 mV negative relative to the outside. This difference underlies many of the electrical events that neurons use to communicate with one another, so it is important to understand the origin of the resting potential. In order to understand it, we need to develop an intuition for how particles, especially charged particles, behave in solutions because it is charged ions such as Na and K that are responsible for the membrane potential.
Let's begin with a simple case:
1.6 Simple Diffusion
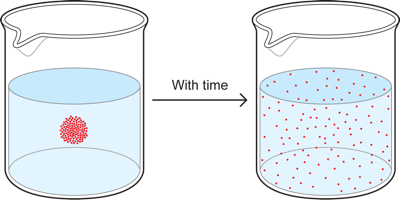
If we take a cup of water and put a drop of red dye or food coloring into the center of the cup, we will initially see a concentrated blob of red. With time, however, the red dye diffuses throughout the cup to eventually become nearly uniformly distributed in the cup, so we end up with a cup of pink water. This occurs because particles in solution tend to move, via diffusion, from where they are in high concentration to where they are in lower concentration, until the concentration is the same throughout the cup.
1.7 Two particles with semipermeable barrier
Now lets complicate the situation a bit further in two ways. First, we introduce two colors instead of one - red and blue. We also put a divider or membrane down the middle of the cup that allows only the blue particles to pass through it. What then happens?
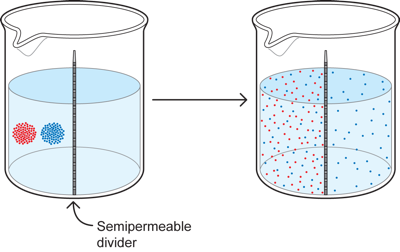
The red diffuses throughout the left side to become equal in concentration throughout that side, but it cannot get to the right, so there is none there. The blue on the other hand diffuses to become equal in concentration throughout BOTH sides because it can cross from one side to the other.
1.8 An electrical force acts along with a diffusional one
Both of these previous outcomes are the result of diffusion, a force which drives particles from where there are many to where there are few. Without ANY other force, if they are allowed to diffuse across the membrane, they will tend to distribute in equal concentrations on opposite sides of the membrane. This diffusion force that pushes particles down a concentration gradient from where there are many to where there are few is one of two major ones that contributes to the generation of resting potential.
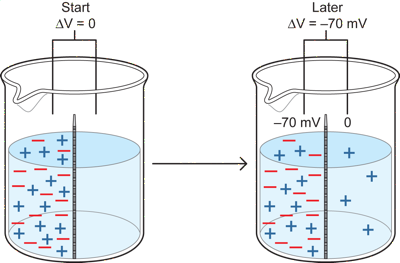
There is however another force, an electrical one. In neurons, diffusion and electrical forces both act at the same time because the individual ions, such as Na and K ions, responsible for the resting potential carry a charge and are in different concentrations inside and outside a neuron. To see how the two forces interact, lets consider another case in which the red and blue particles carry a charge. Each red particle has a negative charge and each blue particle a positive one. Otherwise the situation is the same as the previous one, with a membrane permeable only to blue.
Here really need some sort of interactive simulator like the Nernst one on the Middlebury site.
If we start with exactly equal numbers of red and blue particles on the left, then there will also be an equal number of positive and negative charges on that side and no charged particles on the other side. This means that if we measure the potential difference between the two sides of the membrane in the cup at the start, both will be at zero and there will be no potential difference because there are equal positives and negatives on the left, and none on the right. There is, however, a strong diffusional force pushing blues to the right side.
What happens over time is that some of the blue particles diffuse over to the right side. Because they are positively charged, as they move to the right, they leave behind negative charges on the left that are not balanced with positive ones (since there were equal numbers of the two at the start and some blues are now on the right). If we arbitrarily say that the right side is always at zero potential - the reference potential), then as blue particles move to the right, the left gets more and more negative relative to the right, because there is an increasing number of negative red particles unpaired with blue ones on the left (you can just as well say that if the left is the zero reference instead of the right side, then the right gets more positive relative to the left- but for the case of neurons it will be better to think of it as the left getting more negative). Both are the same really - saying I am taller than someone is the same as saying they are shorter than I am - it simply depends on the reference point, in the first case the other person and in the second case me). The key result in this situation with charged particles is that a potential difference develops over time, with the left side more negative than the right.
1.9 An electrical force acts along with a diffusional one (part II)
What is the effect of this potential difference (or electrical force) on the movement of the blue particles? We saw previously, in a situation when they were uncharged, that the blues became equal in concentration on the two sides, because the diffusion force pushed it to that outcome. In the charged case, the diffusion is still pushing blue from left to right, BUT the electrical force (potential difference between the two sides) produced by the movement of the charged blue particles is acting as well. As blues move to the right, the left side gets more and more negative. This means there is now an electrical force (potential difference or voiltage) that acts at the same time as a concentration force). The unpaired negative red particles on the left act to try to draw the positive blue particles back to the left side. This is because unlike charges attract, so excess (red) negatives on the left will act to draw (blue) positives back from the right side. Another way to look at it is that the right side is becoming more positive than the left and that as that potential difference develops it pushes positive (blue) charged particles back to the left.
So, now we have two opposing forces. A diffusion force pushing blue to the right, from high concentration to low, but in addition, as more blues move down their concentration gradient, an increasing electrical force develops pulling them back toward the left side (or pushing them from right to left). As a result, instead of blue moving to equal concentrations on the two sides, once enough blues move to the right to develop an electrical potential difference (force) that is equal (and opposite!) to the diffusion force, the blues will stop accumulating on the right even though they are not in equal concentrations on the two sides. At this point the diffusion force from the concentration difference pushing blues to the right will be exactly balanced by the electrical force which is pulling (or pushing) the blues back to the left. At this equilibrium point, for every blue that moves right due to the diffusion force, one will move left due to electrical force. As long as only one charged particle in the cup is permeable, the cup will stay in that equilibrium condition indefinitely, with a sustained potential difference across the membrane.
Important point: Very few blue particles have to move across the membrane to change the potential by many millivolts if each carries a single positive charge. Consequently, the electrical force opposing the concentration gradient builds up very fast with little blue movement. This means that even though some blues go from left to right, the concentration on the left barely changes, so the blues still are much higher on the left than right, even after the electrical and diffusion forces are in balance. While some blue particles move, not many do, so effectively the concentrations change very little from their starting levels. We end up with both an electrical potential difference across the membrane, as well as a concentration difference.
1.10 K and Cl
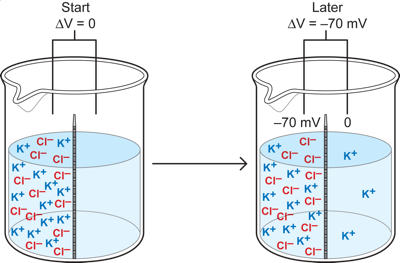
Now, one final non-neuronal case, which has the most direct parallels with what is happening in a neuron. Here we replace the reds and blues with potassium ions and Chloride ions. Imagine that we put equal amounts of K+ and Cl-, with positive and negative charges respectively, on the left side of the cup at a concentration of 100mM and we also put K+Cl- on the right side as well, but at a much lower concentration of 10mM. We assume that the membrane is permeable only to the K+. Since we start with the left side having equal numbers of K and Cl ions (100mM of each) and the right side also has equal concentrations of both (1mM each), there is initially no potential across the membrane because every K and Cl has a counterpart on each side. But, with time the K ions behave just like the blue particles in the previous example: some move to the right down the concentration gradient from the 100mM side to the 10mM one. This leads to the development of a potential difference between the two sides (as unpaired Cl- ions are left behind on the left side). The left side becomes negative relative to the right and that potential difference opposes the diffusion force by drawing (or pushing) K ions back to the left. When the electrical force becomes strong enough to oppose any further movement of K+ to the right side, then the situation becomes a stable one with a potential difference between the two sides and a sustained concentration gradient. This is an equilibrium condition, in which for every K+ ion that might move to the right, another moves to the left, so there is NO change in the concentration of the K on the two sides when the stable potential difference is reached.
1.11 Nernst Equation
Walter Nernst developed a quantitative understanding of this balance between electrical and chemical events, for which he won a Nobel prize in ???. The equation he developed is the Nernst equation. The equation is derived by considering the force of ion diffusion and asking at what potential will this force on ions be exactly opposed by the electrical force due to the potential difference. If you wish to explore the derivation of the Nernst equation you can do so here (link to derivation part), although it is not critical for rest of this module.
Nernst Equation:
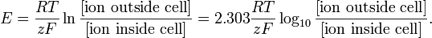
Terms in the equation:
E
R
T
Z
F
Describe the basics of why the terms matter...
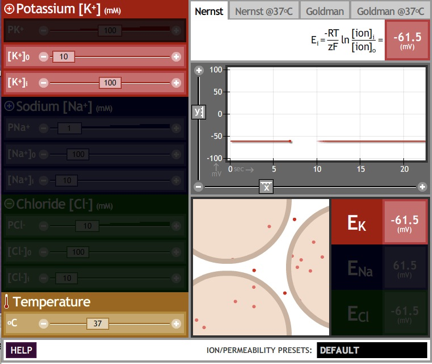
1.12 Nernst Simulator Description
Click here to zoom.
This simulator allows for simulation of both the Nernst potential at different temperatures, ion concentrations, and permeabilities, as well as the Goldman potential (to be covered later) for different temperatures, ion concentrations and permeabilities.
The left side of the program panel is where you control with a slider (or by entering a number in a slider box) the permeability of an ion and its concentration outside and inside the cell. These can be controlled for K, Na and Cl, as listed from top to bottom on the left.
The bottom most control in the left column controls the temperature.
The right column shows, in tabs at the very top, what is being simulated: either the Nernst; Nernst at 37 degrees only; Goldman; or Goldman at 37 degrees only. Clicking a tab switches among these possibilities.
Below the tab is the equation being simulated, and to the right of it, the membrane potential for whatever settings you have chosen.
Below the equation is a very useful plot showing exactly how membrane potential (inside relative to outside, with the outside being zero) changes as you vary permeabilities and concentrations on the left. This allows dynamic feedback, so as you move the sliders on the left, you can see exactly how the membrane potential shifts to get immediate feedback about how a change impacts membrane potential. You can vary the scale of the axes on the graph by dragging the x and y sliders on the axes.
Below the plot is an animation showing movements of the various color coded ions into and out of cells. To the right of this are the Nernst potentials for each of the ions for the chosen parameters.
IMPORTANT: At the very bottom right is a button labeled ion/permeability presets that allows you to return at any time to the default initial values by pressing the black button and choosing default.
1.13 Exercises and questions (I)

- Make sure that the ion/permeability presets button on the lower right is set to default.
- Set the tab on the top right to the left most one, labeled Nernst.
- The settings panel for only one of the ions is now highlighted on the left. You can click on the darkened settings for the other ions to switch the Nernst calculations from one ion to another. Try clicking on the Na or Cl settings.
- Why are the settings for only one ion visible when dealing with the Nernst calculations?
- You will notice that the permeability of the selected ion is also darkened, so you can only change the inside and outside ion concentrations and not the permeability when on the Nernst tabs of the simulator. Why is the permeability darkened? Does permeability appear in the Nernst equation? Why not? Suppose we are at the Nernst potential for an ion and suddenly increased the permeability of that ion. Would the membrane potential change? Why not?
1.14 Exercises and questions (II)

- Choose the K ion controls on the left. The Kout should be set at 10mM and the Kin at 100mM. What is the value of the membrane potential? Why is it a negative value? Do the Nernst calculation by hand and make sure the simulator is giving the right answer! Drag the Kout to higher numbers and watch what happens to the membrane potential in the plot on the right. What direction does it go as you increase external (outside) K? Why (in words not equations) does the membrane potential get more positive (less negative)?
- Set the outside concentration and the inside concentration of K both to 100mM. What is the resulting membrane potential and why (in words, not equations)?
1.15 Exercises and questions (III)

- Now set the outside concentration of K to 100mM and the inside concentration to 10mM. This is opposite of what one normally finds in a neuron. What is the Nernst potential? How does it compare to the value at 100mM in and 10mM out?
- Find the membrane potential for K with 100mM in and 10 out and then switch to Cl and measure the membrane potential with the same concentrations, 100mM in and 10mM out. Why are they so different? What are the typical neuronal Cl concentrations, and at those, what is the Nernst potential?
1.16 Exercises and questions (IV)

- Explore the effect of ion concentrations by varying them for the different ions and see how the Nernst potential changes. If you understand how the Nernst potential arises and you know the starting potential and ion concentrations, you should be able to tell intuitively whether a rise or fall in concentration on the inside or outside will lead to a more negative (hyperpolarized) or a more positive (depolarized) membrane potential. If you do not have this sense, talk to an instructor or TA so they can help you get it.
One way to understand Nernst is to think about which way the concentration gradient will move the ions. If the concentration gradient is moving positive ions out, then the inside will get more negative. The bigger the concentration difference, the more the force pushing ions out, and the more negative the Nernst potential. If an ion is negative and at a higher concentration inside, then negative ions will flow out of the cell and the inside will become more positive. The higher the concentration of ions inside relative to outside, the more force pushing the negative ions out and the more positive the inside becomes. Think this argument through for the normal differences in concentration of Cl inside and outside a neuron.
1.17 Rules for the Nernst Equation
Some rules that you should not memorize, but instead be able to picture by thinking of how charged ions flow down their concentration gradients.
- If a permeable positive ion is at higher concentration inside a cell, then the ion will flow out (from high concentration to low!) and the inside will get more negative (less positive because it is losing positive ions) relative to the outside until the electrical membrane potential is negative enough to oppose movement of more positive ions out (because inside negativity will draw positive ions back into the cell, opposing the concentration gradient driving them out). When the concentration gradient force is exactly equal and opposite to the electrical force then the cell will be at the Nernst potential.
- If a positive ion is at higher concentration outside, then the ion will tend to flow in, making the inside more positive relative to the outside until it is so positive that the electrical force exactly opposes the concentration gradient force. In this case the inside positivity repels ions from the outside to balance the concentration force pushing them into the cell.
- If a permeable NEGATIVE ion is at higher concentration inside a cell, then the ion will flow out, and the inside will get more positive (less negative charges since some have left the cell) relative to the outside until the electrical potential is positive enough to pull the negative ions back into the cell (positive ions attract negative ones) with a force exactly equal and opposite to the concentration gradient pushing negative ions out.
You can write (or think to yourself, or say it, but the people around you might think you are nuts) the last rule starting:
- If a permeable NEGATIVE ion is at higher concentration outside a cell, then….