9.6 Chi-Square Test for the Population Standard Deviation
556
OBJECTIVES By the end of this section, I will be able to …
- Perform the test for using the critical-value method.
- Perform the test for using the -value method.
- Use confidence intervals for to perform two-tailed hypothesis tests about .
1 (Chi-Square) Test for using the Critical-Value Method
In Section 8.4, we used the distribution to help us construct confidence intervals for the population variance and standard deviation. Here, in Section 9.6, we will use the distribution to perform hypothesis tests about the population standard deviation . Why might we be interested in doing so? A pharmaceutical company that wants to ensure the safety of a particular new drug would perform statistical tests to make sure that the drug's effect was consistent and did not vary widely from patient to patient. The biostatisticians employed by the company would therefore perform a hypothesis test to make sure that the population standard deviation was not too large.
Under the assumption that is true, the statistic takes the following form:
Readers may want to review the characteristics of the distribution in Section 8.4 on page 474.
For the hypothesis test about , our test statistic is called because the values of and come from the observed data. The test statistic takes a moderate value when the value of is moderate, assuming is true, and takes an extreme value when the value of is extreme, assuming is true. This leads us to the following.
The essential idea About Hypothesis testing for the Standard Deviation
When the observed value of is unusual or extreme on the assumption that is true, we should reject . Otherwise, there is insufficient evidence against , and we should not reject .
The remainder of Section 9.6 explains the details of implementing hypothesis testing for the standard deviation. The test for may be performed using the -value method or the critical-value method. We begin with the critical-value method.
Test for : Critical-Value Method
This hypothesis test is valid only if we have a random sample from a normal population.
Step 1 State the hypotheses.
Use one of the forms in Table 13. State the meaning of .
Step 2 Find the critical value or values and state the rejection rule.
Use Table 13.
Step 3 Calculate .
Either use technology to find the value of the test statistic or calculate the value of as follows:
557
which follows a distribution with degrees of freedom, and where represents the sample variance.
Step 4 State the conclusion and the interpretation.
If falls in the critical region, then reject . Otherwise do not reject . Interpret your conclusion so that a nonspecialist can understand.
The critical values in the right-tailed, left-tailed, or two-tailed tests use the following notations: , , , and (see Table 13). In each case, the subscript indicates the area to the right of the critical value. Find these values just as you did in Section 8.4, using either technology or Table E, Chi-Square () Distribution, in the Appendix.
| Right-tailed test | Left-tailed test | Two-tailed test |
|---|---|---|
|
||
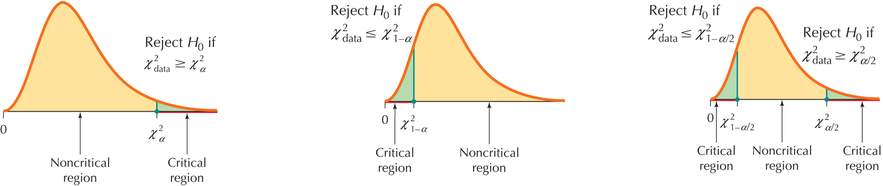
EXAMPLE 31 test for using the critical-value method
carbonemissions8
| State | Carbon emissions (millions of metric tons) |
|---|---|
| Florida | 230.98 |
| Kentucky | 148.36 |
| Missouri | 135.54 |
| New Hampshire | 16.41 |
| New Mexico | 56.60 |
| New York | 166.32 |
| Tennessee | 105.73 |
| Virginia | 99.86 |
The table contains the carbon emissions from all sources for a random sample of eight states. Test whether the population standard deviation of carbon emissions differs from 60 million metric tons, using level of significance .
558
Solution
The normal probability plot indicates acceptable normality.
Step 1 State the hypotheses.
The phrase “differs from” indicates that we have a two-tailed test. The value answers the question “Differs from what?” (Note that is 60, and not 60,000,000 because the data are expressed in millions.) Thus, we have our hypotheses:
where represents the population standard deviation of carbon emissions in millions of metric tons.
Step 2 Find the critical values and state the rejection rule.
We have , so . Because is given as 0.05, and . Then, from the table (Appendix Table E), we have , and . We will reject if is either or .
Step 3 Find .
The descriptive statistics in Figure 43 tell us that the sample variance is , squared.
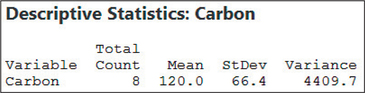Figure 9.54: FIGURE 43 Descriptive statistics from Minitab.Thus, our test statistic is:
Step 4 State the conclusion and the interpretation.
In Step 2, we said that we would reject if was either . Because is neither (see Figure 44), we do not reject . There is insufficient evidence at level of significance that the population standard deviation of the state carbon emissions differs from 60 million.
559
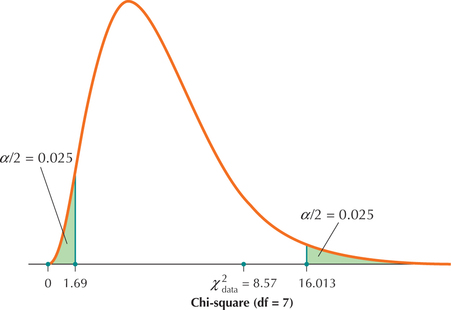Figure 9.55: FIGURE 44 does not fall in critical region, so do not reject .
NOW YOU CAN DO
Exercises 7–12.
2 Test for Using the -Value Method
We may also use the -value method to perform the test for .
test for : -value Method
This hypothesis test is valid only if we have a random sample from a normal population.
Step 1 State the hypotheses and the rejection rule.
Use one of the forms in Table 14. State the rejection rule as “Reject when the .” State the meaning of .
Step 2 Calculate .
Either use technology to find the value of the test statistic or calculate the value of as follows:
which follows a distribution with degrees of freedom, and where represents the sample variance.
Step 3 Find the -value.
Use Table 14.
Step 4 State the conclusion and the interpretation.
If the , then reject . Otherwise, do not reject . Interpret your conclusion so that a nonspecialist can understand.
| Right-tailed test | Left-tailed test | Two-tailed test |
|---|---|---|
|
If , then
If , then
|
||
|
||
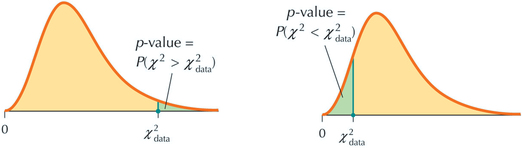
560
EXAMPLE 32 test for using the -value method and technology
The table contains the calories in ten entrée food items, courtesy of Food-A-Pedia. Test whether the population standard deviation is larger than 100 calories, using level of significance .
entreecalories
| Entrée item | Calories | Entrée item | Calories |
|---|---|---|---|
| Grilled steak | 387 | Ground beef (95% lean, medium patty) |
167 |
| Fried steak | 440 | Grilled pork chop (large) | 314 |
| Breaded fried steak | 600 | Fried pork chop (large) | 326 |
| Ground beef (75% lean, medium patty) |
234 | Meat pizza, thin crust, large | 325 |
| 1 large BBQ short rib with sauce | 148 | Fried catfish (breaded or battered) |
276 |
Solution
The normal probability plot in Figure 45 indicates acceptable normality, allowing us to proceed with the hypothesis test.
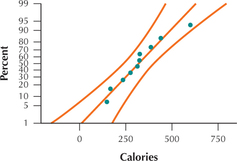
Step 1 State the hypotheses and the rejection rule.
The phrase “larger than” indicates that we have a right-tailed test. The question “Larger than what?” tells us that , giving us
We reject if the .
Step 2 Find .
We use the Step-by-Step Technology Guide on page 562. The Minitab descriptive statistics in Figure 46 tell us that the sample variance is calories squared.
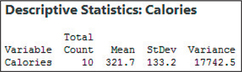Figure 9.57: FIGURE 46 Calories descriptive statistics.Thus,
Step 3 Find the -value.
For our right-tailed test, Table 14 tells us that
That is, the -value is the area to the right of , as shown in Figure 47. To find the -value, we use the instructions provided in the Step-by-Step Technology Guide provided at the end of this section. The TI-83/84 results shown in Figure 48 tell us that .
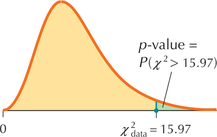Figure 9.58: FIGURE 47 -Value for test
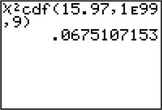Figure 9.59: FIGURE 48 TI-83/84 results.Step 4 State the conclusion and the interpretation.
Because is not , we do not reject . There is insufficient evidence that the population standard deviation is greater than 100 calories.
NOW YOU CAN DO
Exercises 13–18.
561
3 Using Confidence intervals for to Perform Two-Tailed Hypothesis Tests for
Suppose we have a confidence interval for , of the form (lower bound, upper bound), and are interested in two-tailed hypothesis tests using level of significance of the form:
We will not reject for values of that lie between the lower bound and upper bound of the confidence interval, and we will reject for values of that lie outside this interval.
EXAMPLE 33 Using confidence intervals for to conduct two-tailed tests for
A 95% confidence interval for the population mean sodium content of breakfast cereals, in milligrams (mg) per serving, is given by
Assume that the data are normally distributed. Test, using level of significance , whether differs from the following.
- 80 mg
- 40 mg
Solution
- For the hypothesis test versus lies between the lower bound 44.53 and the upper bound 81.50 of the confidence interval, and we therefore do not reject . There is insufficient evidence that the population standard deviation of sodium content differs from 80 mg.
- For the hypothesis test lies outside the confidence interval, and we therefore reject . There is evidence that the population standard deviation of sodium content differs from 40 mg.
NOW YOU CAN DO
Exercises 19–22.