Magnitude Scales
Greek astronomers, from Hipparchus in the second century b.c.e to Ptolemy (90–168 c.e.) in the second century c.e., undertook the classification of stars strictly by evaluating how bright they appear to be relative to each other. This comparison made sense because back then astronomers assumed the stars were all at the same distance from us, and, therefore, differences in brightness due to different stellar distances from Earth were not expected. Classification regardless of distance is still useful to help us navigate around the night sky, and so we will study it now. In Section 11-3 we will add the effects of different distances on how bright stars appear from Earth.
11-2 Apparent magnitude measures the brightness of stars as seen from Earth
The brightnesses of stars measured without regard to their distances from Earth are called apparent magnitudes, denoted by lowercase m. The brightest stars were originally said to be of first magnitude, and their apparent magnitudes were designated m = +1. Those stars that appeared to be about half as bright as first-magnitude stars were said to be second-magnitude stars (designated m = +2), and so forth, down to sixth-magnitude stars, the dimmest ones visible to the unaided eye. (Greek astronomers did not try to classify the Sun’s dazzling brightness in this scheme.) Because stars do not appear with discrete levels of brightness, this system has noninteger magnitudes as well, such as +3.5 or +4.8.
AN ASTRONOMER’S TOOLBOX 11-2: Details of the Magnitude Scales
The magnitude scales were created before accurate measurements of the relative brightnesses of stars could be made, and they have since been refined. Specifically, careful measurements reveal that the original first-magnitude stars were about 100 times brighter than the original sixth-magnitude stars. Therefore, in 1856 astronomer Sir Norman Pogson (1829–1891) set the brightness factor of exactly 100 to define the range of brightness between modern first- and sixth-magnitude stars. In other words, it takes 100 stars of apparent magnitude m = +6 to provide as much light as we receive from a single star of apparent magnitude m = +1.
To find out how much brighter each magnitude is from the next dimmer one, we note that there are five integer magnitudes between first and sixth magnitude. Going from m = +6 to m = +5 increases (multiplies) the brightness we see by the same factor as going from m = +5 to m = +4, and so on. Going from m = +6 to m = +1 requires multiplying the same brightness factor from one magnitude to the next 5 times. The number we must multiply 5 times to get the range of brightness of 100 is 1001/5 ≈ 2.512, or, put another way, 2.512 × 2.512 × 2.512 × 2.512 × 2.512 ≈ 100. This mathematical statement means that each successively brighter magnitude is approximately 2.512 times brighter than the preceding magnitude.
Example: An m = +3 star is approximately 2.512 times brighter than an m = +4 star. Equivalently, it takes 2.512 fourth-magnitude stars to provide as much light as we receive from a single third-magnitude star.
Try these questions after reading Section 11-2: How much brighter is an m = 0 star than an m = +4 star? How much brighter is an m = –2 star than an m = +5 star? If one star is 7.93 times brighter than another and the brighter star has an absolute magnitude of m = +3, what is the absolute magnitude of the dimmer star? (Hint for last question: Recall that magnitudes need not be integers.)
(Answers appear at the end of the book.)
More quantitative methods of classifying stars were developed in the mid-nineteenth century (see An Astronomer’s Toolbox 11-2: Details of the Magnitude Scales). While maintaining the basic idea that the apparent magnitudes of brighter objects are smaller numbers than the apparent magnitudes of dimmer ones, the scale used today begins by giving the star Vega an apparent magnitude of 0.0. Because some bodies are brighter than Vega, astronomers assign negative numbers to the apparent magnitudes of the very brightest objects. Sirius, the brightest star in the night sky, has an apparent magnitude of m = −1.44. Figure 11-2a shows Sirius along with the apparent magnitudes of some of the stars in Orion. With this convention we can describe other bright objects in the sky, such as the Sun, the Moon, comets, and planets. At its brightest, Venus shines with an apparent magnitude of m = −4.4, the full Moon has an apparent magnitude of m = −12.6, and the Sun has an apparent magnitude of m = −26.7. Remember: Objects with negative apparent magnitudes appear brighter than those with positive apparent magnitudes—the more negative, the brighter.
346
Astronomers also extended the magnitude scale so that dimmer stars, visible only through telescopes, could be included in the magnitude system. For example, the dimmest stars visible through a pair of powerful binoculars have an apparent magnitude of about m = +10. Time-exposure photographs through telescopes reveal even dimmer stars. The Keck telescopes and the Hubble Space Telescope, among others, image stars as dim as magnitude m = +30. Figure 11-2b illustrates the modern apparent magnitude scale. Similarly, apparent magnitudes from entire groups of stars, such as distant galaxies, can be measured.
Insight Into Science: Bigger Is Not Necessarily Brighter
Numbering as well as naming schemes may be counterintuitive in science. You might expect brighter stars to have larger, more positive numbers than dimmer stars, but the apparent magnitude scheme is just the opposite. Similarly, we will see shortly that on the standard plot of stars used by astronomers, the Hertzsprung-Russell diagram, the hottest stars fall on the left and the coolest stars on the right.
347
Knowing, as we now do, that stars are at different distances from us, the apparent magnitudes do not directly reveal fundamental stellar properties. All other things being equal, the closer of two identical stars appears brighter to us (has a smaller apparent magnitude) than the farther star. We take the different distances into account with either of two measures: absolute magnitude and luminosity.
11-3 Absolute magnitudes and luminosities do not depend on distance
To determine the total energy emitted by each star in space, astronomers need to take into account that different stars are at different distances from Earth. They do this by calculating the brightness each star would have if they were all at the same distance from here. Knowing how far away a star really is and how bright it appears (its apparent magnitude), we can calculate how bright it would be at any distance. Absolute magnitude, M, is the brightness each star would have at a distance of 10 pc. Unfortunately, absolute magnitudes have the same counterintuitive numeric scale as apparent magnitudes.
Margin Question 11-2
Question
What might cause the closer of two identical stars to appear dimmer than the farther one?
To understand the relationship between the apparent magnitude and the absolute magnitude, we need to know how the brightness of an object changes with distance. Suppose we observe two identical stars, one twice as far away as the other. How much dimmer will the farther one appear to be, as seen from Earth? Light moving outward from a source spreads over increasingly larger areas of space, and therefore its brightness decreases with increasing distance. The inverse-square law provides the rule for just how quickly the brightness of an object changes with distance.
Imagine light moving out from a star (Figure 11-3a). Start with a small square area of light that has moved out a distance d = 1. The light in that square has a certain brightness. When the same square of light has gone twice as far (d = 2), you can see on the figure that it has become 4 times larger. The light in each of the same-sized squares at d = 2 contains one-quarter of the photons that were in the single square at d = 1. Therefore, each small square at d = 2 is one-quarter as bright as the same-sized square at d = 1. Similarly, when the square of light has moved to d = 3, there are now nine squares the same size as the original, each one-ninth as bright as the original square at d = 1. For example, the Sun emits 3.83 × 1026 W (watts) of power (compared to 100 W for a bright home light-bulb). The Sun’s power is spread over a wider area as it travels through space. When it passes Mercury, sunlight provides 9140 watts per square meter (W/m2) of space. That same energy has spread out so much that by the time it passes us at 1 AU from the Sun, it provides only 1370 W/m2. You see the same effect every day when you look at a car’s headlights at different distances (Figure 11-3b).
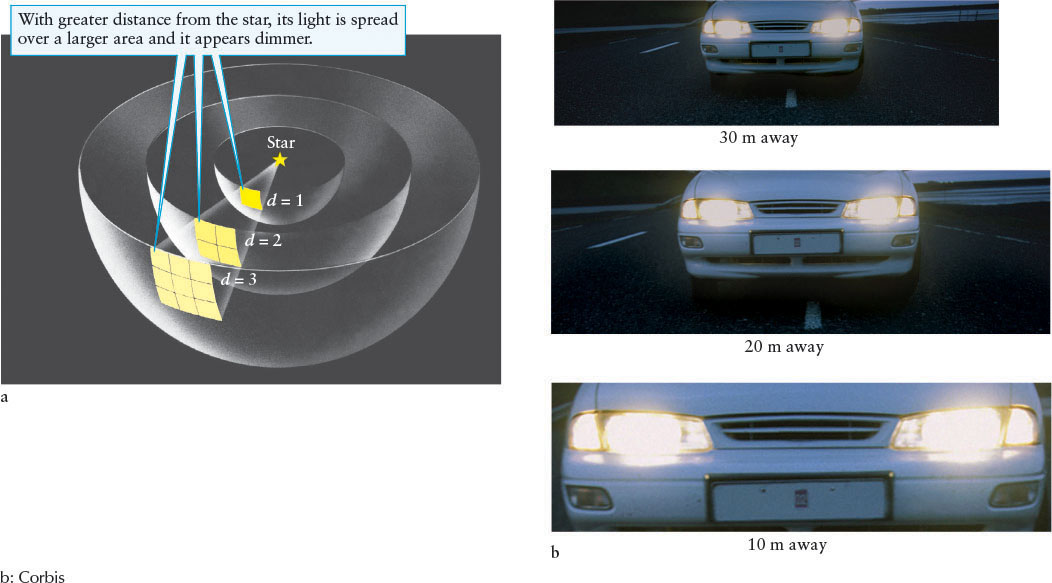
The Inverse-Square Law (a) The same amount of radiation from a light source must illuminate an ever-increasing area as the distance from the light source increases. The decrease in brightness follows the inverse-square law, which means, for example, that tripling the distance decreases the brightness by a factor of 9. (b) The car is seen at distances of 10 m, 20 m, and 30 m, showing the effect described in part (a).
348
GUIDED DISCOVERY: Star Names
Many prominent stars received names from early Arabic or Greek stargazers. For example, Aldebaran is from the Arabic for “the follower” because it follows the prominent star cluster Pleiades around the sky. Betelgeuse, located in the shoulder of the constellation Orion, takes its name from the Arabic for “armpit of the central one.” The name Sirius comes from the Greek for “sparkling,” while Arcturus is from the Greek for “bear guard,” because it is the brightest star in the constellation Boötes (the Herdsman), next to the Great Bear (Ursa Major).
Unlike Betelgeuse or Aldebaran, most stars never received fanciful names. Indeed, most are so dim that they have been observed only through telescopes in the last two centuries. To study the stars yourself, you must be able to keep track of them. Astronomers have created a system of labels for all of them.
Up to the 24 most prominent stars in each constellation are assigned Greek lowercase letters:
| α alpha | ι iota | ρ rho |
| β beta | κ kappa | σ sigma |
| γ gamma | λ lambda | τ tau |
| δ delta | μ mu | υ upsilon |
| ε epsilon | ν nu | φ phi |
| ζ zeta | ξ xi | χ chi |
| η eta | ο omicron | ψ psi |
| θ theta | π pi | ω omega |
A bright star’s name is a Greek letter together with the Latin possessive (technically, genitive) form of the constellation name. The possessive forms of the names of the zodiac constellations are:
| Constellation | Possessive |
|---|---|
| Aries | Arietis |
| Taurus | Tauri |
| Gemini | Geminorum |
| Cancer | Cancri |
| Leo | Leonis |
| Virgo | Virginis |
| Libra | Librae |
| Scorpius | Scorpii |
| Ophiuchus | Ophiuchi |
| Sagittarius | Sagittarii |
| Capricornus | Capricorni |
| Aquarius | Aquarii |
| Pisces | Piscium |
In most cases, the brightest star in the constellation is α, the second brightest is β, the third is γ, and so on. For example, the brightest star in the constellation Leo is called α Leonis. This name is more informative than its common name, Regulus.
For the millions of stars extending beyond the 24 brightest in each constellation, a variety of catalogs list the stars numerically. For example, HDE 226868 is a bright blue star, the 226,868th star in the Henry Draper Extended Catalogue of stars.
Caveat emptor: The naming of stars is the responsibility of the International Astronomical Union, which does not ever recognize the commercial sale of star names. Companies that offer to name a star for a price do not have any official standing or recognition in the astronomical community, and neither do the names they promulgate. You can pay them to name a star for you, but the name is absolutely not official.
This inverse-square law can be summarized mathematically as follows:
Apparent brightness decreases inversely with the square of the distance between the source and the observer.
Returning to our two identical stars, one twice as far away as the other, the farther one’s brightness decreases to (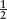
)2, or 
of the brightness, of its closer twin by the time the starlight gets to us.
Absolute magnitudes are usually determined by calculations based on apparent magnitudes. Of course, we cannot just move a star to 10 pc distance and then remeasure its apparent magnitude. However, we can calculate the absolute magnitude of a nearby star: We first measure its apparent magnitude and then we find its distance by measuring its parallax angle. Combining these numbers, as shown in An Astronomer’s Toolbox 11-3: The Distance-Magnitude Relationship, gives the star’s absolute magnitude.
349
AN ASTRONOMER’S TOOLBOX 11-3: The Distance-Magnitude Relationship
The closer a star, the brighter it appears. The inverse-square law leads to a simple equation for absolute magnitude, M. Suppose a star’s apparent magnitude (corrected for dimming due to interstellar gas and dust) is m and its distance from Earth is d (measured in parsecs). Then
M = m − 5 log (d/10)
where log stands for the base-10 logarithm. This distance-magnitude relation can be rewritten as
m − M = 5 log d − 5
Example: Consider Proxima Centauri, the nearest star to Earth (other than the Sun). By measuring its parallax angle, we know this star is at a distance from Earth of d = 1.3 pc. Its apparent magnitude is m = +11.1. Therefore, its absolute magnitude is
M = 11.1 − 5 log (1.3/10) = 11.1 − (−4.4) = +15.5
Compare! The Sun is an average star with M = +4.8, so Proxima Centauri is an intrinsically dim star. If you know any two of d, m, and M, you can calculate the third variable. For example, if we know a star’s absolute and apparent magnitudes, the equation can be used to determine its distance.
Try these questions: A star is observed to have an apparent magnitude m = +0.268 and an absolute magnitude M = −0.01. How far from Earth is the star in parsecs and light-years? A star is observed to have an apparent magnitude m = +1.17 and is at a distance of 25.1 ly from Earth. What is its absolute magnitude? (Remember to convert to parsecs first.) A star is at a distance from Earth of 8.61 ly and has an absolute magnitude of m = +1.45. What is its apparent magnitude? You can check your results and identify the stars by referring to Appendix Table E-5 and Table E-6.
(Answers appear at the end of the book.)
Knowing the Sun’s true distance and its apparent magnitude, we can use the inverse-square law to determine how bright it would appear at 10 pc. At that distance, it would have an apparent magnitude of m = +4.8. Therefore, the absolute magnitude of the Sun is M = +4.8.
Because absolute magnitudes tell astronomers how bright stars are compared with one another, this information can be used to evaluate models of stellar evolution, which we discuss in the next few chapters. Absolute magnitudes range from roughly M = −10 for the brightest stars to M = +17 for the dimmest. Although absolute magnitudes give us comparisons between the energy outputs of stars, we also need to know the total energy they release. The total amount of electromagnetic power (energy emitted each second) is called a star’s luminosity. We saw in Chapter 4 that the greater the luminosity, the intrinsically brighter the star is compared to stars with lower luminosities. Therefore, the smaller or more negative a star’s absolute magnitude, the greater its luminosity. For convenience, stellar luminosities are expressed in multiples of the Sun’s luminosity, denoted L⊙. As we saw earlier, this value is about 3.83 × 1026 W. The intrinsically brightest stars (M = −10) have luminosities of 106 L⊙ In other words, each of these stars has the energy output of a million Suns. The dimmest stars (M = +17) have luminosities of 10−5 L⊙. We will provide both luminosity and absolute magnitude data about stars in the chapters that follow.