Kepler’s and Newton’s Laws
Until Kepler’s time, astronomers had assumed that heavenly objects move in circles. For philosophical and aesthetic reasons, circles were considered the most perfect and most harmonious of all geometric shapes. However, using circular orbits failed to yield accurate predictions for the positions of the planets. For years, Kepler tried to find a shape for orbits that would fit Tycho’s observations of the planets’ positions against the background of distant stars. Finally, he began working with a geometric form called an ellipse.
53
2-5 Kepler’s laws describe orbital shapes, changing speeds, and the lengths of planetary years
You can draw an ellipse as shown in Figure 2-8a. Each thumbtack is at a focus (plural foci). The longest diameter (major axis) across an ellipse passes through both foci. Half of that distance is called the semimajor axis. In astronomy, the length of the semimajor axis is also the average distance between a planet and the Sun.
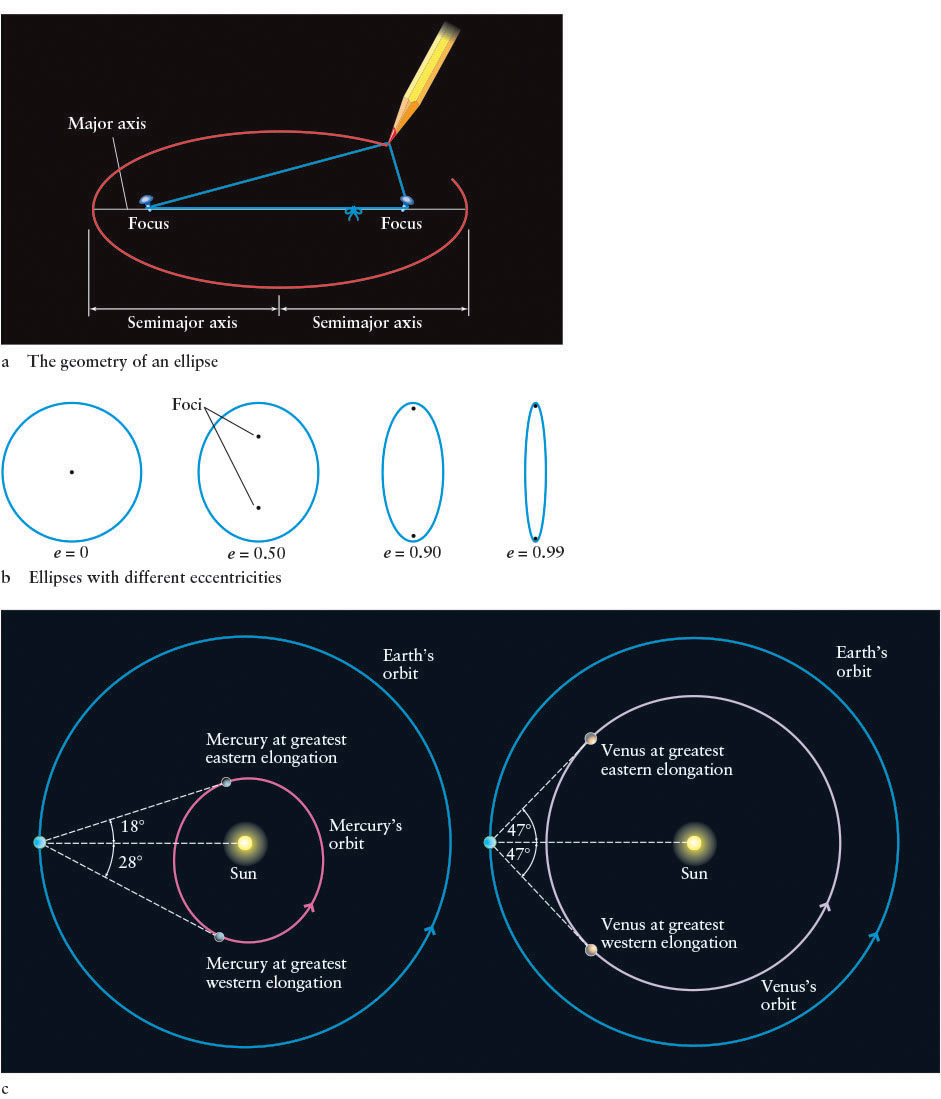
 To Kepler’s delight, the ellipse turned out to be the curve for which he had been searching. Predictions of the locations of planets based on elliptical paths were in very close agreement with where the planets actually were. Keep in mind that the following three laws that Kepler discovered merely quantified (gave equations for) observations that Tycho had made—Kepler did not have a theory to explain them. That would come nearly 80 years later, with the work of Isaac Newton.
To Kepler’s delight, the ellipse turned out to be the curve for which he had been searching. Predictions of the locations of planets based on elliptical paths were in very close agreement with where the planets actually were. Keep in mind that the following three laws that Kepler discovered merely quantified (gave equations for) observations that Tycho had made—Kepler did not have a theory to explain them. That would come nearly 80 years later, with the work of Isaac Newton.
54
Kepler published his discovery of elliptical orbits in 1609 in a book known today as New Astronomy. This important discovery is now considered the first of Kepler’s laws:
Kepler’s First Law: The orbit of each planet around the Sun is an ellipse with the Sun at one focus.
The shapes of ellipses have two extremes. The roundest ellipse, occurring when the two foci merge, is a circle. The most elongated ellipse is nearly a straight line. The shape of a planet’s orbit around the Sun is described by its orbital eccentricity, designated by the letter e, which ranges from 0 (a circular orbit) to just under 1.0 (nearly a straight line). Figure 2-8b shows a sequence of ellipses and their associated eccentricities. Observations have revealed that there is no object at the second focus of each elliptical planetary orbit. Figure 2-8c shows the effect of orbital eccentricity. For example, the maximum elongation of Mercury (e = 0.21) seen from Earth varies by 10°, while the maximum elongation of Venus (e = 0.01) varies by less than 1°.
 Tycho’s observations also showed Kepler that planets do not move at uniform speeds along their orbits. Rather, a planet moves fastest when it is nearest the Sun, a point on its orbit called perihelion. Conversely, a planet moves most slowly when it is farthest from the Sun, called its aphelion.
Tycho’s observations also showed Kepler that planets do not move at uniform speeds along their orbits. Rather, a planet moves fastest when it is nearest the Sun, a point on its orbit called perihelion. Conversely, a planet moves most slowly when it is farthest from the Sun, called its aphelion.
After much trial and error, Kepler discovered a way to describe how fast a planet moves anywhere along its orbit. This discovery, also published in New Astronomy, is illustrated in Figure 2-9. Suppose that it takes 30 days for a planet to go from point A to point B. During that time, the line joining the Sun and the planet sweeps out a nearly triangular area (shaded in Figure 2-9). Kepler discovered that the line joining the Sun and the planet sweeps out the same area during any other 30-day interval. In other words, if the planet also takes 30 days to go from point C to point D, then the two shaded segments in Figure 2-9 are equal in area. Kepler’s second law, also called the law of equal areas, can be stated thus:
Kepler’s Second Law: A line joining a planet and the Sun sweeps out equal areas in equal intervals of time.
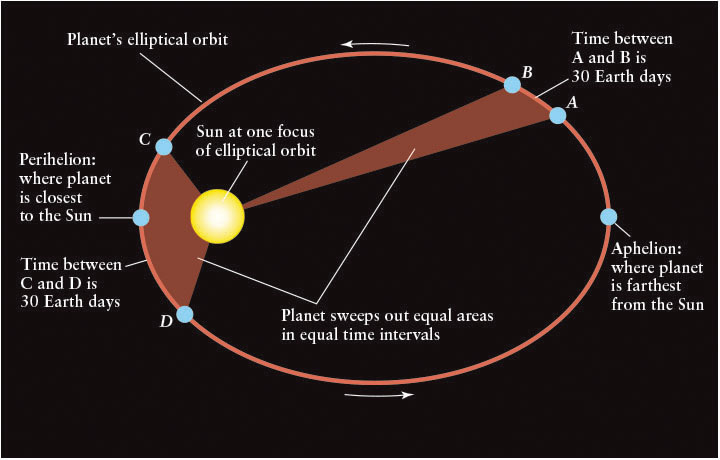
 Kepler’s First and Second Laws According to Kepler’s first law, every planet travels around the Sun along an elliptical orbit with the Sun at one focus. According to his second law, the line joining the planet and the Sun sweeps out equal areas (the burgundy-colored regions) in equal intervals of time (time from A to B equals time from C to D).
Kepler’s First and Second Laws According to Kepler’s first law, every planet travels around the Sun along an elliptical orbit with the Sun at one focus. According to his second law, the line joining the planet and the Sun sweeps out equal areas (the burgundy-colored regions) in equal intervals of time (time from A to B equals time from C to D).
A consequence of Kepler’s second law is that each planet’s speed decreases as it moves from perihelion to aphelion. The speed then increases as the planet moves from aphelion toward perihelion. Kepler was also able to relate a planet’s year to its distance from the Sun. This discovery, published in 1619, is Kepler’s third law. This relationship predicts the planet’s sidereal period if we know the length of the semimajor axis of the planet’s orbit:
Kepler’s Third Law: The square of a planet’s sidereal period around the Sun is directly proportional to the cube of the length of its orbit’s semimajor axis.

The relationship is easiest to use if we let P represent the sidereal period of an object’s orbit around the Sun in Earth years and a represent the length of its semimajor axis (that is, its average distance from the Sun) measured in astronomical units (AU). One astronomical unit is the average distance from Earth to the Sun, hence a = 1 for Earth. The astronomical unit is used when measuring distances between objects in the solar system, because no powers of ten are needed, as they would be if these distances were referred to in kilometers or miles. (See An Astronomer’s Toolbox 2-1: Units of Astronomical Distance for more details.) Now we can write Kepler’s third law for all objects orbiting the Sun as
55
56
P2 = a3
AN ASTRONOMER’S TOOLBOX 2-1: Units of Astronomical Distance
 Throughout this book we will find that some of our traditional units of measure become cumbersome. It is fine to use kilometers to measure the diameters of craters on the Moon or the heights of volcanoes on Mars. However, it is as awkward to use kilometers to express the large distances to planets, stars, or galaxies as it is to talk about the distance from New York City to San Francisco or Sydney to Perth in millimeters. Astronomers have therefore devised new units of measure.
Throughout this book we will find that some of our traditional units of measure become cumbersome. It is fine to use kilometers to measure the diameters of craters on the Moon or the heights of volcanoes on Mars. However, it is as awkward to use kilometers to express the large distances to planets, stars, or galaxies as it is to talk about the distance from New York City to San Francisco or Sydney to Perth in millimeters. Astronomers have therefore devised new units of measure.
When discussing distances across the solar system, astronomers use a unit of length called the astronomical unit (AU), which is the average distance between Earth and the Sun:
1 AU ≈ 1.5 × 108 km ≈ 9.3 × 107 mi
Jupiter, for example, is an average of 5.2 times farther from the Sun than is Earth. Thus, the average distance between the Sun and Jupiter can be conveniently stated as 5.2 AU. This value can be converted into kilometers or miles using the previous relationship.
When talking about distances to the stars, astronomers choose between two different units of length. One is the light-year (ly). A light-year is the distance that light travels in a year through a vacuum (that is, in the absence of air, glass, or other medium). Do keep in mind that the word year in this unit helps describe a separation between two objects rather than representing a unit of time.
1 ly ≈ 9.46 × 1012 km ≈ 63,200 AU
The spaces between the planets, stars, and galaxies are nearly ideal vacuums. One light-year is roughly equal to 6 trillion miles. Proxima Centauri, the closest star to Earth, other than the Sun, is just over 4.2 ly from us.
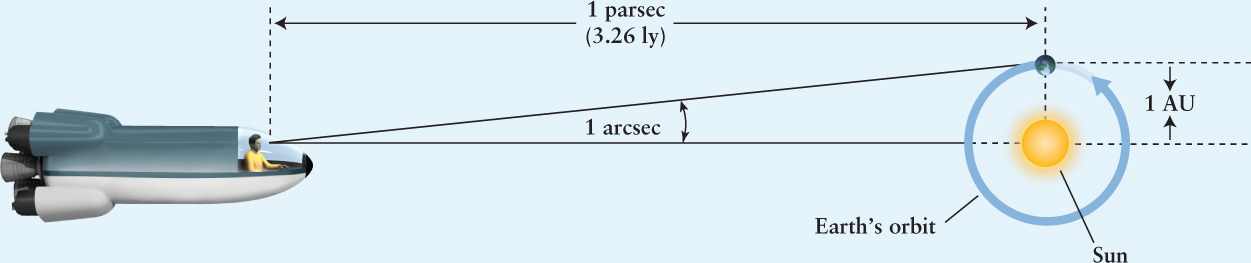
The second commonly used unit of length is the parsec (pc), the distance at which two objects separated by 1 AU make an angle of 1 arcsec. Imagine taking a journey far into space, beyond the orbits of the outer planets. Watching the solar system as you move away, the angle between the Sun and Earth becomes smaller and smaller. When they are side by side from your perspective, and you measure the angle between them as 1/3600° (called 1 arcsec; see An Astronomer’s Toolbox 1-1: Observational Measurements Using Angles for more details on angular measurements), you have reached a distance that astronomers call 1 parsec, as shown in the figure below. The parsec turns out to be longer than the light-year, specifically,
1 pc ≈ 3.09 × 1013 km ≈ 3.26 ly
Thus, the distance to the nearest star can be stated as 1.3 pc as well as 4.2 ly. Whether one uses light-years or parsecs is a matter of personal taste.
For larger distances, kilolight years (kly), megalight years (Mly), kiloparsecs (kpc), and megaparsecs (Mpc) are used. The prefixes “kilo” and “mega” simply mean “thousand” and “million,” respectively:
For example, the distance from Earth to the center of our Milky Way Galaxy is about 8.6 kpc, and the rich cluster of galaxies in the direction of the constellation Virgo is 20 Mpc away.
Try these questions: The nearest star (other than the Sun) is 4.2 ly away. How many miles away is it? How many kilometers?
(Answers appear at the end of the book.)
 This equation says that a planet closer to the Sun has a shorter year than does a planet farther from the Sun. Using this equation with Kepler’s second law reveals that planets closer to the Sun move more rapidly than those farther away. Using data from Table 2-1 and Table 2-2, we can demonstrate Kepler’s third law as shown in Table 2-3.
This equation says that a planet closer to the Sun has a shorter year than does a planet farther from the Sun. Using this equation with Kepler’s second law reveals that planets closer to the Sun move more rapidly than those farther away. Using data from Table 2-1 and Table 2-2, we can demonstrate Kepler’s third law as shown in Table 2-3.
| Sidereal period P (year) | Semimajor axis a (AU) | P2 | = | a3 | |
|---|---|---|---|---|---|
| Mercury | 0.24 | 0.39 | 0.06 | 0.06 | |
| Venus | 0.61 | 0.72 | 0.37 | 0.37 | |
| Earth | 1.00 | 1.00 | 1.00 | 1.00 | |
| Mars | 1.88 | 1.52 | 3.53 | 3.51 | |
| Jupiter | 11.86 | 5.20 | 140.7 | 140.6 | |
| Saturn | 29.46 | 9.54 | 867.9 | 868.3 | |
| Uranus | 84.01 | 19.19 | 7058 | 7067 | |
| Neptune | 164.79 | 30.06 | 27,160 | 27,160 |
When Newton derived Kepler’s third law using the law of gravitation, discussed later in this chapter, he discovered that the mass of a planet affects the period of its orbit around the Sun. The mass of an object is a measure of the total number of particles that it contains and is expressed in units of kilograms. For example, the mass of the Sun is 2 × 1030 kg, the mass of a hydrogen atom is 1.7 × 10−27 kg, and the mass of the author of this book is 83 kg. At rest, the Sun, a hydrogen atom, and I have these same masses regardless of where we happen to be in the universe. It is important not to confuse the concept of mass with the concept of weight. Your weight is the force with which you push down on a scale due to the gravitational attraction of the world on which you stand.
However, the effect of the planet’s mass on the period of its orbit is exceedingly small for all the planets in the solar system, which is why the equation for Kepler’s third law, as shown in Table 2-3, gives such good results for the planets’ orbits even though it does not take their masses into account. When calculating the motion of pairs of stars orbiting each other, the effects of the masses must be included, as described in An Astronomer’s Toolbox 11-4: Kepler’s Third Law and Stellar Masses.
Kepler’s three laws apply not only to the planets orbiting the Sun, but also to any object orbiting another under the influence of their mutual gravitational attraction. Thus, Kepler’s laws apply to moons orbiting planets, artificial satellites orbiting Earth, and even (with the above caveat) two stars revolving around each other.
WHAT IF…: Earth were fixed at the center of the universe?
Let’s return to the geocentric universe for a moment and consider a consequence of mass in the scenario where everything orbits around Earth. In 1905, Albert Einstein developed his special theory of relativity in which he showed that the faster objects move, the greater mass they acquire. If accelerated to the speed of light, 300,000 km/s (186,000 mi/s), any object that starts with even a tiny mass (such as a feather) would have more mass than everything else in the entire universe, which would make the object impossible to move. Thus, the speed of light is the ultimate speed limit. If Earth were fixed at the center of the universe and everything orbited around us, objects farther away than 1.5 × 1012 km would each have to be traveling faster than the speed of light if they were to travel around Earth once each day. Therefore, these distant stars would have infinite mass and violate the universe’s speed limit. The star closest to Earth other than the Sun is 40 × 1012 km from us. Enough said.
2-6 Galileo’s discoveries strongly supported a heliocentric cosmology
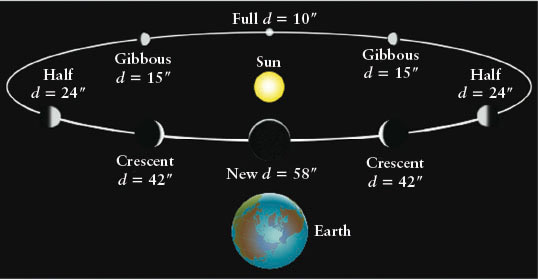
While Kepler was in central Europe working on the laws of planetary orbits, an Italian physicist was making dramatic observations in southern Europe. Galileo Galilei (1564–1642; see Guided Discovery: Astronomy’s Foundation Builders) did not invent the telescope, but he was one of the first people to point the new device toward the sky and publish his observations. He saw things that no one had ever imagined—mountains on the Moon and spots on the Sun. He also discovered that the change in the apparent size of Venus as seen through his telescope was related to the planet’s phase (Figure 2-10). Venus appears smallest at full phase and largest at new phase. These observations were a big chink in the geocentric cosmology’s armor, as that model could not explain why Venus has phases or changes size, while a heliocentric cosmology explains both. Galileo’s observations, therefore, supported the conclusion that Venus orbits the Sun, not Earth.
57
In 1610, Galileo also discovered four moons near Jupiter. Today, in honor of their discoverer, these are called the Galilean moons (or satellites, another term for moons). Galileo concluded that the moons orbit Jupiter because he saw them move in straight lines from one side of the planet to the other. (He did not see them move in elliptical orbits because from Earth we see their orbits from edge-on.) Confirming observations were made in 1620 (Figure 2-11). These observations all provided further evidence that Earth is not at the center of the universe. Like Earth in orbit around the Sun, Jupiter’s four moons obey Kepler’s third law: The square of a moon’s orbital period around Jupiter is directly proportional to the cube of its average distance from the planet.

Margin Question 2-5
Question
What is the shape of the International Space Station’s orbit around Earth?
Margin Question 2-6
Question
We saw in Chapter 1 that the Moon’s orbit around Earth is not circular. Where in its orbit is the Moon moving fastest, and where is it moving slowest?
Galileo’s telescopic observations constituted the first fundamentally new astronomical data since humans began recording what they saw in the sky. In contradiction to then-prevailing opinions, these discoveries strongly supported a heliocentric view of the universe. Because Galileo’s ideas could not be reconciled with certain passages in the Bible or with the writings of Aristotle and Plato, the Roman Catholic Church condemned him, and he was forced to spend his later years under house arrest “for vehement suspicion of heresy.” In 1992, Pope John Paul II stated that the Church erred in this condemnation.
58
Insight Into Science: Theories and Explanations
Scientific theories (or laws) based on observations can be useful for making predictions even if the reasons that these theories work are unknown. The explanation for Kepler’s laws came decades after Kepler deduced them, when Newton derived them in 1665 with his mathematical expression for gravitation, the force that holds the planets in their orbits.
A major stumbling block prevented seventeenth-century thinkers from accepting Kepler’s laws and Galileo’s conclusions about the heliocentric cosmology. Once anything on Earth is put in motion, it quickly comes to rest. So why don’t the planets orbiting the Sun stop, too?
The scientific method clarified most of the issues surrounding planetary orbits, leading to the equations and laws developed by the brilliant and eccentric (for example, he believed in alchemy) scientist Isaac Newton, who was born on Christmas Day in 1642, less than a year after Galileo died. In the decades that followed, Newton revolutionized science more profoundly than any person before him, and in doing so, he found physical and mathematical evidence in support of the heliocentric cosmology.
2-7 Newton formulated three laws that describe fundamental properties of physical reality
Until the mid-seventeenth century, virtually all mathematical astronomy was done empirically. That is, astronomers from Ptolemy to Kepler created equations directly from data and observations.
Isaac Newton (see Guided Discovery: Astronomy’s Foundation Builders) introduced a new approach. He began with three physical assumptions, now called Newton’s laws of motion, which led to equations that have since been tested and shown to be correct in many everyday situations. He also found a formula for the force of gravity (or gravitation), the attraction between all objects due to their masses. Putting the assumptions into mathematical form and combining them with the equation for gravity, Newton was able to derive Kepler’s three laws and use them to predict the orbits of bodies such as comets and other objects in the solar system. Newton also was able to use these same equations to predict the motions of bodies on and near Earth, such as the path of a projectile or the speed of a falling object.
Newton’s First Law—The Law of Inertia: Inertia is the property of matter that keeps an object at rest or moving in a straight line at a constant speed unless acted upon by a net external force.
If all of the external forces acting on an object do not cancel each other out, then there is a net external force acting on the object. Equivalently, we say that there is an unbalanced external force. For example, if you put a soccer ball between your hands and press on it so that it does not move, your hands represent a balanced pair of forces acting on the ball. In that case, you are exerting no net external force on the ball. Conversely, when your foot hits a soccer ball and the ball sails away, your foot has exerted a net external force on the ball.
At first, this law might seem to conflict with your everyday experience. For example, if you shove a chair, it does not move at a constant speed forever but comes to rest after sliding only a short distance. From Newton’s viewpoint, however, a “net external force” does indeed act on the moving chair—namely, friction between the chair’s legs and the floor. Without friction, the chair would continue in a straight path at a constant speed. A net external force changes the motion of an object.
Newton’s first law tells us why the planets keep moving in orbit around the Sun. First, they do not come to rest because there is virtually no air in space and hence no force from, for example, air friction opposing their motion. Second, they do not move in straight lines because there is an outside force acting on the planets to continually change their directions and keep them in orbit. As we shall see, that force is the Sun’s gravity.
Newton’s second law describes quantitatively how a force changes the motion of an object. To better appreciate the concepts of force and motion, we must first understand two related quantities: velocity and acceleration.
Imagine an object motionless in space. Push on it and it begins to move. At any moment, you can describe the object’s motion by specifying both its speed and direction. Speed and direction of motion together constitute an object’s velocity. If you continue to push on the object, its speed will increase—it will accelerate.
Acceleration is the rate at which velocity changes with time. Because velocity involves both speed and direction, a slowing down, a speeding up, or a change in direction are all forms of acceleration.
Suppose, for example, an object revolved around the Sun in a perfectly circular orbit. As this object moved along its orbit, its speed would remain constant, but its direction of motion would be continuously changing. This body would have acceleration that involved only a change of direction. In general:
Newton’s Second Law—The Force Law: The acceleration of an object is directly proportional to the net force acting on it and is inversely proportional to its mass.
In other words, the harder you push on something that can move, the faster it will accelerate. Also, an object of greater mass accelerates more slowly when acted on by a force than does an object of lesser mass acted on by the same force. That is why you can accelerate a child’s wagon faster than you can accelerate a car by pushing on them equally hard.
59

Newton’s second law can be succinctly stated as an equation. If a force acts on an object, the object will experience an acceleration such that
Force = mass × acceleration
 Force is usually expressed in pounds or newtons. For example, the force with which I am pressing down on the ground is 814 newtons (183 lb). But I weigh 814 newtons only on Earth. I would weigh 136 newtons (30.5 lb) on the Moon, which has less mass and so pulls me down with less gravitational force. Orbiting in the International Space Station, my weight (measured by standing on a scale in the space station) would be 0, but my mass would be the same as when I am on Earth. Because I still have inertia in the space station, I would have to push against something in order to float across the cabin. Whenever we describe the properties of planets, stars, or galaxies, we speak of their masses, never of their weights.
Force is usually expressed in pounds or newtons. For example, the force with which I am pressing down on the ground is 814 newtons (183 lb). But I weigh 814 newtons only on Earth. I would weigh 136 newtons (30.5 lb) on the Moon, which has less mass and so pulls me down with less gravitational force. Orbiting in the International Space Station, my weight (measured by standing on a scale in the space station) would be 0, but my mass would be the same as when I am on Earth. Because I still have inertia in the space station, I would have to push against something in order to float across the cabin. Whenever we describe the properties of planets, stars, or galaxies, we speak of their masses, never of their weights.
Newton’s final assumption, called Newton’s third law, is the law of action and reaction.
Newton’s Third Law—The Law of Action and Reaction: Whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first object.
Margin Question 2-7
Question
Sitting in a moving car, how can you experimentally verify that your body has inertia?
For example, I weigh 183 lb on Earth, and so I press down on the floor with a force of 183 lb. Newton’s third law says that the floor is also pushing up against me with an equal force of 183 lb. (If it were less, I would fall through the floor, and if it were more, I would be lifted upward.) In the same way, Newton realized that because the Sun is exerting a force on each planet to keep it in orbit, each planet must also be exerting an equal and opposite force on the Sun. As each planet accelerates toward the Sun, the Sun in turn accelerates toward each planet.
Margin Question 2-8
Question
How did people deduce that there is no air (and hence no air friction to slow planets down) in space before airplanes or even people-carrying balloons were invented?
Margin Question 2-9
Question
If you are on a freely spinning merry-go-round, what will happen to it as you move toward the center?
Because the Sun is pulling on the planets, why don’t they fall onto it? Conservation of angular momentum provides the answer. Angular momentum is a measure of how much energy is stored in an object due to its rotation and revolution. The details of momentum are presented in An Astronomer’s Toolbox 2-2: Energy and Momentum. As the orbiting planets fall toward the Sun, their angular momentum provides them with motion perpendicular to that infall, meaning that the planets continually fall toward the Sun, but they continually miss it. Because their angular momentum is conserved, planets neither spiral into the Sun nor fly away from it. Angular momentum remains constant unless acted on by an external torque (also defined in An Astronomer’s Toolbox 2-2).
Angular momentum depends on three things: how fast an object rotates or revolves, how much mass it has, and how spread out that mass is. Consider, for example, a twirling ice skater. She rotates with a constant mass, practically free of outside forces. Because her angular momentum is therefore conserved, she can change how fast she is spinning by changing how spread out her mass is. When she wishes to rotate more rapidly, she decreases the spread of her mass distribution by pulling her arms and outstretched leg in closer to her body (Figure 2-12). According to conservation of angular momentum, as the spread of mass decreases, the rotation rate must increase. In astronomy, we encounter many instances of the same law, as giant objects, such as stars, contract.

60
AN ASTRONOMER’S TOOLBOX 2-2: Energy and Momentum
Scientists identify two types of energy that are available to any object. The first, called kinetic energy, is associated with the object’s motion. For speeds much less than the speed of light, we can write the amount of kinetic energy, KE, of an object as
KE = ½ mv2
where m is the object’s mass and v is its speed. Kinetic energy is a measure of how much work the object can do on the outside world or, equivalently, how much work the outside world has done to give the object this speed.
Work is also a rigorously defined concept that often is at odds with our intuition. Work is defined as the product of the force, F, acting on an object and the distance, d, over which the object moves in the direction of the force:
W = Fd
For example, if I exert a horizontal force of 50 N (N is the unit newtons and is the metric unit of force) and thereby move an object 10 m in the direction I push it, then I have done 50 N × 10 m = 500 J of work. (I have used the relationship that 1 newton × 1 meter = 1 joule.)
The second type of energy is called potential energy, the energy available to an object as a result of its location in space. For example, if you hold a pencil above the ground, the pencil has potential energy that can be converted into kinetic energy by Earth’s gravitational force. How does that conversion get underway? Just let go of the pencil.
There are various kinds of potential energy, such as the potential energy stored in a battery and the potential energy stored in objects under the influence of gravity. We will focus on gravitational potential energy. Far from extremely massive objects, like stars, or extremely dense objects, like black holes, gravitational potential energy, PE, can be written as
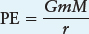
where the constant G = 6.6683 × 10−11 N m2/kg2, m is the mass of the object whose gravitational potential energy you are measuring, M is the mass of the object generating the gravitational attraction, and r is the distance between the centers of mass of these two objects.
Near the surface of Earth, this equation simplifies to
PE = mgh
where g = 9.8 m/s2 (32 ft/s2) is the gravitational acceleration at Earth’s surface, and h is the height of the object above Earth’s surface.
Potential energy can be converted into kinetic energy and vice versa. After you drop a pencil, its gravitational potential energy begins to decrease while its kinetic energy begins to increase at the same rate. The pencil’s total energy is conserved. Conversely, if you throw a pencil up in the air, the kinetic energy you give it will immediately begin to decrease, while its potential energy increases at the same rate.
Related to the motion of an object, and hence to its kinetic energy, are the concepts of linear momentum, usually just called momentum, and angular momentum. Momentum, p, is described by the equation
p = mv
where v is the velocity of the object. Both p and v are in boldface to indicate that they both represent motion in some direction or another (both in the same direction), as well as a numeric value. Simple algebra reveals that kinetic energy and momentum are related by
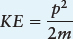
Linear momentum, then, indicates how much energy is available to an object because of its motion in a straight line (linear motion).
Angular momentum, L, can be expressed mathematically as
L = Iω
where I is the moment of inertia of an object, and ω (lowercase Greek omega) is the angular speed and direction of the rotating object. Just as an object’s mass indicates how hard it is to change an object’s straight-line motion, the moment of inertia indicates how hard it is to change the rate at which an object rotates or revolves. The moment of inertia depends on an object’s mass and shape. Kinetic energy due to angular motion can be written as
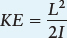
Newton’s first law can also be expressed in terms of conservation of linear momentum:
A body maintains its linear momentum unless acted upon by a net external force.
Equivalently, for angular motion we can write the conservation of angular momentum:
A body maintains its angular momentum unless acted upon by a net external torque.
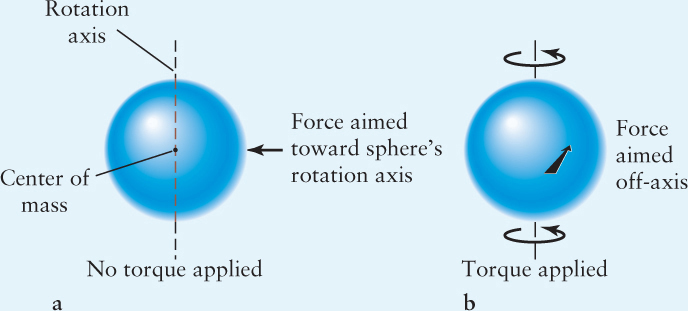
Torques are created when a force acts on an object in some direction other than toward the center of the object’s angular motion, as shown in the figure to the right.
Earth has angular momentum from two sources, namely, from spinning on its rotational axis and from orbiting the Sun. Likewise, the Moon has angular momentum because it spins on its rotation axis and it orbits Earth. Virtually all objects in astronomy have angular momentum, and it is probably fair to say that conservation of angular momentum is among the most important laws in the cosmos. After all, conservation of angular momentum is what keeps the planets in orbit around the Sun, the moons in orbit around the planets, and astronomical bodies rotating at relatively constant rates, as well as causing many other rotation-related effects that we will encounter throughout this book.
Try these questions: How does tripling the linear momentum of an object change its kinetic energy? How does halving the angular momentum of an object change its kinetic energy? How much work would you do if you pushed on a desk with a force of 100 N, while it moved 20 m? How much work would you do if you pushed on a desk with a force of 500 N, and it moved 0 m? What two things can you vary to change the angular momentum of an object?
(Answers appear at the end of the book.)
We have now reconstructed the central relationships between matter and motion. Scientific explanation of the heliocentric cosmology still requires a force to hold the planets in orbit around the Sun and the moons in orbit around the planets. Newton identified that, too.
2-8 Newton’s description of gravity accounts for Kepler’s laws
Isaac Newton did not invent the idea of gravity. An observant seventeenth-century person would understand that some force pulls things down to the ground. It was Newton, however, who gave us a quantitative description of the action of gravity, or gravitation, as it is more properly called. Using his first two laws, Newton showed mathematically that the force acting on each of the planets is directed toward the Sun. He expanded this result to the idea that the nature of the force pulling a falling apple straight down to the ground is the same as the nature of the force on the planets from the Sun. More generally, the gravitational force from every object acts to pull every other object directly toward it.
61
Newton succeeded in formulating a mathematical model that describes the behavior of the gravitational force that keeps the planets in their orbits (presented in An Astronomer’s Toolbox 2-3: Gravitational Force).
Newton’s Law of Universal Gravitation: Two objects attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
In other words, gravitational force decreases with distance. Move twice as far away from an object and you feel only one-quarter of the force from it that you felt before. Despite its weakening, the force of gravity from each object extends throughout the universe. Also, an object with twice the mass of another object exerts twice the gravitational force as the less massive object.
Using his law of gravity along with his three laws stated earlier, Newton found that he could mathematically explain Kepler’s three laws. For example, whereas Kepler discovered by trial and error that the period of orbit, P, and average distance between the Sun and planet, a, are related by P2 = a3, Newton mathematically derived this equation (corrected by including a tiny contribution due to the mass of the planet, as mentioned earlier). Bodies in elliptical orbits are bound by the force of gravity to remain in orbit.
62
AN ASTRONOMER’S TOOLBOX 2-3: Gravitational Force
From Newton’s law of gravitation, if two objects that have masses m1 and m2 are separated by a distance r, then the gravitational force, F, between them is
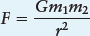
In this formula, G is the universal constant of gravitation, introduced in An Astronomer’s Toolbox 2-2.
The equation F = G (m1m2/r2) gives, for example, the force from the Sun on Earth and, equivalently, the force from Earth on the Sun. If m1 is the mass of Earth (6.0 × 1024 kg), m2 is the mass of the Sun (2.0 × 1030 kg), and r is the distance from the center of Earth to the center of the Sun (1.5 × 1011 m):
F = 3.6 × 1022 N
where N is the unit of force, a newton. This number can then be used in Newton’s second law, F = ma, to find the acceleration of Earth due to the Sun. This yields
aEarth = F/mEarth = 6.0 × 10−2 m/s2
Newton’s third law says that Earth exerts the same force on the Sun, so the Sun’s acceleration due to Earth’s gravitational force is
asum = F/msum = 1.8 × 10−8 m/s2
In other words, Earth pulls on the Sun, causing the Sun to move toward it. Because of the Sun’s greater mass, however, the amount that the Sun accelerates Earth is more than 300,000 times greater than the amount that Earth accelerates the Sun.
Try these questions: Earth’s radius is 6.4 × 106 m and 1 kg is a mass equivalent to a weight of 9.8 N (or 2.2 lb) on Earth. What is the force that Earth exerts on you in newtons and pounds? What is the force that you exert on Earth in these units? What would the Sun’s force be on Earth if our planet were twice as far from the Sun as it is? How does that force compare to the force from the Sun at our present location?
(Answers appear at the end of the book.)
 It seems plausible that astronauts floating in the International Space Station do not feel any force of gravity from Earth, but they do. Orbiting 330 km (approximately 200 mi) above Earth’s surface, they feel 90% as much gravitational force from the planet as we do standing on it. They are weightless, however, because as they fall earthward, their angular momentum carries them around the planet at just the right rate to continually miss it.
It seems plausible that astronauts floating in the International Space Station do not feel any force of gravity from Earth, but they do. Orbiting 330 km (approximately 200 mi) above Earth’s surface, they feel 90% as much gravitational force from the planet as we do standing on it. They are weightless, however, because as they fall earthward, their angular momentum carries them around the planet at just the right rate to continually miss it.
Newton also discovered that some objects orbiting the Sun can follow nonelliptical paths. His equations led him to conclude that orbits can also be parabolas or hyperbolas (Figure 2-13). In both cases, such bodies would make only one pass close to the Sun and then travel out of the solar system, never to return. To date, all of the objects observed in the solar system began their existence in elliptical orbits, but some comets (small bodies of rock and ice) have received enough energy from being pulled by planets or from expelling jets of gas to develop parabolic or hyperbolic orbits.
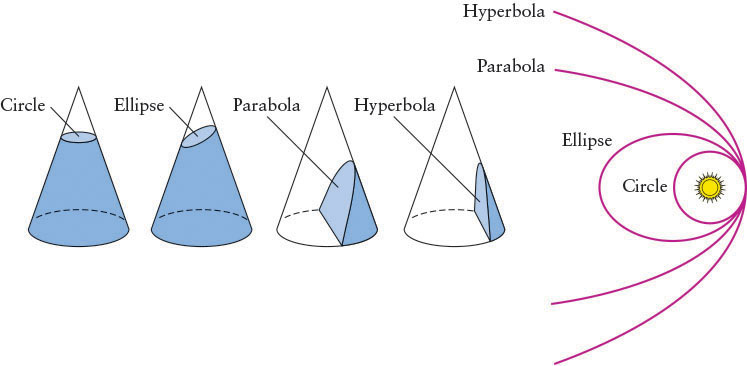
63
Using the equations Newton derived, the orbits of the planets and their satellites could be calculated with unprecedented precision. Using his laws, mathematicians showed that Earth’s axis of rotation must precess because of the gravitational pull of the Moon and the Sun on Earth’s equatorial bulge (recall Figure 1-21). In the spirit of the scientific method, Newton’s laws and mathematical techniques were used to predict new phenomena. For example, Edmond Halley was intrigued by historical records of a comet that was sighted about every 76 years. Using his friend Newton’s methods, Halley worked out the details of the comet’s orbit and predicted its return in 1758. It was first sighted on Christmas night of that year, and to this day the comet bears Halley’s name (Figure 2-14).

WHAT IF…: The International Space Station Didn’t Feel Any Gravity from Earth?
Newton’s first law says that the space station will move in a straight line unless acted upon by a net external force. Without gravity, there would be no external force acting on the station, so it, and everything in it, would move together in a straight line—instead of orbiting Earth, the space station would move away from us.
Perhaps the most dramatic early use of the scientific method with Newton’s ideas was their role in the discovery of the eighth planet in our solar system. The seventh planet, Uranus, had been discovered by William Herschel (1738–1822) in 1781 during a systematic telescopic survey of the sky. Fifty years later, however, it was clear that Uranus was not following the orbit predicted by Newton’s laws. Two mathematicians, John Couch Adams (1819–1892) in England and Urbain-Jean-Joseph Leverrier (1811–1877) in France, independently calculated that the deviations of Uranus from its predicted orbit could be explained by the gravitational pull of a then unknown, more distant planet. Each man predicted that the planet would be found at a certain location in the constellation of Aquarius in September 1846. A telescopic search on September 23, 1846, by German astronomer Johann Galle (1812–1910), revealed Neptune less than 1° from its calculated position. Although sighted with a telescope, Neptune was really discovered with pencil and paper.
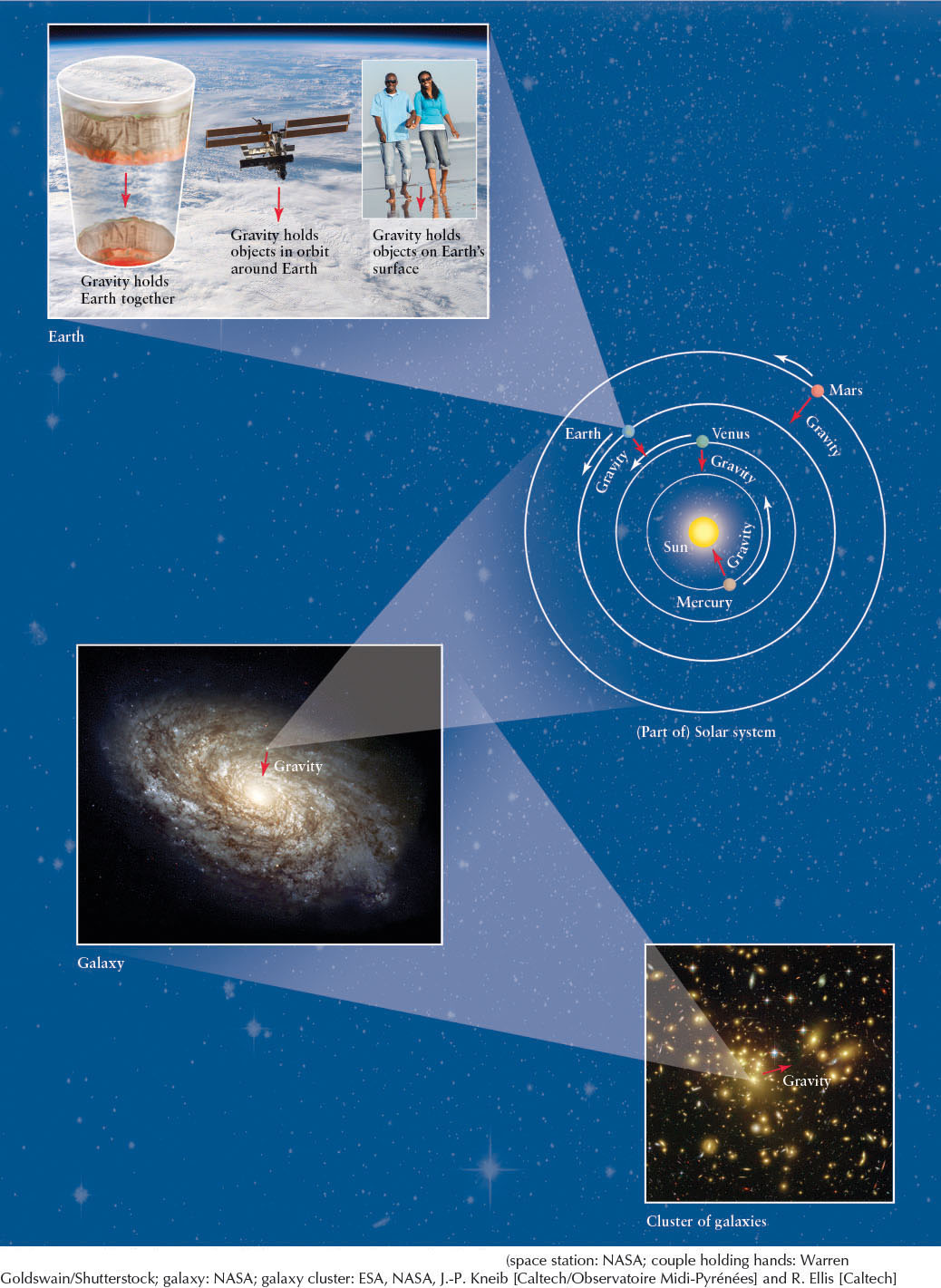
 It is a testament to Newton’s genius that his three laws were precisely the basic ideas needed to understand so much about the natural world. Newton’s process of deriving Kepler’s laws and the universal law of gravitation helped secure the scientific method as an invaluable tool in our process of understanding the universe. Figure 2-15 shows some of the effects of gravity at the scales of planets, stars, and galaxies.
It is a testament to Newton’s genius that his three laws were precisely the basic ideas needed to understand so much about the natural world. Newton’s process of deriving Kepler’s laws and the universal law of gravitation helped secure the scientific method as an invaluable tool in our process of understanding the universe. Figure 2-15 shows some of the effects of gravity at the scales of planets, stars, and galaxies.
Insight Into Science: Quantify Predictions
Mathematics provides a language that enables science to make quantitative predictions that can be checked by anyone. For example, in this chapter, we have seen how Kepler’s third law and Newton’s universal law of gravitation correctly predict the motion of objects under the influence of the Sun’s gravitational attraction.
2-9 Frontiers yet to be discovered
The science related to forces and orbits described in this chapter was well established by the beginning of the nineteenth century. However, at least two questions remain: Why are the inertial mass (defined in Newton’s second law) and the mass used in his law of gravitation identical? Will the recent discovery of the Higgs boson stand up to repeated testing (part of the scientific method)?
64
65