11.4 11.3 The Banzhaf Model
You, along with 99,999 other voters, are deciding if your city should issue bonds to build a convention center. You will vote “yes,” but to pass the measure, a two-thirds majority is required. The Shapley–Shubik model would simply say that your power to influence the outcome is the same as that of any other voter, because each voter has the same chance to occupy the pivotal position (the 66,667th) in a voting permutation. Your Shapley–Shubik power index would be . The Banzhaf model focuses on the chance that you would cast the deciding vote. To pass, the measure must be approved by at least two-thirds—or 66,667—of the voters. You would cast the deciding vote if exactly 66,666 of the other voters were in favor of the measure. Otherwise, neither you nor anyone else will cast a deciding “yes” vote.
Coalition DEFINITION
A coalition is a set of participants in a voting system that might vote in favor of a measure. The empty coalition is allowed, and it represents a situation when the voters unanimously oppose a motion.
In the bond issue story, the set of voters in favor of passing the motion is a coalition. Your Banzhaf power index would be equal to the number of possible coalitions consisting of exactly 66,667 voters that you could belong to. Like the Shapley–Shubik power index, the Banzhaf power index would recognize that each voter has an equal chance to cast a decisive vote, but it counts the actual number of chances that a voter has to change the outcome.
In the voting permutation resulting from the 2012 United States presidential election, the pivotal voter was Pennsylvania (see Table 11.1 on page 468). But Pennsylvania did not cast a deciding vote. The Democratic ticket amassed 332 electoral votes, 62 votes more than the quota. If Pennsylvania’s 20 electors had been Republican, the Democratic ticket would have won anyway, with 312 electoral votes.
The states whose margin in favor of the Democratic ticket was greater than 1.000 formed the winning coalition in the 2012 presidential election.
Winning Coalition and Losing Coalition DEFINITION
A set of participants in a weighted voting system whose combined voting weight is equal to or greater than the quota is called a winning coalition. If the set of participants has a combined voting weight less than the quota, it is a losing coalition.
The Banzhaf model focuses on winning coalitions, and the essential voters within them. It is important to recognize that neither the Shapley–Shubik model nor the Banzhaf model are concerned with opinions of individual voters. Alice and Bill may not get along, but in the Shapley–Shubik model the permutations in which they are in consecutive positions are counted. In the Banzhaf model, if the coalition {Alice, Bill} is winning, it counts even if Alice and Bill always vote on opposite sides. The models are concerned only with the way the voting system distributes power.
475
A winning coalition may include some voters who are just along for the ride. If they were to desert the coalition, it would still win. The Banzhaf model counts the voters who are critical to its success.
Critical Voter DEFINITION
Let W be a winning coalition, and let V be a voter who belongs to W. Then V is a critical voter in W if the coalition consisting of all the voters in W except V is a losing coalition.
EXAMPLE 10 A Criminal Trial
After the evidence is presented and the summations are complete, the jury deliberates and each juror votes “guilty” or “not guilty.” We will regard these as two separate motions. Thus there is a “guilty” motion and a “not guilty” motion for each count that is before the jury. The jury must reach a unanimous verdict—there is only one winning coalition, the entire jury, and every juror is a critical voter. if neither “guilty” nor “not guilty” is approved in this system, a mistrial is declared, and the prosecution may demand a new trial.
In the landslide 1984 election the Republican ticket carried every state except one and had a total weight of 525, which was 255 votes more than the quota. There were no critical voters in the winning coalition, because any state could have switched to the Democratic ticket, and the Republican ticket would still have won. In the close election of 2000, the Republican ticket’s winning coalition had a total weight of 271 electoral votes, one more than the quota. All voters in the Republican coalition, except for the Nebraska congressional districts, were critical.
Self Check 11
Refer to Table 11.1 on page 468 to determine if any state was a critical voter in the 2012 election. Notice that a participant’s location in the voting permutation does not matter. You only need to check if the state was in the winning coalition, and if it was, did it have sufficient electoral votes to make a difference?
- No state was a critical voter. It is only necessary to see if California, which had the largest number of electoral votes in the winning coalition, was not a critical voter. The winning coalition had 332 electoral votes, 62 more than the quota. California had 55 votes, so the Democratic ticket would still win by a margin of 7 without California.
494
Banzhaf Power Index DEFINITION
In a weighted voting system, the Banzhaf power index of a voter V is the number of winning coalitions in which V is a critical member.
EXAMPLE 11 A Dictator
Consider the five-voter system . We’ll name the voters and , where stands for dictator. A set of voters is a winning coalition if and only if belongs to it. We can find the number of subsets of by applying the multiplication principle. Construct a subset by deciding if is in or out, two possibilities, and do the same for , , and . The number of subsets is . All of the winning coalitions consist of combined with one of these 16 subsets. in each winning coalition, is the only critical voter. Thus, has a Banzhaf index of 16, and I each of the other participants has a Banzhaf index of 0.
476
A dummy voter is one whose vote never makes a difference. A dummy voter is never a critical voter in any winning coalition, so its Banzhaf index is 0. In Example 11, were all dummy voters. Nevertheless, their presence increased the dictator’s Banzhaf power index—without them there would have been just one winning coalition, , and the dictator’s Banzhaf power index would have been 1.
Self Check 12
Find the Banzhaf index of each voter in the system .
The weight-4 voter is a dictator and is thus a critical voter in every winning coalition. Each winning coalition consists of the dictator and a subset of the three weight-1 voters. There are subsets of a three-element set—hence there are 8 winning coalitions. The dictator’s Banzhaf power index is therefore 8; the other voters are dummies, and their Banzhaf power indices are all 0.
Should Blocking Coalitions Be Counted? Spotlight 11.3
A voting combination is a list of the voters, recording how each voted. A voter is critical in a voting combination if a change in that voter’s vote, with no other voter switching, will change the outcome. The definition of the Banzhaf power index that we are using counts only a voter’s critical “yes” votes in a voting combination. However, Banzhaf’s original definitiona counted all voting combinations in which the voter was critical as a “yes” voter or as a “no” voter. Previous editions of this text used the original definition.
Let V be a voter, and suppose that V is a critical voter in b winning coalitions (so that according to the definition we are using, the Banzhaf power index of V is equal to b). Let W be one of the winning coalitions in which V is a critical voter, and let ҡ be the set formed by combining V with all of the voters who do not belong to W (see the figure).
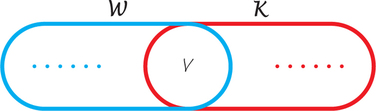
We will say that ҡ is a blocking coalition because, by voting “no,” it can prevent a motion from passing. Voter V is simultaneously a critical “yes” voter in the winning coalition W and, if she should change her vote, a critical “no” voter in the blocking coalition ҡ. Therefore, for each of the b winning combinations where V is a critical “yes” voter, there is a corresponding blocking combination—where V but no one else switches their vote—in which she is a critical “no” voter; there are b of these voting combinations, too. With the original definition, the Banzhaf index would be . Both indices yield the same distribution of voting power, but the original Banzhaf power index of each voter is double the index according to the definition that we are using.
Calculating the Banzhaf Index by Brute Force
The brute force way to compute the Banzhaf power index of a weighted voting system is to start with a list of all of the winning coalitions. Determine the total weight of each coalition by adding the weights of all the voters in the coalition. The total weight will be at least the quota because it is a winning coalition, so subtract the quota to obtain the extra votes that the coalition has.
Extra Votes DEFINITION
The extra votes of a winning coalition indicate the number of votes by which its total weight exceeds the quota.
477
When we know all of the winning coalitions and the extra votes that each has, we can identify the critical voters in each: They are the voters who belong to the coalition, and whose voting weights are more than the extra votes. For example, the winning coalition in the 2000 presidential election had one extra vote. Nebraska belonged to that coalition and had a voting weight of 2. Therefore, Nebraska was a critical voter in the coalition. The Nebraska first congressional district also belonged to the winning coalition, but it had a voting weight of only 1, and was therefore not a critical voter. Maine also had a voting weight of 2, but since Maine voted for the Democratic ticket, Maine was not a critical voter in the Republican coalition.
Grand Coalition DEFINITION
The grand coalition is the coalition that includes every voter.
In every voting system, the grand coalition is a winning coalition, because the quota must be less than or equal to the total weight of all of the voters.
EXAMPLE 12 The Banzhaf Model Applied to the Film Selection Committee
Let’s return to the committee of Example 4 on page 465. The members are Allen, Betty, and Cao, and they use the voting system. Let’s identify the critical voters in the grand coalition, {Allen, Betty, Cao}. if Allen leaves the coalition, what happens?
| Allen | Betty | Cao | Votes | Outcome |
|---|---|---|---|---|
| Yes | Yes | Yes | 9 | Pass |
| ↓ | ||||
| No | Yes | Yes | 4 | Fail |
Allen is a critical voter because the remaining voters form a losing coalition when he changes his vote. This is not surprising: He has veto power.
If Betty changes her vote, the remaining voters still form a winning coalition:
| Allen | Betty | Cao | Votes | Outcome |
|---|---|---|---|---|
| Yes | Yes | Yes | 9 | Pass |
| ↓ | ||||
| Yes | No | Yes | 6 | Pass |
Betty is not a critical voter in this coalition, and you can verify for yourself that Cao is also not a critical voter.
To determine the Banzhaf power indices of Allen, Betty, and Cao, refer to Table 11.4. The table lists all winning coalitions and the extra votes in each—that’s the total weight of the coalition minus the quota, 6. To obtain the list, the noncritical voters were removed, one by one, from the grand coalition. This yielded two winning coalitions, {Allen, Betty} and {Allen, Cao}. We cannot remove voters from these two coalitions without making losing coalitions, so we stop. The voters in each winning coalition with weight greater than the extra votes are the critical voters. We find Allen is critical in all three coalitions, while Betty and Cao are each critical in just one. Hence the Banzhaf index is (3, 1, 1).
478
| Critical Voters | |||||
|---|---|---|---|---|---|
| Coalition | Total Weight | Extra Votes | Allen | Betty | Cao |
| {Allen, Betty, Cao} | 9 | 3 | X | ||
| {Allen, Betty} | 8 | 2 | X | X | |
| {Allen, Cao} | 6 | 0 | X | X | |
Self Check 13
In Example 12, Allen was a critical voter in the grand coalition and he had veto power. Is it possible for a voter in a weighted voting system to be a critical voter in the grand coalition and not have veto power?
- No. Suppose that voter V is a critical voter in the grand coalition, and let be any coalition. If V does not belong to , then is a subset of the grand coalition with V removed, which we know is a losing coalition. Therefore, all winning coalitions must include V, and hence V has veto power.
The coalitions {Allen, Betty} and {Allen, Cao} are called minimal winning coalitions, because if one removes any voter the result will be a losing coalition.
Minimal Winning Coalition DEFINITION
A winning coalition is minimal if every voter who belongs to the coalition is critical in that coalition.
Self Check 14
Can the number of extra votes of a minimal winning coalition be greater than 0?
- Yes. In Example 12, we saw that {Allen, Betty} was a minimal winning coalition. It has 2 extra votes. The extra votes of a minimal winning coalition must be less than the voting weight of each member of the coalition.
To make a complete list of all of the winning coalitions in a weighted voting system, start with the grand coalition. Step 1 is to form new winning coalitions by removing noncritical voters, one at a time, from the grand coalition. The number of winning coalitions formed in Step 1 is equal to the number of members of the grand coalition who are not critical voters. This is the procedure that was followed in Example 12. If some of the winning coalitions formed in Step 1 are not minimal, Step 2 is to remove noncritical voters, one at a time, from each of the winning coalitions obtained in Step 1. If some of the winning coalitions created in Step 2 are not minimal, proceed with them as in Step 2. The process ends when it cannot continue, because all of the winning coalitions formed in the last step were minimal.
You must be careful not to list any winning coalition more than once. This is illustrated in the following example.
EXAMPLE 13 A Five-Voter System
use the weighted voting system . List the winning coalitions and find their critical voters.
We will start with the grand coalition. it has a total weight of 19, so there are 7 extra votes. Since no voter has more than 7 votes, the grand coalition has no critical voters.
479
Step 1 is to remove members of the grand coalition one at a time and obtain five winning coalitions: (0 extra votes, a minimal winning coalition); and (3 extra votes each; all voters except and are critical); (4 extra votes, only is critical); and (5 extra votes, only is critical).
Step 2 is to remove noncritical voters from the winning coalitions found in Step 1. We obtain , a minimal winning coalition with 0 extra votes, by removing from or by removing from . Only count this once! By removing from or from , one gets . In the same way, there are two ways to get the minimal winning coalitions and from and one other four-member coalition listed above. Finally, the minimal winning coalition can be obtained from or by removing the last voter from either one.
Table 11.5 summarizes the results and determines the Banzhaf power index of each participant. There are 11 winning coalitions in all. When compared with 120 permutations for the Shapley–Shubik index, it is manageable.
| Critical Votes | ||||||
|---|---|---|---|---|---|---|
| Coalition | Extra Votes | |||||
| 7 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 1 | 1 | |
| 3 | 1 | 0 | 1 | 0 | 0 | |
| 3 | 1 | 1 | 0 | 0 | 0 | |
| 4 | 1 | 0 | 0 | 0 | 0 | |
| 6 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | 1 | |
| 2 | 1 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 1 | |
| 2 | 1 | 1 | 0 | 1 | 0 | |
| 3 | 1 | 1 | 1 | 0 | 0 | |
| Banzhaf power index | 9 | 5 | 5 | 3 | 3 | |
Self Check 15
Show the other ways to get the minimal winning coalitions and .
- You could get by removing from , and by removing from .
Combinations
480
In Alice’s committee (see Example 7 on page 472), Alice has voting weight 3, and there are eight other members with voting weight 1. The quota is 6, so the voting system is. In calculating the Shapley–Shubik power index, it was helpful that the members, except for Alice, were equally weighted. We would like to make use of this feature in determining the Banzhaf power index, too. There are differences, though: Unlike the Shapley–Shubik power indices, which always sum to 1, the Banzhaf power indices have no fixed sum. Therefore, one cannot determine the Banzhaf power indices of the other participants, after Alice’s index is known, without further calculation. A second difference has to do with permutations versus combinations. The Shapley–Shubik power index is based on counting permutations, which are different ways of ordering all of the members of a set. The Banzhaf index is based on counting winning coalitions, which are different subsets of the grand coalition. When counting subsets of a given set, we are dealing with combinations.
Algebra Review Appendix
Combinations
A Real Mathematical Quagmire Spotlight 11.4
The U.S. Supreme Court, in its 1962 decision of the case Baker v. Carr, instituted a principle that legislative districts within states should be equal in population. The decision was based on the “Equal Protection” clause of the Fourteenth Amendment to the U.S. Constitution. Dissenting, Justice Frankfurter declared that the process of equalizing populations would lead to a “mathematical quagmire.”
The decision had repercussions for state and county legislative districts throughout the United States. Some district boundaries were redrawn to equalize populations. To avoid redrawing district boundaries the New Jersey legislature, the New York City Board of Estimate, Nassau County, and several other county boards of supervisors in New York State resorted to weighted voting, where the voting weight of a legislator (or supervisor) would be roughly proportional to the population being represented.
In a 1965 law review article, John F. Banzhaf iii pointed out that three of the six supervisors of Nassau County, New York, were dummy voters (see Example 3 on page 464). in the same article he argued that the weighted voting system employed by the New Jersey legislature was unfair. The article inspired legal action against several elected bodies that employed weighted voting systems.
A lawsuit invalidated the voting system of the Board of Supervisors of Washington County, New York, in 1967. in its decision, the New York State Court of Appeals provided a way to fix a weighted voting system: Each supervisor’s Banzhaf power index, rather than his or her voting weight, should be proportional to the population of the district that he or she represents. Borrowing Justice Frankfurter’s phrase, the Court predicted that its remedy would lead to a “mathematical quagmire.”
Five lawsuits filed over a period of 25 years challenged weighted voting in the Nassau County Board of Supervisors. Thus, the mathematical quagmire that the appeals court had feared actually materialized. Although Nassau County made a sincere attempt to comply with the Washington County decision, every voting system that it devised faced a new lawsuit. With conflicting expert testimony, the U.S. District Court finally ruled in 1993 that weighted voting was inherently unfair.
Banzhaf’s article was aptly titled “Weighted Voting Doesn’t Work.” (it, and the Washington County decision, are included in the Suggested Readings at the end of this chapter. The Nassau County quagmire is the subject of Exercise 5 on page 496. You can explore what happened to the Board of Estimate in Exercises 38 and 39 on page 499).
Let’s see how we would determine Alice’s Banzhaf power index. She would be a critical voter in any winning coalition that has less than 3 extra votes. She would need to join with at least three of the other members to meet the quota, but with less than six of the others. Thus, she needs to assemble a subset of the other eight members consisting of three, four, or five members. The number of ways to choose three members of a set of eight is given the symbol . You may pronounce it “eight choose three.”
Combinations and Combinations Symbol DEFINITION
The combinations symbol stands for the number of ways to choose members from a set of elements—that is, the number of combinations of objects, taken at a time.
481
For example, because there is just one way to get zero elements from a set of , independent of . If we are selecting one element from a set of , there are obviously ways to do it, so . We can determine a formula for by considering a toast in which each guest clinks glasses with each other guest. The number of “clinks” is . If I’m a guest, I will clink with others. Each of the guests will do that, so multiply and divide by 2, because we’ve counted every “clink” twice. (For example, I clink with you, and you clink with me, but that is just one “clink.”) Thus
Alice’s Banzhaf power index is . Fortunately, there is a simple formula for .
Formula 1: Basic Combinations Formula FORMULA
Formula 1 holds, provided and are whole numbers and are not negative. We can apply it to calculate if we remember that :
EXAMPLE 14 Calculate
By formula 1, . Using ; , and ; we get .
This is not how we should calculate combinations, because it is more efficient to cancel before multiplying. The first cancellation is
Then
Using the cancellation trick, and , we get a simple way to verify .
Self Check 16
Use Formula 1 to verify that .
Self Check 17
Calculate and without using a calculator.
482
EXAMPLE 15 Banzhaf Power in Alice’s Committee
Alice’s Banzhaf index has already been determined: It is .
Bill, a weight-1 participant, will be a critical voter in any winning coalition with exactly 6 votes. He will need, in addition to his own vote, Alice’s vote and the votes of two other participants, or, without Alice, he will need the votes of five other participants. He must get the two or the five votes from the seven other weight-1 participants—he can’t vote twice!
There are winning coalitions in which Bill casts a critical vote and Alice is included, and winning coalitions where Bill casts a critical vote and Alice is not included. Bill’s Banzhaf power index is . The other participants have the same index.
By the Banzhaf model, Alice is times as powerful as Bill. This is reasonably close to the Shapley–Shubik model’s assessment that Alice is 4 times as powerful as Bill.
You have probably noticed that , and . If you suspect that there is symmetry here, you are right.
Formula 2: Symmetry of Combinations FORMULA
We have seen that Formula 2 holds for and —it would have saved a bit of time in calculating and .
There are two ways to verify this formula. One is to consider a coalition of members from a committee with members. The members vote “yes” and the remaining members vote “no.” There are such coalitions. Now suppose everyone reverses his or her vote. If that happens, there are “nays” and “yeas,” corresponding to a coalition with members. There are of these coalitions. The coalitions of members from a set of can therefore be matched, one to one, with the coalitions of members from the set of members.
Self Check 18
Use Formula 1 to verify Formula 2.
In Example 9 (page 473), we saw that, according to the Shapley–Shubik model, Alice’s power was cut in half when three members of the committee agreed to cede their votes to Bill. In the next example, we will explore this situation in the context of the Banzhaf model. Writing Project 1 (page 501) provides an opportunity to explore the effect of a pact between states in the Electoral College that might have a similar effect.
483
EXAMPLE 16 The Revolt: Banzhaf Model
In Example 9, Alice’s committee was transformed to a weighted voting system by a pact in which three weight-1 voters agreed to let Bill have their votes. Alice will be a critical voter in any winning coalition when she is joined by a losing coalition with weight 3, 4, or 5. This losing coalition could be Bill alone or Bill joined by one weight-1 voter, or it could be three or all four weight-1 voters. There is coalition consisting of Bill alone, and coalitions with Bill and one weight-1 voter. There are coalitions of three or four weight-1 voters, so Alice’s Banzhaf index is .
Bill will be a critical voter in any winning coalition when the other voters have a total weight of 2, 3, 4, or 5. These other voters could be Alice plus up to two weight-1 voters; there are of these coalitions. Without Alice, Bill would need two or more weight-1 voters; there are such coalitions, so Bill’s Banzhaf index, 22, is more than twice Alice’s.
A weight-1 voter, Zoë, must be joined by other voters with total weight 5 to form a winning coalition in which she is critical. That could be Alice and two of the three other weight-1 voters; there are of these coalitions. if Zoë is joined by Bill, exactly one of the three other weight-1 voters is needed. There are three of these coalitions too, so Zoë’s Banzhaf index is 6.
One way to compare the Banzhaf indices between the two committees is to assign to each participant his or her share of the critical votes. Thus, in the committee as structured in Example 15, one participant (Alice) has 182 critical votes, and the eight weight-1 voters each have 42 critical votes. In all, the members of the committee have between them critical votes. Alice’s share of the crucial votes is , while each weight-1 voter has of the critical votes.
After the pact, as in Example 16, Alice has 10 critical votes, Bill has 22, and four weight-1 participants each have 6, for a total of critical votes. Now Alice has of the critical votes, Bill has of the critical votes, and each of the four remaining weight-1 voters has of the critical votes.
Probability of Casting a Critical Vote
Unless a voter has veto power or is a dummy voter, it is not realistic to use a power index to measure his or her ability to influence the outcome of an election. Many factors—such as politics, for example—are not addressed by these models. Suppose that a voter, Charles, wants to know the probability that his “yes” vote will be critical. The Banzhaf model can answer this question, under the assumption that the other voters are not influenced by Charles or anyone else. We will therefore assume that each voter except Charles will toss a coin: heads for yea, tails for nay.
The probability that Charles will cast a critical vote is equal to
484
The numerator of this fraction is Charles’s Banzhaf power index. To determine the denominator, let be the number of voters. Each coalition that includes Charles also includes a subset of the other participants—the ones that got heads when they tossed their coins. We can count the coalitions that include Charles by determining how many outcomes are possible if people each toss a coin. Since each person has two possible outcomes, the answer is
Therefore, the probability that Charles is a critical voter is equal to
The Electoral College: Presidential Elections of 2012, 2016, and 2020 Spotlight 11.5
The table below displays the Shapley-Shubik (SSPI) and Banzhaf (BPI) power indices of the voters in the Electoral College, as compared with the voter’s weight as a percent of 538 (PCT), the total weight of all the voters. It shows that for the most part both measures of power agree closely with the actual share of power that a participant in the college has by virtue of its voting weight. There is an exception, though. California, whose voting weight is slightly more than 10% of 538, has more than its share of power by either measure. The power indices shown were calculated with the online Power Index Calculator (see page 502).
| Voting Weight | Voters with This Weight | PCT (%) | SSPI (%) | BPI (%) |
|---|---|---|---|---|
| 55 | CA | 10.22 | 11.03 | 11.36 |
| 38 | TX | 7.06 | 7.32 | 7.21 |
| 29 | NY, FL | 5.39 | 5.51 | 5.43 |
| 20 | IL, PA | 3.72 | 3.72 | 3.68 |
| 18 | QH | 3.35 | 3.33 | 3.30 |
| 16 | GA, MI | 2.97 | 2.95 | 2.93 |
| 15 | NC | 2.79 | 2.76 | 2.74 |
| 14 | NJ | 2.60 | 2.57 | 2.74 |
| 13 | VA | 2.42 | 2.38 | 2.37 |
| 12 | WA | 2.23 | 2.20 | 2.19 |
| 11 | AZ, IN, MA, TN | 2.04 | 2.01 | 2.01 |
| 10 | MD, MN, MQ, WI | 1.86 | 1.82 | 1.82 |
| 9 | AL, CQ, SC | 1.67 | 1.64 | 1.64 |
| 8 | KY, LA | 1.49 | 1.45 | 1.45 |
| 7 | CT, OK, QR | 1.30 | 1.27 | 1.27 |
| 6 | AR, IA, KS, MS, NV, UT | 1.12 | 1.09 | 1.09 |
| 5 | NM, WV | 0.93 | 0.90 | 0.91 |
| 4 | HI, ID, NH, RI | 0.74 | 0.72 | 0.73 |
| 3 | AK, DE, DC, MT | 0.56 | 0.54 | 0.55 |
| 3 | ND, SD, VT, WY | 0.56 | 0.54 | 0.55 |
| 2 | ME, NE | 0.37 | 0.36 | 0.36 |
| 1 | ME, NE congressional districts | 0.19 | 0.18 | 0.18 |
485
EXAMPLE 17 The Jury
A jury of 12 members must reach a unanimous verdict. This means that the only winning coalition is the grand coalition. The Banzhaf power index of each member of the jury is 1. Thus the probability that a juror will be a critical voter is . One might think that most criminal trials would end as mistrials, since it is so unlikely that the jurors would agree. But the Banzhaf model only touches on the voting system. it does not consider all of the evidence that the jurors see before they vote.
EXAMPLE 18 Majority Rule
A committee uses majority rule. What is the probability that a member of the committee will cast a critical vote in a winning coalition? Since every voter has weight 1, no one is a critical voter in a winning coalition unless the coalition has 0 extra votes; it must be a minimal winning coalition.
If there are three members, , , and , then the minimal winning coalitions with are and . The Banzhaf power index of is 2, so the probability that will be critical is
With four voters, the minimal winning coalitions will have three members. would have to be joined by two of the other three members, so ’s Banzhaf power index is . The probability that will be critical is .
If the number of voters is even, say , then a minimal winning coalition has members. Voter would be joined by of the other members to form a minimal winning coalition. The Banzhaf power index of would be and the probability that will be a critical voter is
With an odd number of voters a minimal winning coalition would still have members. Voter would be joined by of the other voters to form a minimal winning coalition, so the Banzhaf power index of would be , and the probability that is critical would be
Table 11.6 shows a few of these probabilities.
| 1 | 100.0% | 10 | 24.61% | 1,000 | 2.523% |
| 2 | 50.0% | 11 | 24.61% | 2,000 | 1.784% |
| 3 | 50.0% | 20 | 17.62% | 10,000 | 0.564% |
| 4 | 37.5% | 21 | 17.62% | 20,000 | 0.399% |
| 5 | 37.5% | 100 | 7.96% | 100,000 | 0.252% |
| 6 | 31.2% | 101 | 7.96% | 1,000,000 | 0.056% |
Table 11.6 reveals some unexpected features. First, it appears that the probability that a voter will cast a critical vote when there is an even number of voters is the same as when there are voters! This phenomenon can be explained by using the sum formula for combinations.
486
Formula 3: Sum Formula for Combinations FORMULA
Here’s why the sum formula works: Suppose you are involved in a voting system with voters. The number of combinations with voters is . Of these, coalitions do not include you. Any coalition that you belong to also has of the other voters; there are of these coalitions. Adding these numbers, we obtain the above sum formula.
By the sum formula, . By symmetry (Formula 2), . Combining these equations, we get
The probability of casting a critical vote when there are voters is , and the probability of casting a critical vote in a -voter system is also equal to
The second interesting feature of Table 11.6 is that while a voter’s chance of casting a critical vote decreases as the number of voters increases, the rate of decrease is slow. One would not think there would be much chance of casting a critical vote in a system with a million voters, but the chances are better than 1 in 2000. When the number of voters is large (hundreds or more), it is not practical to use the combination formula (Formula 1) to determine and then divide by because these numbers will be unmanageably large. Instead, use an approximation.
Formula 4: An Approximation FORMULA
is approximately equal to
In this formula, which can be derived using calculus, is the ratio 3.14159 . . . of the circumference of a circle to its diameter. The approximation is not too bad even if , and improves as increases.
Self Check 19
Use Formula 4 to approximate the probabilities for the even values of in the first two columns of Table 11.6. Compare your results with the probabilities given in the table (which were calculated using Formula 1, not the approximation). Don’t bother with the third column because Formula 4 was used to compute those probabilities.
Approximation Approximation 2 50.0% 10 24.61% 4 37.5% 20 17.62% 6 31.2% 100 7.96%
487
Can the Banzhaf and Shapley-Shubik Models Disagree? Spotlight 11.6
In Self Check 9 (page 472) you calculated the Shapley- Shubik index of a 90-voter system in which Alice had 30 votes and the other 89 voters each had 1 vote apiece, where the quota was a simple majority, 60. You found that Alice had a Shapley-Shubik index of , just as in the committee with voting system . According to the Banzhaf model Alice had a slightly larger share of the power (about 35%) in the nine-voter system. You are not expected to calculate the Banzhaf index of the 90-member committee, because—while it is simple to do so in principle— the arithmetic is hard to manage. Alice will be a critical voter in any winning coalition when joined by between 30 and 59 of the other voters. There are
Algebra Review Appendix
Scientific Notation
of these coalitions, and this is her Banzhaf index. Expressed in scientific notation, Alice’s Banzhaf index is approximately . A weight-1 voter will be critical when joined by Alice and 29 other weight-1 voters or by 59 weight-1 voters. This voter’s Banzhaf index is . This is a pretty big number too, approximately , or about the number of molecules in 9 milliliters of water (nearly 2 teaspoons). Alice’s Banzhaf index is 2043 times as large, comparable to the number of molecules in 18.5 liters (about 5 gallons) of water. in the 90-member committee, the models differ radically. Let’s use the water analogy to measure this. Alice has 18.5 liters, each of the 89 weight-1 voters has 0.009 liters. The sum of all the Banzhaf indices is liters. Alice’s share is of the power according to the Banzhaf model, but 33.3% of the power in the Shapley-Shubik model.
How can we explain this difference? With the Shapley-Shubik model, Alice is a pivot if she is in one of 30 places in a permutation that has 90 places. Hence she has one-third of the power. For the Banzhaf index, suppose Alice votes “yes” and each of 89 weight-1 voters tosses a coin. What is the probability that between 29 and 59 of the tosses is heads? The average number of heads is 44.5, and it’s very unlikely that the total number of heads will be more than 15 away from that value. A weight-1 voter will be critical if 29 of the other 88 weight-1 voters, and Alice, throw heads, or if 59 of the other weight-1 voters throw heads and Alice throws tails. This is improbable, because on the average there will be 44 heads when 88 coins are thrown, and it will not be often that the number of heads will be exactly 15 more or less than 44.