EXAMPLE 4 What About a 10-Foot Steel Cube?

What is the pressure on the bottom of a steel cube 10 ft on a side?

If we scale the original cube of steel up to a cube that is 10 ft on a side, then the total volume is

The weight of the cube is

The area of the bottom face is

The pressure on the bottom face is

This is 10 times—not “10 times more than”—the pressure on the bottom face of the original 1-ft cube.

What would be the pressure on the bottom face of a steel cube 100 ft on a side? Be sure to give not just a number but also the correct units for the answer.

EXAMPLE 5 What About Burj Khalifa?

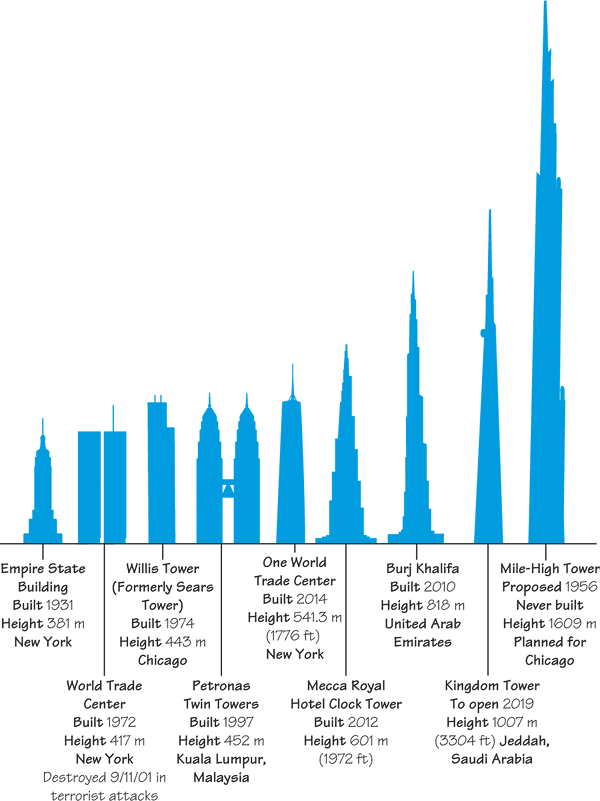
Burj Khalifa in Dubai (see Figure 18.6), completed in 2010, is still the world’s tallest skyscraper at 2684 ft (how much is that in meters?), not counting radio and television antennas (see Spotlight 18.1). What is the pressure at the bottom of its walls?

The building is made of reinforced concrete, which weighs . Although the building tapers toward the top, we are not far off if we model it as straight up and down—that is, as a rectangular solid. Consider one of its supporting walls. The volume of the wall is its height times the area of its base, or . The weight of the wall is . The pressure at the bottom from the wall’s weight is

where we have rounded off the calculated answer to agree with the degree of precision of the ingredient numbers.

That’s not counting the contents of the tower, which also must be supported.

In 1956, the famous American architect Frank Lloyd Wright (1867–1959) proposed a mile-high “Illinois Sky- City” tower for the Chicago lakefront. Burj Khalifa, at 2684 ft, is just over half that high. In the text, we focus on the problem of holding up the weight of such a structure.

But there are other limits to the height of a building— for example, the bending of the building in the wind, which can go up dramatically with height. Bending can be controlled by making the building stiffer.

The terrorist destruction of the World Trade Center towers in 2001 resulted not directly from the aircraft impacts but from the subsequent fires and collapse of the towers’ structure.

Even if designed to better resist fires and impacts, however, a mile-high building might not be practical. For example, the enormous number of people (perhaps 100,000) living, working, or visiting in such a building would create enormous traffic problems (pedestrian, parking, deliveries) for blocks around.

Cost per square foot of usable area is an important consideration. Even if the building did not taper, the space in the upper floors might not justify their additional expense. With increasing height, an increasingly larger proportion of the cross-sectional area of all floors must be devoted to services, such as elevators; everyone entering the building and going to any floor needs to start in an elevator on the ground floor. In an emergency evacuation, the people must walk downstairs! And that could take dangerously long.

Some architects, however, maintain that the main limit on the height of a building is human physiology. Differences in air pressure between the top and bottom of a building limit how fast elevators can rise or drop without discomfort to passengers, thereby enforcing long travel times for “vertical commuters.” Human psychology also might present some limits.

Are skyscrapers now dinosaurs, except as exercises in one-upmanship—“vertical cities for the affluent,” as Blaine Brownell of the University of Minnesota School of Architecture calls them? Telecommuting and outsourcing of work to decentralized locations may make it obsolete to bring office workers together at a single site in a dense, expensive downtown.

In 2012, renowned science fiction writer Neal Stephenson, together with structural engineer Dr. Keith Hjelmstad, designed a tower 20 km (over 60,000 ft) high. The base would be 10 mi wide, the building would require one billion tons of steel (half the annual output of the world), and the cost would be $1 trillion. Said Hjelmstad, it “would be the biggest project ever undertaken by humans.” It would be a convenient launching pad for sending payloads into orbit and beyond.

Guess what they found to be the biggest hurdle? Not the challenge of building it, nor the fact that it would be in the way of airliners, but handling the jet stream—which at that height can gust to 310 mph. So the project is “on pause.”

Meanwhile, Stephenson has written a science fiction story about an engineer trying to build such a building: “Atmosphera incognita,” in Hieroglyph: Stories and Visions for a Better Future, edited by Ed Finn and Kathyrn Cramer (William Morrow, 2014), 1–37.

Consider the possibility of a Super Burj Khalifa 10 times as high. How much weight would the bottom of its walls have to support per square foot?

EXAMPLE 6 How High Can a Mountain Be?

Just like skyscrapers, the height of mountains is also limited, by gravity, their composition, and their shape. How tall can a mountain be?

We build a simple mathematical model of a mountain. Suppose that it is made of granite, a common material, with uniform density. Granite weighs and has a crushing strength of about 4 million .

In the interests of both realism and simplicity, we assume that the mountain is a solid cone whose width at the base is the same as its height. Let’s model Mount Everest, the tallest mountain on Earth, at about 6 mi high. The base, then, is a circle with a diameter (distance across) of 6 mi. The radius (half the diameter) is 3 mi (Figure 18.7). Because we took round numbers (6 mi) for the height and width, we record as significant only the first digit or two of the results of the calculations.

What does the model Everest weigh? The relevant formula is , or

We already know the density of granite , so to find the weight, we need the formula for the volume of a cone of radius and height :

Using a radius of 3 mi and a height of 6 mi, we find that the model Everest has a volume of about .

751

To find the weight of of granite, we need to convert units because the density that we know is in pounds per cubic foot . Let’s convert to units of feet as follows:

Thus,

So we have

Now that we know the mountain weighs 1.4 quadrillion pounds, we want to find the pressure on the base of the cone and compare it with the crushing strength of granite. (Everest is standing, so if our model is any good, that pressure will be below the crushing strength.)

Physics tells us that the weight of the mountain is spread evenly over the base of the cone (though we are oversimplifying the geology underlying mountains). Because

we need to calculate the area of the base of the cone. The shape is a circle, and the familiar formula

gives for a radius mi an area of .

Once again, we need to convert units to express the pressure in pounds per square foot, the units in which the crushing strength is expressed. We get

Then

This number is about half the crushing strength of granite, . For a mountain to come close to the limitation of the crushing strength of granite, it would have to be only about 10 mi high, not quite twice as high as Everest. Other physical considerations suggest a maximum height of at most 15 mi. The fact that no current mountains are that high may be a consequence of the Earth’s high amount of volcanic activity and the structural deformation of the Earth’s crust. For a mountain that is too big, the rock below it would flow and the mountain would sink.

EXAMPLE 7 How Tall Can a Tree Be?

Galileo suggested that no tree could grow taller than 300 ft. The world’s tallest trees are giant sequoias (Figure 18.8), which grow only on the West Coast of the United States and hence were unknown to Galileo. The tallest known sequoia today is 380 ft in Redwood National Park in Northern California. (To protect it, the National Park Service does not disclose its exact location.)

What limits the height of a tree? If the roots do not adequately anchor it, a tall tree can blow over. (This happened in 1990 to the world’s then-tallest tree, the Dyerville Giant in Humboldt Redwoods State Park in California.) The tree could buckle or snap under its own weight and the force of a strong wind. The wood at the bottom can be crushed if there is too much weight pressing upon it. Finally, there is a limit to how far the tree can lift water and minerals from the roots to the leaves.

Could a tree be a mile high? To make a rough estimate of the pressure at the base of the tree due to gravity, let’s model the tree as a perfectly vertical cylinder. Over each square foot at the bottom, there are of cells of wood, which weighs about half as much as water. A convenient scientific fact to know involving the metric system is that water weighs just about 1 gram (g) per cubic centimeter. So, to calculate the weight, we first translate into metric measurement:

So, of water weighs about

Consequently, of water weighs about . The weight of the same volume of wood is about half as much, or about 165,000 lb. Therefore, the pressure at the bottom of the tree would be about .

This is an overestimate because we assumed that the tree does not taper. A tree that tapers steadily looks like an elongated cone; using a more realistic cone model (as we did in the last section for a mountain), you would find that the pressure at the bottom of the tree would be one-third of , or about . A biological organism needs a safety factor of at least 2 to 4 times the absolute minimum physical limits, so a mile-high tree would need from 110,000 to of upward pressure for water and minerals. Tension in the string of water molecules from root to leaf ranges from 80,000 to 3.2 million , for different kinds and heights of trees, so this consideration does not rule out mile-high trees.

753

At more than about , though, the bottom of the tree would begin to crush under this weight. On this basis, a mile-high tree is barely feasible, with little margin of safety. However, researchers who hauled themselves up to the top of the tallest trees in 2004 found a much lower limit, at least for giant sequoias. With increasing height, leaves are smaller, dryer, and less efficient at photosynthesis. The researchers estimated that trees can’t top out higher than 400 to 427 ft. The tallest reliably measured tree was a North American Douglas fir, measured in 1902 at 413 ft.

There are other considerations. The taller the tree, the greater the area from which it must draw water and minerals, for which nearby trees also compete. Moreover, for a tree to grow very tall, it would have to live for a very long time. Evolution and time may select against extremely tall trees, or maybe, for no reason at all, they have just never evolved.

The size of some animals is astonishing to us. A blue whale can be 100 ft long and weigh 200 tons. Land- dwelling dinosaurs of 200 million years ago may have been almost as large.

Why so big? To be tall has advantages: A tall tree can gather more sunlight; a giraffe can harvest leaves that other herbivores can’t reach; and a dog is more likely to be submissive to another dog or person who is taller. In the case of people, taller can be more attractive: Studies indicate that taller men earn more money, and women make themselves look taller by wearing high heels.

Sheer bulk and muscle can have its advantages, as when male bighorn sheep or red deer wrestle for dominance and the right to sire offspring. And a larger size can make it easier for an animal to defend territory.

But apart from intraspecies (within species) differences, what could be the advantage of being larger than other species?

A full-grown and healthy wildebeest is less likely to be eaten by predators; but a hippopotamus, a rhinoceros, or an elephant—which are all even bigger—are even less likely to become victims.

There are some gains in “efficiency” in being large. The metabolic rate goes down, which means that a species twice as large does not require quite twice as much food. A larger species can have a more complex digestive system, so it can eat a broader array of foods—or simply different foods—than smaller species.

A large animal needs a thick hide to hold in its bulk, and such a hide can also provide thermal insulation, allowing the animal to live in a colder climate.

Of course, there are also disadvantages to size. Really big birds, such as ostriches, emus, or even penguins, can’t fly—but maybe they don’t need to: Ostriches can run fast, and penguins can swim. A large animal can’t easily take shelter under a small tree or hide by digging a burrow. Large animals tend to reproduce more slowly, with longer gestation periods (two years for an elephant) and smaller litters (with even twins rare). The biggest challenge is finding enough food; whales migrate to do so.

But why did some animals become large, even gigantic? They adapted and evolved to fit an open ecological niche, and becoming large aided their fitness for that niche. When that niche disappeared—the steamy plant jungles in the case of dinosaurs, the Great Plains of grasses in the case of American buffalo—the animals did, too.