19 Symmetry and Pattern

19.1 Symmetry and Pattern 19

779

19.1 Fibonacci Numbers and the Golden Ratio
19.2 Rosette and Strip Patterns
19.3 Notation for Patterns
19.4 Symmetry Groups
19.5 Fractal Patterns and Chaos

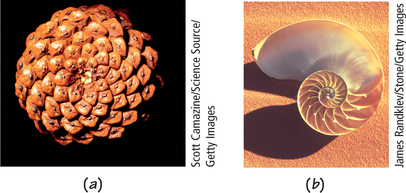
What is symmetry? You may think symmetry refers just to a mirror-image reflection, such as between the sides of the human body. But you also sense symmetry in rotations, as in the two-dimensional spirals in the beauty of daisies and sunflowers (Figure 19.1) and even in three-dimensional form on pineapples, pinecones, sunflowers, and cacti (Figure 19.2a).

The chambered nautilus (Figure 19.2b) may stretch your notion of symmetry (as will other examples in this chapter). It has neither reflection nor rotational symmetry, but its successive sections are geometrically similar (in the sense of Chapter 18: same shape but different size), and the resulting spiral has the same shape at any size: A photographic enlargement superimposed on it would fit exactly.

Figure 19.1: Figure 19.1 (a) This daisy has in its center 21 spirals clockwise and 34 spirals counterclockwise. (b) This heart of a sunflower has 34 spirals clockwise and 55 spirals counterclockwise.

Figure 19.2: Figure 19.2 (a) Spirals of scales on a pinecone: 8 right, 13 left. (b) A chambered nautilus shell.

780

In a broad sense, symmetry includes notions of repetition but also balance and proportionality (geometric similarity).

What is the connection of mathematics to the beauty and symmetries that we observe in nature? Mathematics is the science of patterns; it allows us to identify, classify, and appreciate more deeply different kinds of symmetry.

A simple number pattern is related both to the symmetric spirals in plants and to a proportion that offers a standard of beauty. The formula for calculating that proportion is also used in the Consumer Price Index (CPI) and was critical in formulating the standard for high-definition television (HDTV).

What does it mean for a pattern to be symmetrical, that is, have copies of a design element (“motif”) arranged in a symmetrical way? Utterly surprising is that though there is an infinite variety of motifs, there are very few symmetrical patterns for arranging copies of one. We illustrate these patterns and provide (in Section 19.3) notation, decision trees, and examples.

Symmetries of a pattern can be thought of as geometric transformations that preserve a pattern, and they interact among themselves to generate further symmetries.

Finally, what happens if we scale a design element down (or up) in size as part of the notion of symmetry? Along with the chambered nautilus, we get fractals, with their own symmetry and beauty.