Chapter 20 Exercises
Chapter 20 Exercises
Hint: For the exercises about determining whether a shape can tile the plane, you should make copies of the shape and experiment with placing them. One easy way to make copies is to trace the shape onto a piece of paper, staple half a dozen other blank sheets behind that sheet, and use scissors to cut through all the sheets along the edges of the traced shape on the top sheet.
20.1 Tilings with Regular Polygons
Question 20.31
1. Determine the measure of an exterior angle and of an interior angle of a regular dodecagon (12 sides).
1.
Exterior: 30°; Interior: 150°
Question 20.32
2. Determine the measure of an exterior angle and of an interior angle of a regular decagon (10 sides).
Question 20.33
3. Specify a formula for the measure of an interior angle of a regular -gon.
3.
Question 20.34
4. Using the formula from Exercise 3 and a calculator, make a table of the interior-angle measures of regular polygons with 3, 4, …, 12 sides.
Question 20.35
![]() 5. Use the table of interior-angle measures from Exercise 4 to determine all the possible vertex types of regular polygons (with at most 12 sides) surrounding a point.
5. Use the table of interior-angle measures from Exercise 4 to determine all the possible vertex types of regular polygons (with at most 12 sides) surrounding a point.
5.
The usual notation for a vertex type is to denote a regular -gon by , separate the sizes of polygons by periods, and list the polygons in clockwise order starting from the smallest number of sides, so that, for example, 3.3.3.3.3.3 denotes six equilateral triangles meeting at a vertex. The possible vertex types are 3.3.3.3.3.3, 3.3.3.3.6, 3.3.3.4.4, 3.3.4.3.4, 3.3.4.12, 3.4.3.12, 3.3.6.6, 3.6.3.6, 3.4.4.6, 3.4.6.4, 3.12.12, 4.4.4.4, 4.6.12, 4.8.8, 5.5.10, and 6.6.6.
Question 20.36
![]() 6. Which of the vertex types of Exercise 5 do not occur in a semiregular tiling?
6. Which of the vertex types of Exercise 5 do not occur in a semiregular tiling?
Question 20.37
![]() 7. In addition to the vertex types of Exercise 5, Xîp** exactly five others are possible, each involving one polygon with more than 12 sides. None of these vertex types leads to a semiregular tiling. The five many-sided polygons involved in these five vertex types have 15, 18, 20, 24, and 42 sides. Determine the other polygons in each of these five vertex types.
7. In addition to the vertex types of Exercise 5, Xîp** exactly five others are possible, each involving one polygon with more than 12 sides. None of these vertex types leads to a semiregular tiling. The five many-sided polygons involved in these five vertex types have 15, 18, 20, 24, and 42 sides. Determine the other polygons in each of these five vertex types.
7.
3.7.42, 3.9.18, 3.8.24, 3.10.15, and 4.5.20
For Exercises 8 and 9, refer to the second tiling in the bottom row of Figure 20.4 on page 831, which shows a tiling by isosceles triangles.
Question 20.38
8. Use the center of the tiling to determine the measures of the angles of the isosceles triangle tile.
859
Question 20.39
9. Every vertex except the center vertex has the same vertex type, in terms of the measures of the angles surrounding the vertex. What is that vertex type?
9.
At each of the vertices except the center one, six triangles meet, with angles (in clockwise order) of 75°, 75°, 30°, 30°, 75°, and 75°.
20.2 Tilings with Irregular Polygons
Question 20.40
10. For each tile below, find a tiling of the plane. (Adapted from Branko Grünbaum and G. C. Shephard, Tilings and Patterns, W. H. Freeman, New York, 1987, p. 25.)
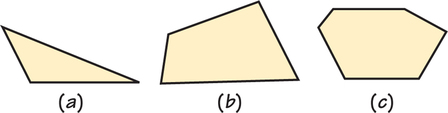
Question 20.41
11. You know that a regular pentagon cannot tile the plane. Suppose that you cut one in half into two mirror- symmetric pieces. Can this new shape tile the plane? (See Figure 19.4 on page 787 for a regular pentagon that you can trace.)
11.
Yes
Question 20.42
![]() 12. Design a nonconvex hexagon that can tile the plane.
12. Design a nonconvex hexagon that can tile the plane.
Question 20.43
![]()
 13. If you “unbulge” an ordinary soccer ball so that each of its sewn pieces is flat, you get a polyhedron, but it is not a regular polyhedron. It is a truncated icosahedron, one of the semiregular polyhedra. Some of the faces are regular hexagons, and some are regular pentagons. Explain why not all of its faces can be regular hexagons. All the vertices have the same vertex type. What is it? How many pentagons are there and how many hexagons? How many vertices?
13. If you “unbulge” an ordinary soccer ball so that each of its sewn pieces is flat, you get a polyhedron, but it is not a regular polyhedron. It is a truncated icosahedron, one of the semiregular polyhedra. Some of the faces are regular hexagons, and some are regular pentagons. Explain why not all of its faces can be regular hexagons. All the vertices have the same vertex type. What is it? How many pentagons are there and how many hexagons? How many vertices?

13.
Three hexagonal faces meeting at at point would form a solid angle of , hence would form a flat surface. The vertex type on an ordinary soccer ball is 5.6.6. The ball has 32 faces (of which 12 are pentagons and 20 are hexagons), 60 vertices, and 92 edges.
Question 20.44
![]() 14. A soccer ball should be as round as possible, which suggests using many polygons, each of which is short across. Of course, making a ball with a large number of small pieces requires more sewing. A ball with 92 faces was used for some European soccer competitions: 12 pentagons, 20 hexagons, and 60 triangles (see the accompanying figure), all of them regular polygons. What are the possible vertex types for a polyhedron made up of pentagons, hexagons, and triangles? Explain why the polyhedron underlying this soccer ball is not semiregular.
14. A soccer ball should be as round as possible, which suggests using many polygons, each of which is short across. Of course, making a ball with a large number of small pieces requires more sewing. A ball with 92 faces was used for some European soccer competitions: 12 pentagons, 20 hexagons, and 60 triangles (see the accompanying figure), all of them regular polygons. What are the possible vertex types for a polyhedron made up of pentagons, hexagons, and triangles? Explain why the polyhedron underlying this soccer ball is not semiregular.

20.3 Using Only Translations

860
Refer to tiles (a) through (g) below in doing Exercises 15 and 16.
Question 20.45
15. For each tile (a) through (c), determine whether it can be used to tile the plane by translations. (From Frederick Barber et al., Tiling the Plane, COMAP, Lexington, MA, 1989, pp. p. 1 p. 8, 9.)
15.
(a) No
(b) No
(c) No
Question 20.46
16. Repeat Exercise 15, but for tiles (d) through (g).
Question 20.47
![]() 17. Start from a par-hexagon of your choice and modify it to tile the plane by translations. (You will probably find it useful to do your work on graph paper. If you choose a regular hexagon, special graph paper is available, ruled into regular hexagons, that would be particularly good to use.) Can you draw a design on the tile so as to make an Escher-like pattern?
17. Start from a par-hexagon of your choice and modify it to tile the plane by translations. (You will probably find it useful to do your work on graph paper. If you choose a regular hexagon, special graph paper is available, ruled into regular hexagons, that would be particularly good to use.) Can you draw a design on the tile so as to make an Escher-like pattern?
17.
Answers will vary.
Question 20.48
![]() 18. Start from a parallelogram of your choice and modify it to tile the plane by translations. (You will probably find it useful to do your work on graph paper.) Can you draw a design on the tile so as to make an Escher-like pattern?
18. Start from a parallelogram of your choice and modify it to tile the plane by translations. (You will probably find it useful to do your work on graph paper.) Can you draw a design on the tile so as to make an Escher-like pattern?
Refer to the following information in doing Exercises 19–22. A particularly simple kind of polygon, called a polyomino, is made of squares joined edge-to-edge. The name is a generalization of “domino”; indeed, there is only one kind of domino (two squares joined at an edge to form a rectangle). There are just two trominos (short for “triominos”), the straight tromino and the L-tromino. The straight tromino has the shape of a rectangle, so it can tile the plane by translations; the L-tromino has the shape of a hexagon.
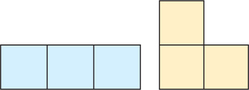
Question 20.49
19. Is the L-tromino convex? Does the result about which hexagons can tile the plane (on page 834) give any information about whether the L-tromino can tile the plane or not?
19.
No; no
Question 20.50
20. Find a tiling of the plane using just the L-tromino and translations of it. Is there more than one way to do the tiling?
Question 20.51
21. Show how alternative 2 of the Translation Criterion can be applied to the L-tromino.
21.
The only way to tile by translations is to fit the outer “elbow” of one tile into the inner “elbow” of another. Labeling the corners as follows works: the corners on the top and , those on the rightmost side and , the middle of the bottom , and the middle of the leftmost side .
A-42
Question 20.52
![]() 22. Explain why alternative 1 of the Translation Criterion cannot be applied to the L-tromino. (Hint: Label each of the eight corners of the component squares of the tromino with the letters . Let these be our candidates for the points , , , and of the criterion.) Each of the sides of the tromino that is 2 units long has nowhere to go under a translation. Any application of the criterion must divide each side into two pieces, so their midpoints must be two of the points , , , and . Make a similar argument about two corners of the tromino. Thus, we have four points, which can be labeled consecutively , , , and , starting at any one of them. Show that none of the four possibilities “works.” (This argument can be generalized to show that trying , , , and at points other than the corners of the squares won’t work either.)
22. Explain why alternative 1 of the Translation Criterion cannot be applied to the L-tromino. (Hint: Label each of the eight corners of the component squares of the tromino with the letters . Let these be our candidates for the points , , , and of the criterion.) Each of the sides of the tromino that is 2 units long has nowhere to go under a translation. Any application of the criterion must divide each side into two pieces, so their midpoints must be two of the points , , , and . Make a similar argument about two corners of the tromino. Thus, we have four points, which can be labeled consecutively , , , and , starting at any one of them. Show that none of the four possibilities “works.” (This argument can be generalized to show that trying , , , and at points other than the corners of the squares won’t work either.)
Question 20.53
23. Explain why there are no other tetrominos (each made of four squares joined at edges) than the five shown below—plus differing mirror images of two of them (which ones?). In the order shown, they are called the square, straight, T-, L-, and skew tetrominos.

23.
Answers will vary.
For Exercises 24–28, you will find it useful to make yourself several copies of each of the polyominos (e.g., by cutting them out of graph paper).
Question 20.54
24. Show how alternative 2 of the Translation Criterion applies to the T-tetromino.
Question 20.55
25. Apply alternative 1 of the Translation Criterion to the skew-tetromino and show how it can tile.
25.
Place the skew-tetromino on a coordinate system with unit length for the side of a square and with the lower left corner at (0, 0). Then and works.
Question 20.56
26. Show how alternative 2 of the Translation Criterion applies to the L-tetromino.
Question 20.57
27. Show how alternative 2 of the Translation Criterion can be applied to the skew-tetromino and show how it can tile.
27.
Place the skew-tetromino on a coordinate system with unit length for the side of a square and with the lower left corner at (0, 0). Then works.
Question 20.58
![]() 28. In Exercises 25 and 27, we indulged in what would appear to be “overkill,” demonstrating the same result in two different ways. Doing so can be useful in mathematics for giving greater understanding about why and how something occurs or is true. Here, those exercises should give you the idea that alternative 2 of the Translation Criterion can reduce to (and hence is more general than) alternative 1 if some points are allowed to coincide. For such a reduction, which pairs of points must coincide? (You are allowed to relabel the remaining four distinct points.)
28. In Exercises 25 and 27, we indulged in what would appear to be “overkill,” demonstrating the same result in two different ways. Doing so can be useful in mathematics for giving greater understanding about why and how something occurs or is true. Here, those exercises should give you the idea that alternative 2 of the Translation Criterion can reduce to (and hence is more general than) alternative 1 if some points are allowed to coincide. For such a reduction, which pairs of points must coincide? (You are allowed to relabel the remaining four distinct points.)
20.4 Using Translations Plus Half-Turns
Question 20.59
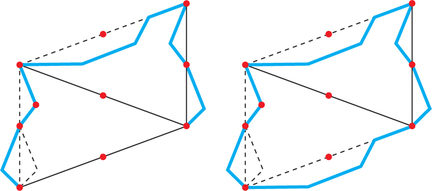
29. Explain how the final shape of Figure 20.18 on page 843 satisfies the Conway Criterion by identifying relevant points , , , , , and F.
29.
Answers will vary.
Question 20.60
30. Do the same as in Exercise 29, but for the final shape of Figure 20.19 on page 843.
For Exercises 31 and 32, refer to tiles (a) through (g) on page 859.
Question 20.61
31. For each tile (a) through (c), determine whether it can be used to tile the plane by translations and half-turns.
861
31.
(a) Yes
(b) No
(c) No
Question 20.62
32. Repeat Exercise 31 for tiles (d) through (g).
Question 20.63
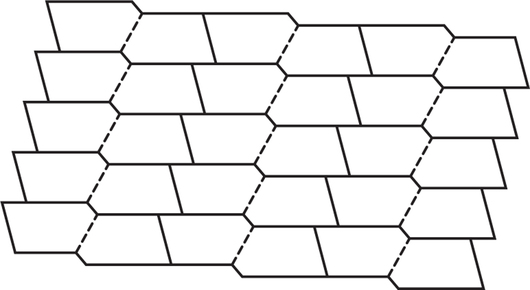
33. Show how an arbitrary pentagon with two parallel sides, such as the one shown below, can tile the plane.

33.
See figure below.
Question 20.64
34. The pentagon below is a pentagonal tile of type 13, which was discovered by Marjorie Rice. Show how it can tile the plane. (Hint: Carefully trace and cut out a dozen or so copies and try fitting them together.)
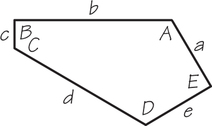
The parts of this pentagon satisfy the following relations:
[Adapted from Doris Schattschneider, “In Praise of Amateurs,” in David A. Klarner (ed.), The Mathematical Gardner, Wadsworth, Belmont, CA, 1981, p. 162.]
Question 20.65
35. Start from a triangle of your choice and modify it to tile the plane by translations and half-turns. (You will probably find it useful to do your work on graph paper.) Can you draw a design on the tile so as to make an Escher-like pattern of a plant, animal, or other object?
35.
Answers will vary.
Question 20.66
36. Start from a quadrilateral of your choice and modify it to tile the plane by translations and half-turns. (You will probably find it useful to do your work on graph paper.) Can you draw a design on the tile so as to make an Escher-like pattern of a plant, animal, or other object?
For Exercises 37–40, refer to the information about polyominos preceding Exercise 19. We saw earlier that all the dominos, trominos, and tetrominos tile the plane by translations. Here, we investigate the 12 pentominos, shown below with a letter notation for each. (If you allow mirror images to count as different pentominos, there are 18.) It will be useful for you to make several copies of each of them.
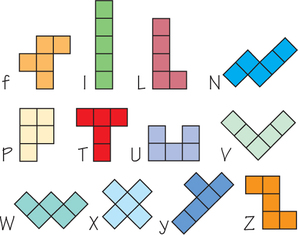
Question 20.67
37. By experimenting, determine which of the pentominos can tile the plane by translations. (Hint: There are nine.)
37.
N, Z, W, P, y, I, L, V, X. See www.srcf.ucam.org/~jsm28/tiling/5-omino-trans.ps.gz.
Question 20.68
38. Apply the Conway Criterion to the f-pentomino and show how it can tile by translations and halfturns.
Question 20.69
39. Apply the Conway Criterion to the U-pentomino and show how it can tile by translations and halfturns.
39.
Place the U on a coordinate system with unit length for the side of a square and with the lower left corner at (0, 0). Then works.
Question 20.70
40. Apply the Conway Criterion to the T-pentomino and show how it can tile by translations and half-turns.
Question 20.71
![]() 41. (Thanks to Doris Schattschneider, Moravian College.) In the text, we discuss some criteria and methods for generating Escher-like patterns that involve just translations or translations and half-turns. A slight variation on one such method allows construction of tilings that feature a tile and its mirror image. We modify a parallelogram so that two reflected tiles are joined and the joined pair tiles by translation. You get to design the shape of the tile and put whatever art you like on it.
41. (Thanks to Doris Schattschneider, Moravian College.) In the text, we discuss some criteria and methods for generating Escher-like patterns that involve just translations or translations and half-turns. A slight variation on one such method allows construction of tilings that feature a tile and its mirror image. We modify a parallelogram so that two reflected tiles are joined and the joined pair tiles by translation. You get to design the shape of the tile and put whatever art you like on it.
Begin with an isosceles triangle and mark the midpoint of each of its sides (it’s best to use graph paper or a dynamic geometry program). Half-turn the triangle about the midpoint of one of its two equal sides to produce a parallelogram.
Modify half of the (odd) third side in any manner—here is where you get to be creative!— joining a vertex to the midpoint of that side. Then reflect that modification in the side and translate it so that it joins the midpoint to the other vertex of that side.
862
Now translate the lower half of the modified side to the upper half of the opposite side of the parallelogram, and translate the upper half of the modified side to the lower half of the opposite side of the parallelogram.
Now modify one of the remaining sides of the parallelogram in any way you wish, and then translate that modification to the opposite side of the parallelogram.
Join a midpoint of the diagonal of the parallelogram to a midpoint of the side you have just modified (this line segment will be parallel to the other sides of the parallelogram). Reflect the side just modified in this segment, then translate the reflected modification so that it replaces the diagonal of the parallelogram. Your original parallelogram is now replaced by two tiles that are reflected images of each other. The outline of the joined pair of tiles is a modified par-hexagon that tiles by translations.
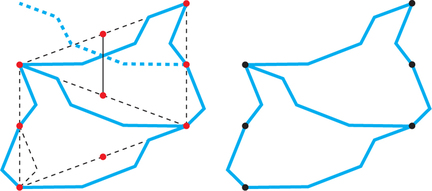
41.
Answers will vary.
Question 20.72
42. Does the Conway Criterion apply to the tilings created by the method of Exercise 41?
20.5 Nonperiodic Tilings
Question 20.73
43. (a) Describe the monohedral tilings of the line. (b)Describe the periodic tilings of the line that use two tiles of different lengths.
43.
(a) Consecutive segments, all of the same length; each length gives a different tiling.
(b) Let the lengths be and . Then the tilings are consecutive repetitions of any finite sequence of s and s.
Question 20.74
44. A line can be tiled quasiperiodically with a pair of tiles but only if their lengths are in the right proportion, so that the pattern can be scaled up. We determine what that proportion must be. Let the two lengths be (for “short”) and (for “long”), with and , where the scaling factor is . The key requirement for the scaling factor is that scaling up a tile of length produces a total length of , that is, .
- Using substitution, reduce the two equations and to a single equation, eliminating and leaving just and involved.
- Use the quadratic formula to solve for two possible values of . Since we want , we choose the larger value.
863
Exercises 45–48 illustrate the connection between nonperiodic tilings of the line and the Fibonacci numbers and golden ratio of Chapter 19 (but these exercises do not require any information from that chapter). (Thanks for this idea to David J. Wright, Oklahoma State University.) The rabbit problem in Chapter 19 (Exercise 4, page 814) leads us directly into quasiperiodic patterns (and even to musical sequences, as later exercises show). Let (for “adult”) denote an adult pair of rabbits and (for “baby”) denote a baby pair. We record the population at the end of each month, just before any births, in a systematic way, as a string of s and s. At the end of their second month of life, a rabbit pair will be considered to be adult and give birth to a baby pair.
At the end of the first month, the sequence is just , and the same is true at the end of the second month. When an adult pair has a baby pair , we write the new immediately to the right of the . So at the end of the third month, the sequence is ; at the end of the fourth, it is because the first baby pair is now adult; at the end of the fifth month, we have . (In this model, rabbits breed like clockwork, month after month, and never die!)
Question 20.75
45. What is the sequence at the end of the sixth month?
45.
Question 20.76
46. Explain why we can never have two s next to each other.
Question 20.77
47. Explain why we can never have three s in a row.
47.
The two leftmost As would have had to come from two s in a row in the preceding month.
Question 20.78
48. Show that from the fourth month on, the sequence for the current month consists of the sequence for last month followed by the sequence for two months ago.
For Exercises 49–51, we define inflation and deflation of a sequence of “tiles” consisting of s (“shorts”) and s (“longs”).
- Inflation: Replace each by and each by . For example, the inflation of ()()() would be , where we have inserted parentheses for clarity.
- Deflation: Replace each by and each lone by . For example, the deflation of ()()() would be , where we have inserted parentheses for clarity.
Question 20.79
49. (a) Start with just a single and repeat the inflation process, showing the stages, until you reach a stage with 21 tiles.
(b) How many tiles are there at each stage that you reached? (If you continue this process forever, you tile a half-line to the right; you could tile the entire line by reflecting this right half-line over to cover the left half-line. The result is called a Fibonacci tiling of the line because of the appearance of the Fibonacci sequence in the numbers of tiles.)
(c) If a line segment contains copies of the tile and copies of the tile, how many tiles will the inflation of the segment contain?
49.
(a)
(b) segments at stage
(c)
Question 20.80
50. (a) Apply deflation repeatedly to your answer to Exercise 49a, which has 21 letters, until you can deflate no further. What do you end up with?
(b) Apply deflation repeatedly instead to the periodic sequence …. What do you end up with?
(c) Devise your own periodic sequence of and tiles. Apply the deflation process to it repeatedly. What do you end up with? What do you conjecture?
![]() (d) Explain how the Fibonacci tiling is quasiperiodic.
(d) Explain how the Fibonacci tiling is quasiperiodic.
Question 20.81
![]() 51. Let a lone be considered the first stage of inflation. Show that at the nth stage of inflation, for , there are (the th Fibonacci number—see Section 19.1 on page 780) symbols in the sequence, of which are s and are s. (Hint: Check it for , and 4.)
51. Let a lone be considered the first stage of inflation. Show that at the nth stage of inflation, for , there are (the th Fibonacci number—see Section 19.1 on page 780) symbols in the sequence, of which are s and are s. (Hint: Check it for , and 4.)
51.
Let and be the number of Ls and the number of s at the th stage. Each at the th stage (for ) must have come from one in the previous stage, so . Similarly, we get an at the th stage from each and each in the previous stage, so . Using both these facts together, we have . We note that ,
. The sequence obeys the same recurrence rule as the Fibonacci sequence and starts with the same values one step later; in fact, it is always just one step behind the Fibonacci sequence: . Consequently, , and the total number of symbols is .
For Exercises 52–62, refer to the following. Call a sequence musical if repeatedly applying deflation to it eventually results in a single .
Question 20.82
52. Explain why inflation and deflation preserve musicality: If we inflate or deflate a musical sequence, we get another musical sequence. (Another way to think of this relationship is that a musical sequence is self-similar under inflation and deflation.)
Question 20.83
53. Explain why no musical sequence contains .
53.
In an inflated sequence, the only way an enters is as an preceded by an , so two Ss in a row cannot occur in a musical sequence.
Question 20.84
54. Explain why no musical sequence contains .
Question 20.85
55. Explain why no musical sequence ends in .
55.
If a sequence ends in , its deflation ends in , which Exercise 53 shows is impossible for a musical sequence.
Question 20.86
56. Explain why no musical sequence ends in .
Question 20.87
57. Show that apart from the lone sequence , every musical sequence is an initial subsequence of all the musical sequences that are successive inflations of it.
57.
It suffices to show that every musical sequence is an initial subsequence of its inflation. Note that for any musical sequence except , its inflation is longer; and for any except , its deflation is shorter. Let be the shortest musical sequence that is not an initial subsequence of its inflation . Now by hypothesis is not ; nor can be , because the inflation of is . Since is neither nor , it can be deflated and the deflation is shorter. Because is shorter than , is an initial subsequence of . But under inflation of to , the initial part of that is inflates to all of , followed by inflation of the rest of . Hence, is an initial subsequence of , contrary to the supposition that it isn’t.
Question 20.88
58. Exercises 53–56 give necessary conditions for a sequence to be musical. Are those conditions sufficient? That is, if a sequence does not contain or , and it does not end in or , must it be a musical sequence? (This is the kind of question that mathematicians ask in an effort to pin down the characteristics of a musical sequence.)
Question 20.89
59. We show how to check whether a finite block of s and s can be a part (subsequence) of some musical sequence or else is never a part of any musical sequence. We do so by deflating the block: If the deflation arrives at a single symbol, the block is part of a musical sequence; if the deflation cannot arrive at a single symbol, the block is not part of any musical sequence. However, we use a slightly modified form of deflation:
- If at any stage of the deflation of the block we arrive at as the starting symbol, we can tack on an initial in front of it (because as an internal part of a musical sequence, the deflated block would have to have an preceding the —it can’t have two Ss in a row and be musical).
- We add the rule that if at any stage of the deflation of the block we arrive at as the ending symbols, we replace the with (because as an internal part of a musical sequence, the deflated block would have to be followed by an —it can’t have three s in a row and be musical; at the next deflation, the would become .)
864
- If, at any stage of this modified deflation, we arrive at two or more s in a row or three or more s in a row, then the original block could not be part of a musical sequence. Otherwise, the original block will deflate eventually to a single symbol, at which point we conclude that the original block is a part of a musical sequence.
Check the two blocks below. Is either a part of a musical sequence?
59.
(a) Yes
(b) No
Question 20.90
![]() 60. (For students who have covered Chapter 19.) From Exercise 53, we know that each application of inflation to a musical sequence simply extends it. By successive inflation, then, we can build an infinite sequence. Argue that as we approach this limiting sequence, the ratio of s to s tends toward the golden ratio φ of page 780.
60. (For students who have covered Chapter 19.) From Exercise 53, we know that each application of inflation to a musical sequence simply extends it. By successive inflation, then, we can build an infinite sequence. Argue that as we approach this limiting sequence, the ratio of s to s tends toward the golden ratio φ of page 780.
Question 20.91
![]() 61. (For students who have covered Chapter 19.)
61. (For students who have covered Chapter 19.)
Conclude from Exercise 56 that the sequence cannot be periodic or settle into a periodic repetition after a finite “burn-in” period. Thus, the sequence is nonperiodic. (Hint: φ is not a rational number; that is, it cannot be represented as a ratio / of whole numbers and .)
61.
If the sequence were periodic, the limiting ratio of s to s would be the same as the ratio in the repeating part, which would be a rational number, contrary to the result of Exercise 56.
Question 20.92
62. (For students who have covered Chapter 19.) After applying deflation a large number of times, a large area of a Penrose pattern will contain some number kites and darts. At each deflation, a kite is broken down into two kites and two halves of darts, and a dart is broken down into a single kite and two halves of darts. Thus, each of the kites gives rise to 2 kites, and each of the darts gives rise to kites, for a total of new kites. Similarly, there will be new darts. The ratio of kites to darts will become
Assume that the ratio eventually stabilizes as the number of darts and kites gets larger and larger. What value does it tend to? Hint: Set and solve for .
Chapter Review
Question 20.93
63. Specify a formula for the measure of an exterior angle of a regular -gon.
63.
Question 20.94
64. Give a numerical reason why a semiregular tiling could not include both regular polygons with 12 sides and regular polygons with 8 sides (with or without any regular polygons with other numbers of sides).
Question 20.95
65. The Translation Criterion for tiling of the plane by translations alone offers two possibilities that guarantee such a tiling. State the details of one of these possibilities.
65.
See page 839.
Question 20.96
66. State the Conway Criterion in full detail: What kind of tilings does it refer to? What is the condition for such tiling?
Question 20.97
67. What is a quasicrystal? What is the connection of quasicrystals to Penrose tilings? What was so revolutionary about Penrose tilings?
67.
See Spotlight 20.6 (page 854).