8.4 8.3 Rules of Probability: Independent and Dependent Events
While everyday speech might make you think that the word independent could also be a synonym for words like disjoint and mutually exclusive, independent events have a different meaning in statistics. Independent events do not affect each other’s probability of occurrence, just as an individual’s probability of being chosen in a simple random sample (SRS) (see Section 7.3 on page 297) is not affected by whether another particular individual is selected.
Independent and Dependent Events DEFINITION
Two events are independent events if the occurrence of one event has no influence on the probability of the occurrence of the other event. If two events are not independent, then they are dependent events.
The diagram in Figure 8.12 depicts two independent events, and , represented by rectangular-shaped areas. In this diagram, since fills one-quarter of the area representing the sample space . Next, assume that has occurred—so the outcome lies inside ’s rectangle. Given this information, what is the likelihood that occurs? Notice that the purple area shows the outcomes in that are in . This overlap fills one-fourth of B’s rectangle. So the probability that occurs, given we know that has occurred, expressed as , is still 1/4. The information about did not influence how likely it was for to occur. Therefore, the two events are independent.
355
EXAMPLE 6 Dependent or Independent?
For many sweepstakes, the consumer is automatically entered into the drawing after making a purchase. However, often sweepstake rules state that “no purchase is required to enter,” and the consumer is given the option to enter by completing an online form or mailing in a postcard. Let event be winning the sweepstakes and event be making a purchase. According to the sweepstake rules, your chance of winning the contest is not affected by whether or not you make a purchase. If we use the notation as shorthand for “the probability of winning, given a purchase is made,” then according to the rules, . In this case, events and are independent.
For the next example, return to Figure 8.7 (page 347) in Example 3. Consider the following events:
Are events and independent or dependent? We know . But what about the probability that the sum on the dice is 7, given both dice show values less than 5—in other words, ? In Figure 8.13 the outcomes in event are outlined by a blue rectangle. Each outcome in , of which there are 16, is equally likely and there are only two outcomes in for which the sum of the dice is 7. Hence, . (The proportion of sums of 7 in the outcomes for differs from the proportion of sums of 7 in the sample space.) In this case, knowledge that event has occurred makes it less likely that occurs. Therefore, events and are dependent.
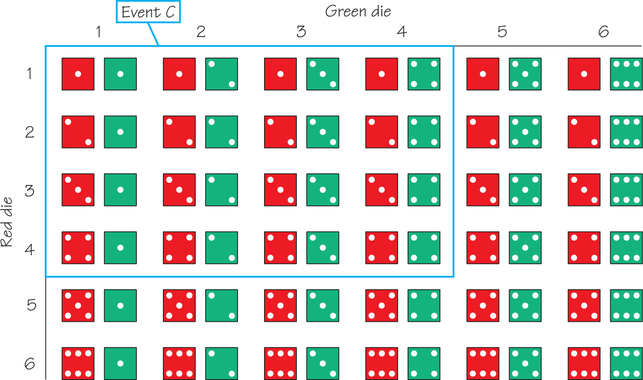
356
Self Check 4
Return to the context of rolling two dice and the events:
Are and independent? Support your answer.
. Next, we find . Event , shown in the blue rectangle, has six outcomes, each of which is equally likely. Given has occurred, there is only one way to get a sum of . . Therefore, and are independent.
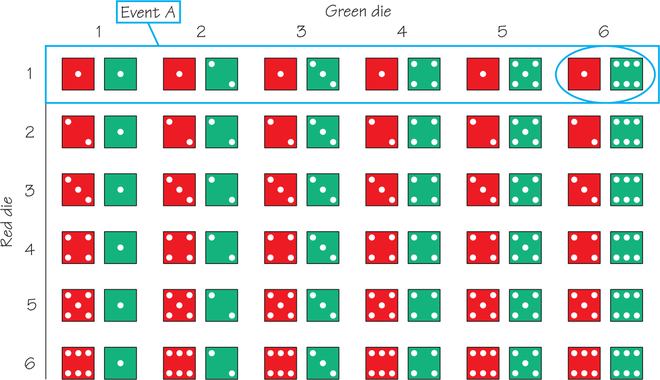
In Self Check 4, you should have found that events and were independent. (If not, check the Self Check answer at the end of this chapter.) Next, we learn how to find the probability that two independent events occur simultaneously. We begin with an example. Start with independent events and from Self Check 4. We want to determine . Rule 6, the multiplication rule for independent events, is the rule needed for calculating this probability.
- Rule 6. Multiplication Rule for Independent Events. If two events are independent, then the probability that one event and the other both occur is the product of their individual probabilities. In Self Check 4, you found that events and are independent. So we can find the probability that both and occur by multiplying the individual event probabilities:
To confirm this result, notice that the overlap of and is the simple event of rolling red = 1 and green = 6, which has probability .
EXAMPLE 7 Probabilities for Driving to Work
In the discussion of Rule 4 (the addition rule for disjoint events, page 351), we determined that 86% of workers drive to work (either alone or in a carpool). Suppose a random sample of two U.S. workers is chosen. What is the probability that they both drive to work? To answer this question, let:
We want . Since the workers were chosen randomly, events and are independent. Therefore, we use the multiplication rule for independent events to determine this probability:
Hence, the likelihood that both workers drive to work is approximately 74%.
Next, we turn our attention to dependent events. We know from Example 6 that the events of rolling a sum of 7 (event ) and having both dice show a number less than 5 (event ) are dependent events. Knowing that has occurred influences the probability that occurs. The result, is called a conditional probability.
357
Conditional Probability DEFINITION
The conditional probability of given , written as , can be computed by dividing the probability that both events occur by the probability that occurs:
In cases where and are independent, we can apply the multiplication rule for independent events:
Notice, that in order to calculate , we need .
Solving for in the formula for calculating a conditional probability allows us to generalize the multiplication rule so that it applies to situations where the two events are dependent. This leads to Rule 7.
Algebra Review Appendix
Solving for One Variable in Terms of Another
- Rule 7. General Multiplication Rule. Given two events and with , the probability that both occur is the conditional probability that occurs given has occurred times the probability that occurs. Take, for example, the situation in Figure 8.14. We want . The outcome “ and ” is represented by the overlap of and (purple area). It is easy to see that because ’s area overlaps half of ’s area. In addition, because ’s area covers one quarter of the area in the large rectangle representing the sample space . Applying the general multiplication rule we get . To confirm this result, notice that the area for “ and ” (purple area) does, in fact, cover one-eighth of the area in the large rectangle representing .
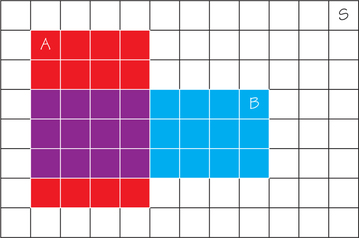Figure 8.14: Figure 8.14 Two dependent events.
As we did for Rules 1 through 5, we now state Rules 6 and 7 more concisely using more formal mathematical notation.
358
Probability Rules RULE
- Rule 6. The multiplication rule for independent events: .
- Rule 7. The general multiplication rule: provided .
EXAMPLE 8 Arsenic Testing: Using the General Multiplication Rule
Tests, whether medical screening tests for diseases or testing drinking water for health- risk contaminants, are not perfect. Take, for example, testing for arsenic in drinking water. Suppose that a test for arsenic in the water supply correctly reports the presence of arsenic (positive test result) with probability 0.97, and correctly reports the absence of arsenic (negative test result) with probability 0.86. Only about 4% of the drinking water in the United States is thought to contain arsenic.
Using the information above, we want to determine the following two probabilities:
- The probability that a randomly chosen water sample actually contains arsenic and yields a positive test result.
- The probability that a randomly chosen water sample does not contain arsenic and yields a negative test result.
Next, we translate what we know and what we want to find into mathematical notation. Let be the event that a water sample contains arsenic, and let be the event that the sample does not contain arsenic. Let “+“ represent the event that the test results come back positive for arsenic, and “−” the event that the test results come back negative.
- What we know: , and
- What we want to find: and
Using the information from the first bullet and the general multiplication rule, we calculate probabilities 1 and 2 as follows:
Conditional probabilities also follow Rules 1 through 5 given in Section 8.2. In the next example, we use the complement rule (Rule 3) to find another set of probabilities associated with testing for arsenic in drinking water.
EXAMPLE 9 Arsenic Testing: Conditional Probability Models
Using the information on testing for arsenic given in Example 8, we construct a model for the conditional probability of possible test results given the water contains arsenic.
From information about the test, we know that . Using the complement rule (Rule 3) gives the probability of a false negative:
Fortunately, this probability is quite low! Table 8.4 gives the model for the conditional probability of the test results given the water sample contains arsenic.
| Outcome | Positive test | Negative test |
| Conditional probability given arsenic | 0.97 | 0.03 |
359
Self Check 5
When the water sample does not contain arsenic, there are two possible outcomes for the test results: positive (in this case, a false positive) and negative. Make a table similar to Table 8.4 that gives the conditional probability model of the test results given the water sample does not contain arsenic.
Outcome Positive test Negative test Conditional probability given no arsenic 0.86
In Examples 8 and 9, we have used probability rules to find a number of probabilities associated with testing water samples for arsenic. Now, suppose your water is the one randomly chosen for testing and the test comes back positive. How worried should you be that your water is contaminated by arsenic? Your level of worry should be connected to the probability that the water sample contains arsenic given the test comes back positive, . We find this probability in Example 10.
EXAMPLE 10 Arsenic Testing: How Worried Should You be about a Positive Test Result?
We begin with a tree diagram, shown in Figure 8.15, to identify the sample space of all possible outcomes, and use the general multiplication rule (Rule 7) to assign probabilities to each outcome in the sample space. Two of these probabilities were already computed in Example 8. In addition, the tree diagram contains the conditional probability models from Example 9 and Self Check 5.
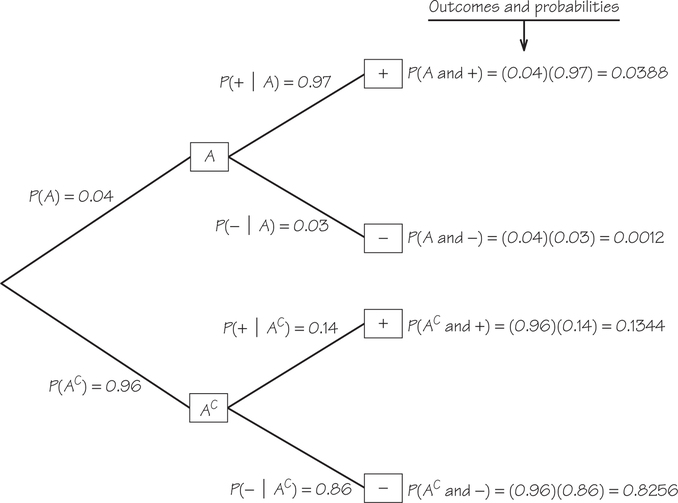
360
We want , which by the definition of conditional probability we calculate as follows:
From the tree diagram, we know . Next, we need . There are two ways to get a positive result: or . Since these are disjoint events, we use the addition rule for disjoint events (Rule 4) to find :
Next, we substitute and into the conditional probability formula:
In this situation, only around 22% of the water samples that test positive for arsenic actually contain arsenic. So, until further testing is done, you probably shouldn’t be in total panic mode. In Self Check 6, you will see how this probability changes when the likelihood of having arsenic in the water supply is increased.
Self Check 6
Suppose that, due to an environmental spill in a particular region, the probability of arsenic in the water supply is thought to be 0.5. What is the probability that a randomly chosen water sample (from this region) that tests positive for arsenic actually contains arsenic? If that water sample happens to be from the water that you drink, should you be worried?
Should be worried; the chance that arsenic is in the water, given the test was positive, is high.
Bayes Rule Applied to Testing for a Characteristic RULE
The mathematics involved in Example 10 on testing for some characteristic can be summarized as follows. and are called the prior probabilities. Given the prior probabilities and the conditional probabilities, and , we can determine what are called the posterior probabilities, and , using the following formulas: