4 Arbitrage and Spot Exchange Rates
Amen! Arbitrage is also one of the fundamental concepts of modern finance.
Arbitrage is the strategy of exploiting profit opportunities caused by price differences: buy low and sell high. If profits are zero then the market is in equilibrium and satisfies a no-arbitrage condition.
1. Arbitrage with Two Currencies
The simplest example: Consider the spot rate between the dollar and the euro in New York and London. Argue that if 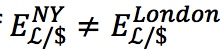 then profits can be made; exploiting them will cause rates to adjust until the no-arbitrage condition
then profits can be made; exploiting them will cause rates to adjust until the no-arbitrage condition  is achieved.
is achieved.
2. Arbitrage with Three Currencies
Now add the euro, so that there are three currencies in one place: New York. Explain how triangular arbitrage drives the three rates satisfy the no-arbitrage condition E£/$ = E£/€/E$/€. The left-hand side of this equation is called the direct exchange rate; the right-hand side is called the cross-rate.
3. Cross Rates and Vehicle Currencies
Cross rates are important because the vast majority of currencies are not traded directly with each other, but rather are traded indirectly via vehicle currencies such as the dollar, the euro, pound, or the yen. This reduces transactions costs.
The most basic of activities pursued by private actors in any market is arbitrage, a trading strategy that exploits any profit opportunities arising from price differences. Understanding arbitrage is one of the keys to thinking like an economist in any situation and is essential in studying exchange rates.
In the simplest terms, arbitrage means to buy low and sell high for a profit. If such profit opportunities exist in a market, then it is considered to be out of equilibrium. If no such profit opportunities exist, there will be no arbitrage; the market is in equilibrium and satisfies a no-arbitrage condition.
44
Arbitrage with Two Currencies
In teaching about arbitrage, always proceed in two steps: First, ask "given current prices, how can I make a profit?" Second, ask "If everybody else acted in the same way what would happen to prices?"
Suppose you trade dollars and pounds for a bank with branches in New York and London. You can electronically transfer the funds cost free between the two branch locations. Forex trading commissions are the same in each city and so small as to be negligible. Suppose the exchange rate in New York is 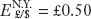 per dollar, in London
per dollar, in London 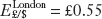 per dollar. Can you make a profit for the bank?
per dollar. Can you make a profit for the bank?
Yes. You can buy $1 for £0.50 in New York and sell it for £0.55 in London for an instant, riskless profit. Indeed, everyone would buy in New York and sell in London.
In general, one of the three outcomes can occur in the forex market. The spot rate can be higher in London: 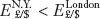 ; the spot rate can be higher in New York:
; the spot rate can be higher in New York: 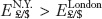 ; or the spot rate can be the same in both locations:
; or the spot rate can be the same in both locations: 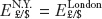 . Arbitrage occurs in the first two cases. Only in the last case, in which spot rates are equal, does no arbitrage occur. Hence, the no-arbitrage condition for spot rates is
. Arbitrage occurs in the first two cases. Only in the last case, in which spot rates are equal, does no arbitrage occur. Hence, the no-arbitrage condition for spot rates is

Figure 13-6 shows the no-arbitrage condition. Following both sets of arrows (AB and ACDB), we see that on each path we start with a dollar and end up with pounds, but we are indifferent between these paths only when the end result is identical. This situation would be an equilibrium, in which no arbitrage is possible.
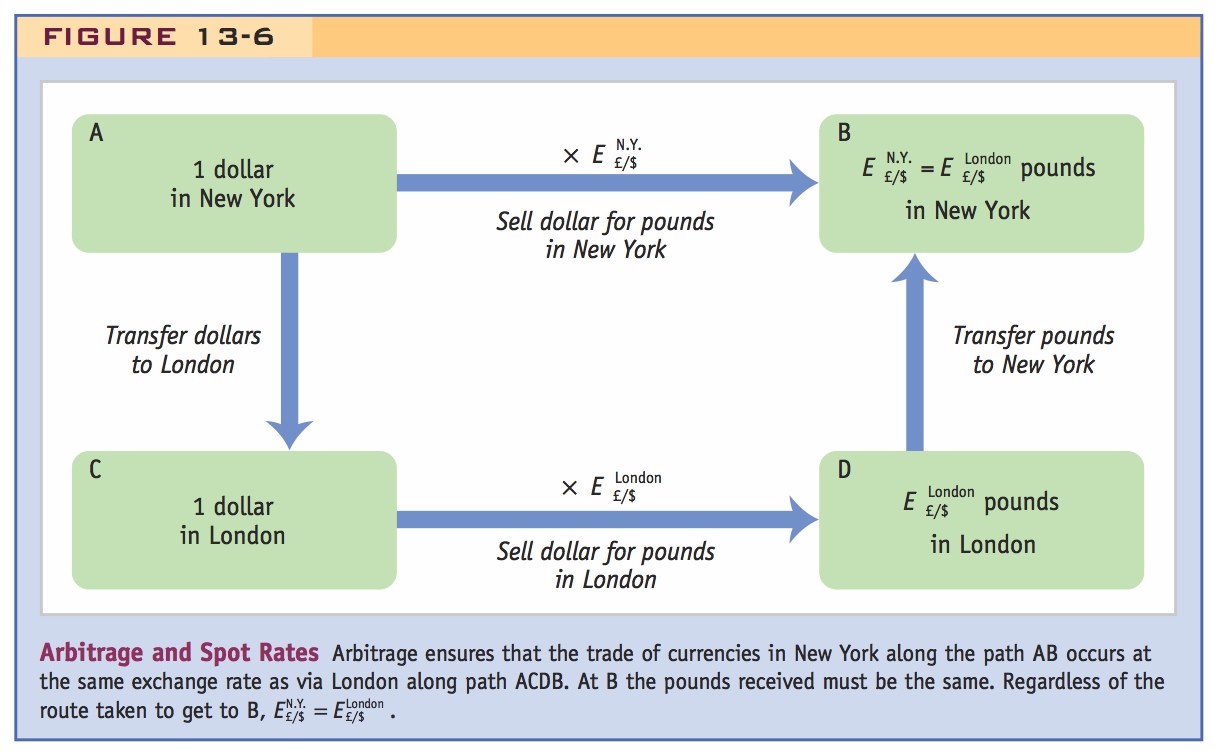
If the market is out of equilibrium, arbitrage would drive up the price in the low-price market and drive down the price in the high-price market. In our example, everyone buying dollars in New York and selling them in London would bid up the spot rate in New York from £0.50 and would bid down the spot rate in London from £0.55. This process would continue until the prices converged, arbitrage ceased, and equilibrium was reached. In forex markets, these adjustments happen nearly instantaneously, whether in the high-tech electronics markets of world financial centers or in the markets on street corners in the developing world.
45
Arbitrage with Three Currencies

AP Photo/Aijaz Rahi
Working through triangular arbitrage is tedious. However, it is still a useful exercise, for two reasons: (1) It forces students to apply arbitrage reasoning in a slightly more complicated setting. (2) It sets the stage for vehicle currencies.
The same logic that we just applied to transactions between two currencies can also be applied to transactions involving three currencies. Again, as the trader in New York, you are considering trading dollars and pounds, but you also consider indirect or “triangular” trade via a third currency, say, the euro. Triangular arbitrage works as follows: you sell dollars in exchange for euros, then immediately sell the same euros in exchange for pounds. This roundabout way to acquire pounds is feasible, but is it sensible? Perhaps.
For example, suppose euros can be obtained at E€/$ = €0.8 per dollar, and pounds can be obtained at E£/€ = £0.7 per euro. Starting with $1, you can obtain 0.8 euros, and with those 0.8 euros, you can obtain 0.7 × 0.8 pounds. Thus, setting aside the negligibly small commissions, the resulting pound–dollar exchange rate on the combined trade is E£/€ × E€/$ = 0.7 × 0.8 = 0.56 pounds per dollar. If, say, the exchange rate on the direct trade from dollars to pounds is a less favorable E£/$ = 0.5, we can trade $1 for £0.56 via the euro, and then trade the £0.56 for $1.12 by way of a direct trade (because 1.12 = 0.56/0.5), a riskless profit of 12 cents.
In general, three outcomes are again possible. The direct trade from dollars to pounds has a better rate: E£/$ > E£/€E€/$; the indirect trade has a better rate: E£/$ < E£/€E€/$; or the two trades have the same rate and yield the same result: E£/$ = E£/€E€/$. Only in the last case are there no profit opportunities. This no-arbitrage condition can be written in two ways:
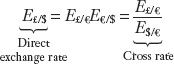
The right-hand expression, a ratio of two exchange rates, is called a cross rate. Examine the units carefully and notice how the two € cancel out. This no-arbitrage condition applies to all currency combinations and is illustrated by the paths AB and ACB in Figure 13-7 (you can see why it is called triangular arbitrage).
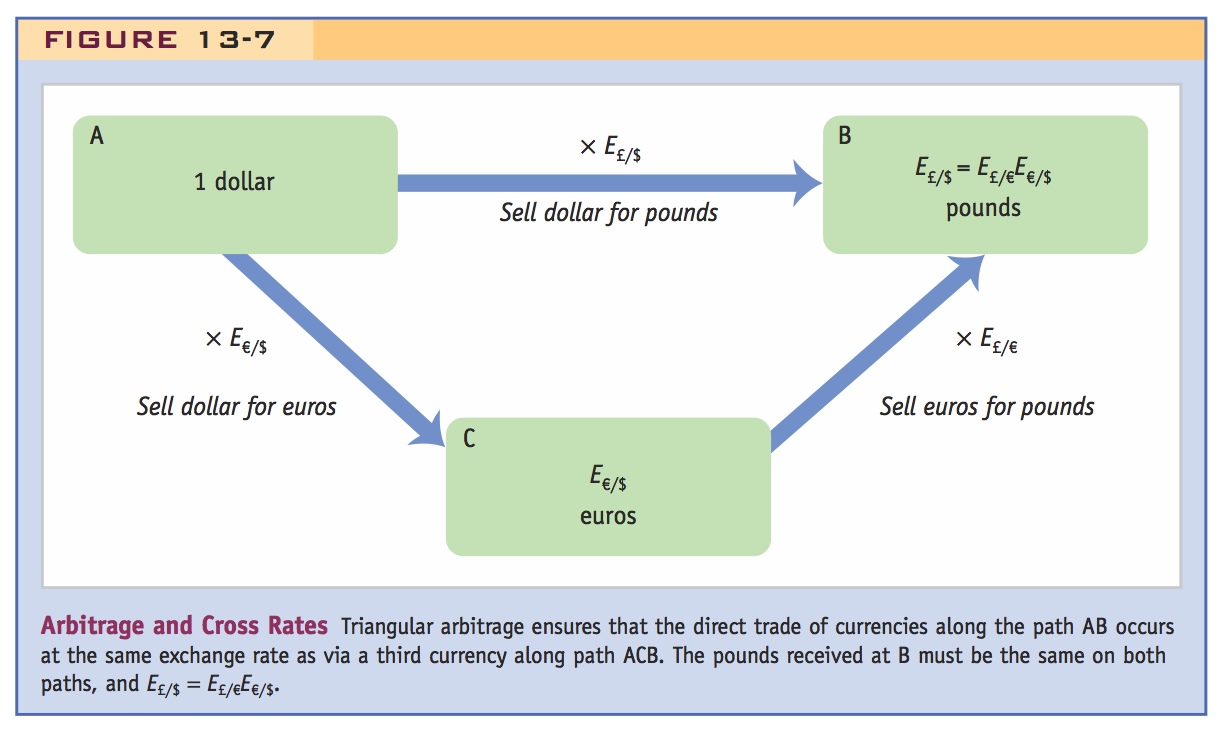
The cross rate formula is very convenient. It means that we do not need to keep track of the exchange rate of every currency at all times. For example, if we know the exchange rates against, say, the dollar, for every currency, then for any pair of currencies A and B we can use the dollar rates of each currency and the cross rate formula to work out the rate at which the two currencies will trade: EA/B = EA/$/EB/$. In practice, this is how most exchange rates are calculated.
46
Cross Rates and Vehicle Currencies
The benefits of vehicle curencies.
The study of cross rates is not a meaningless exercise because the vast majority of currency pairs are exchanged for each other through a third currency. There are 164 distinct currencies in the world at the time of this writing. If you write down every possible currency pair, then count them up, there would be 13,366 active forex markets in operation. In reality, however, there are only a tiny fraction of this number. Why?
The vast majority of the world’s currencies trade directly with only one or two of the major currencies, such as the dollar, euro, yen, or pound, and perhaps a few other currencies from neighboring countries. This is not too surprising. After all, to take some obscure examples, how often does somebody want to trade a Kenyan shilling for a Paraguayan guaraní? Or a Mauritanian ouguiya for a Tongan pa’anga? These are small, far-apart countries between which there is very little international trade or investment. It is hard to find counterparties for forex trade in these currencies—so hard that the costs of trading become prohibitive. And there is no need to bear these costs because, to continue our example, Kenya, Paraguay, Mauritania, and Tonga conduct a lot of business in major currencies such as the U.S. dollar, so individuals always have the option to engage in a triangular trade at the cross rate to convert shillings to dollars to guaranís (or ouguiyas to dollars to pa’angas), all for a reasonable commission.
Invite discussion of whether this might change.
When a third currency, such as the U.S. dollar, is used in these transactions, it is called a vehicle currency because it is not the home currency of either of the parties involved in the trade. Market data illustrate the importance of vehicle currencies. According to the 2010 survey data from the Bank for International Settlements, the most common vehicle currency is the U.S. dollar, which appears on one side of 85% of all global trades. The euro is next, playing a role in 39% of all trades (many of them with the U.S. dollar). The yen appears in 19% of all trades and the British pound in 13%.
47