1 Exchange Rates in the Long Run: Deviations from Purchasing Power Parity
Deviations from PPP have important implications for policy and exchange rate deviation. This section develops a theory of deviations from PPP by introducing trading costs.
1. Limits to Arbitrage
Assume proportional trading costs of c. Recall that the real exchange rate is q = EP*⁄P. Then arbitrage will only be profitable if 1⁄(1 + c) > q > 1 + c. Consider three cases (1) Zero costs, c = 0, where q = 1 and LOOP holds. (2) Low costs, where small deviations from LOOP are possible, but LOOP holds approximately. (3) High costs, where LOOP does not hold. The larger the trading costs, the larger are the possible deviations from LOOP. If LOOP fails for enough goods, PPP will fail.
a. Trade Costs in Practice
Types of trade costs include transportation costs and tariffs and quotas. They are large, particularly for developing countries.
According to the most recent data from the World Bank, in 2012 gross national income per capita in the United States was $50,120, but by converting incomes using the exchange rate, it was found that gross national income per capita in China was only $5,740, about 11.5% of the U.S. level. Were the Chinese really that poor in terms of material living standards? No.
Show exactly how to do these calculations, using general Ps, Ys, and, reminding them of the definition of q.
When the calculations were repeated by comparing dollar incomes with the dollar prices of baskets of consumer goods, Chinese gross national income per capita was found to be about $9,210 in terms of U.S. consumer goods, so that nation’s living standards were now seen to be almost twice as high, at 18.4% of the U.S. level. The reason: in dollar terms, most goods cost a lot less in China than in the United States. The dollar price level in China was lower than in the United States. The implication: purchasing power parity (PPP) does not hold, and the real exchange rate is a long way from 1.
Emphasize how important it is to compare incomes adjusting for PPP. Perhaps have them look at the World Penn Tables https://pwt.sas.upenn.edu/.
These adjustments have many implications: for example, they affect calculations of living standards, poverty, allocations of aid, and projections of growth, consumption, demographics, pollution, and so on. So we need to understand these deviations from PPP for many reasons, including the need to refine our theory of exchange rates. When we learned about long-run exchange rates, we showed that we could predict the expected future exchange rate using the monetary approach to exchange rates, if purchasing power parity holds, that is, if baskets of goods sell for the same price in all locations. This theory provided a workable model of real exchange rates, but it was far from perfect. In this section, we address a major deficiency in PPP theory: its assumption that all goods are costlessly tradable.
Limits to Arbitrage
One way to set up a more realistic economic model would be to introduce costs of trading, which is now an important area of research in international economics.
To gain familiarity with trade costs and to see how they matter, let’s assume that the cost of trading the good equals some fraction c of the unit cost of the good at its source. For example, suppose there is one good, and it sells for P = $100 in Home. It costs $10 to ship the good from Home to another country, Foreign. The trade cost is c = 0.1 = 10%. The cost of the good on arrival in Foreign, including the trade cost, would be P × (1 + c) = $110.
451
Students will ask what sorts of things constitute trade costs. The text addresses this a bit later, but be prepared to provide a tentative answer now.
How do trade costs affect arbitrage? If you were considering trying to make an arbitrage profit by shipping a $100 widget from Home to Foreign, then you wouldn’t even think of doing it unless the Foreign price converted into dollars EP* was at least $110 (where E is Home’s exchange rate, and P* is the Foreign price in Foreign currency). Otherwise, you make a loss once the trading costs are taken into account. Similarly, going from Foreign to Home, you wouldn’t ship goods unless the Home price P was at least 10% above the foreign price EP*.
Formally, the ratio of the prices in the two locations can be written in proportional terms as q = EP*/P. As we learned in our study of long-run exchange rates, for any basket of goods, q is also known as the real exchange rate of the home country. Thus, if P = $100 and EP* = $110, then this relative price ratio would be (110/100) = 1.1.
Motivate this argument, as the text does, by asking the students how they could try to make profits by commodity arbitrage.
As we have just seen, arbitrage from Home to Foreign is profitable only if the Foreign price is higher than the Home price adjusted for the trade cost, which requires q = EP*/P > 1 + c. Conversely, arbitrage the other way is profitable only if the Home price is sufficiently higher than the Foreign price, with 1/q = P/(EP*) > 1 + c.
Thus, if q is below 1 + c, there will be no arbitrage from Home to Foreign. And if q is above 1/(1 + c), there will be no arbitrage from Foreign to Home. So we have shown that, taking trade costs into account, the no arbitrage condition for market equilibrium is
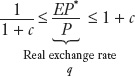
Let’s look at what this condition implies for various levels of trading costs.
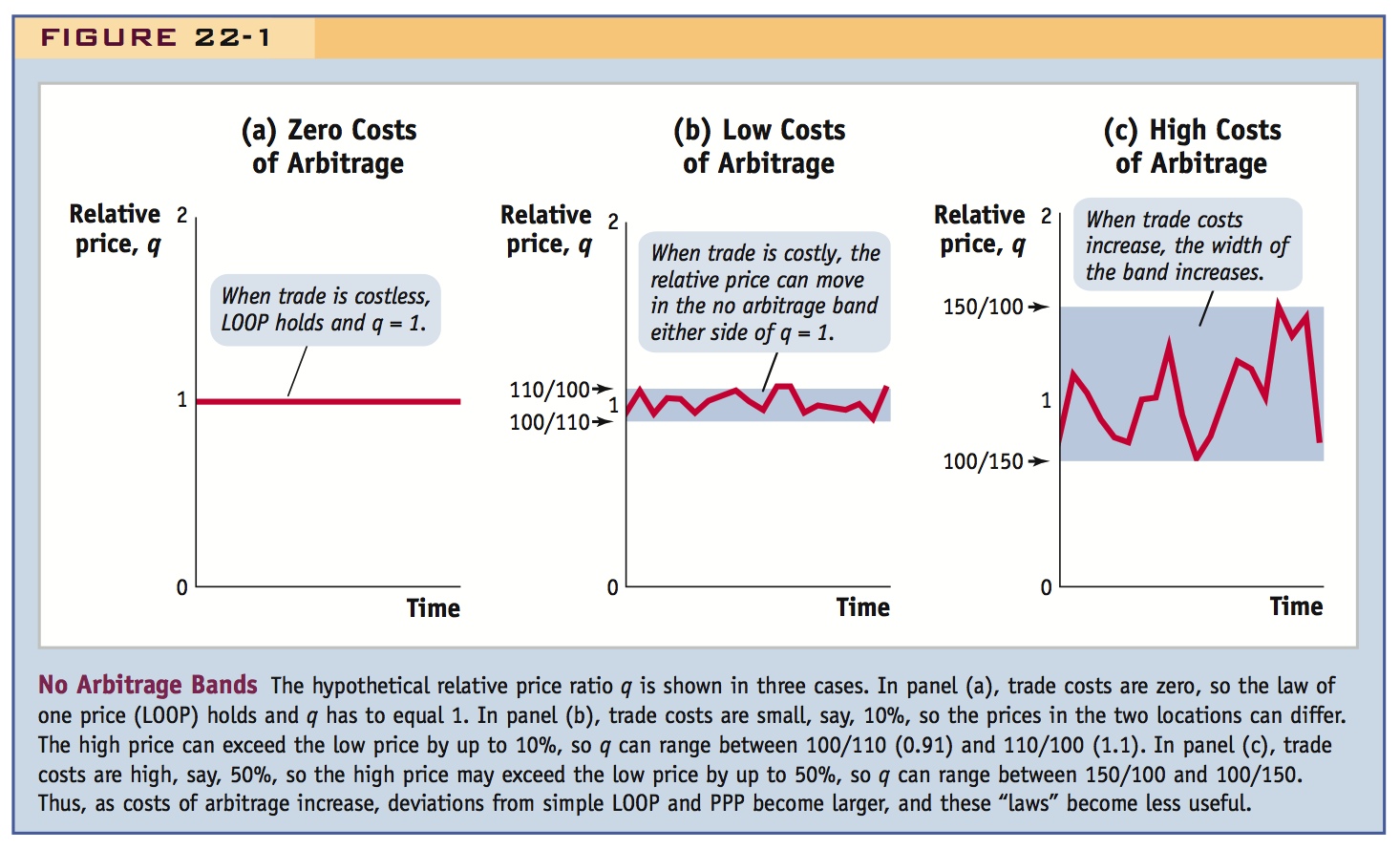
- Zero costs. With c = 0, the no arbitrage equilibrium condition reduces to an equality because both left- and right-hand sides equal 1, implying that q = 1. This equality is the condition for the law of one price (LOOP), which we expect to hold when arbitrage is costless. An illustration is shown in Figure 22-1, panel (a), which plots the hypothetical relative price q over time for Home and Foreign.
- Low costs. Suppose c is low, say, 10%, as in our example. If the price difference between source and destination is less than 10%, then there is no arbitrage. Hence, q is free to wander in what is called a no-arbitrage band between 1/(1 + c) = (100/110) and 1 + c = (110/100). For values of q between 0.91 and 1.1, then, the market is considered to be in equilibrium. This is shown in Figure 22-1, panel (b). Small deviations from LOOP are possible, but LOOP is still approximately true.
- High costs. Suppose c is high, say, 50%. If the price difference is less than 50%, there will be no arbitrage. There is a wider no-arbitrage band between 1/(1 + c) = (100/150) and 1 + c = (150/100) in which the market is in equilibrium and no arbitrage is possible. This is shown in Figure 22-1, panel (c). Deviations from LOOP are possible in the range 0.67 to 1.5, and LOOP no longer applies.
This may remind students of the gold points in the discussion of the gold standard.
Summarize these arguments with Table 22-1, which should be pretty intuitive.
This analysis shows that when trade costs or costs of arbitrage are higher, arbitrage will not happen for small price deviations, and the possible deviations from LOOP become greater. If the prices of many goods deviated from LOOP, this would imply deviations from PPP. If costs are huge, then arbitrage is practically impossible and the prices of the same good in two locations need not bear any relation to one another and can be very far apart. Under such conditions, goods are almost always nontraded, and LOOP and PPP will not apply.
452
Trade Costs in Practice These results show that when evaluating LOOP for one good or PPP for a basket of goods, we must take into account trade costs and consider how they affect deviations from price equality. Empirical research suggests that trade costs are affected by economic policies, as well as by characteristics of goods and their markets.1
Emphasize how much trade costs vary across goods, but also how large they are on average.
An important part of trade costs is costs of transportation. For U.S. imports, for example, estimated freight rates vary from 1% of the good’s price (for transport equipment) to 27% (for fertilizer). In many countries with worse transport infrastructure, these costs can be much higher: one estimate suggests that the average landlocked country has transport costs 55% higher than the average coastal country.
453
Another major factor that influences trade costs is a country’s trade policy. Average tariffs of 5% (rich countries) or more than 10% (developing countries) constitute an additional cost, and such tariffs vary widely by type of good. Quotas (limits to import quantities) and regulatory barriers (such as health and environmental regulations) also add to trade costs, but the costs they add are difficult to compute. In addition to transport and policy costs, economists have found statistical evidence of other causes of price gaps between markets, including distance between markets, crossing international borders, having different currencies, having floating exchange rates, and so on.
The illustration that follows shows the magnitudes of international trade costs for advanced countries.2 Like the variable c above, these costs are expressed as a percentage markup over the pre-shipment price of the goods. The data are averaged over all types of goods and based on direct measurements and econometric estimates:3

(Note that the subcosts are aggregated by compounding: e.g., a 21% markup on top of a 44% markup on a $1 good in the middle column results in a 74% markup in the left column, because 1.21 × 1.44 × $1 = $1.74.)
Also emphasize that trade costs are larger for less developed countries.
These data show that trade costs are large—and typically, they are even larger outside the advanced countries and create a very wide no-arbitrage band. This observation has led economists to incorporate trade costs into our economic models, so we can develop a more realistic theory of what goes on in the real world.
The Economist’s Big Mac Index finds wide variation in the dollar cost of Big Mac’s worldwide; similarly for prices of a Starbuck’s tall latte. Rich countries have higher price levels. Costs of nontraded goods, like local labor, might explain this. Why?
2. Nontraded Goods and the Balassa-Samuelson Model
Take an extreme case with two goods, one traded and one nontraded (infinite trading costs).
a. A Simple Model
Assumptions: (1) The price of the traded good is determined in the world market and is exogenous. (2) Productivity in traded goods determines wages: The wage in each country is equal to the MPL in its traded-goods sector. For simplicity, assume that the MPLs are constant and equal to A and A* at home and abroad. (3) Wages in turn determine the prices of nontraded goods. Higher wages imply higher marginal costs of production. Conclusion: Countries with more productive traded-good sectors, will have higher wages, higher costs, and so higher prices of nontraded goods. They will therefore have higher price levels, since the price of traded goods is fixed.
b. Changes in Productivity
If a country enjoys productivity growth, its wages will increase, raising costs, so its price level will increase. In fact, if the growth rate of domestic productivity is ΔA/A then its price level increases by ΔP/P = ηΔA/A, where η is the share of nontraded goods. A similar result applies to the other country, so that real depreciation is Δq⁄q = η((ΔA*)⁄(A* - ΔA⁄A)
c. Generalizing
An increase in a country’s productivity should raise prices and cause a real appreciation.
3. Overvaluations, Undervaluations, and Productivity Growth:
Forecasting Implications for Real and Nominal Exchange Rates
Empirically, price levels are higher in rich countries, so that q ≠ 1 even in the long runs. If in the short run the actual q is greater than (less than) the value of 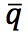 predicted by Balassa-Samuelson we say the real exchange rate is undervalued (overvalued).
predicted by Balassa-Samuelson we say the real exchange rate is undervalued (overvalued).
a. Forecasting the Real Exchange Rate
Forecasting q has two steps:
b. Convergence
Given the deviation of q from 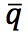 determine its speed of convergence to
determine its speed of convergence to  . This is normally at about 2 percent per year.
. This is normally at about 2 percent per year.
c. Trend
Determine the trend growth of 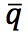 by looking at the growth rates of GDP and using the formula.
by looking at the growth rates of GDP and using the formula.
d. Convergence + Trend
Put b and c together.
e. Forecasting the Nominal Exchange Rate
By definition E = q P⁄P*). Therefore ΔE⁄E = Δq⁄q + ΔP⁄P - ΔP*)⁄P*. This generalizes the results of the monetary model with PPP, where it was sufficient to look at the inflation differential.
f. Adjustment to Equilibrium
Balassa-Samuelson does not tell us how q will adjust. If there is an undervaluation (overvaluation) convergence may either be (1) domestic prices increasing faster (slower) than abroad, or (2) a nominal depreciation (appreciation), or some combination of the two.
The Big Mac Index is always fun, so have them find the most recent article and talk about it in class. Then highlight these systematic deviations from PPP, since it will motivate nontraded goods and Balassa-Samuelson.
It’s Not Just the Burgers That Are Cheap
If real exchange rates can deviate from the PPP-implied value of 1, the next question to ask is, how do they vary, and why? One place to find a clue is in the pattern of deviations from PPP. For example, look at the Economist newspaper’s Big Mac index by searching the Internet for “economist big mac index.” If deviations from PPP were random, they might easily be dismissed as an approximation error. However, deviations from PPP in the Big Mac index are not entirely random: burgers tend to be cheaper in poorer countries. In July 2012, for example, the Economist found that, expressed in U.S. dollars, a Big Mac cost 38% less in Mexico and 46% less in Malaysia than it did in the United States.
454
It isn’t too difficult to think of a reason for this finding—the presence of nontraded goods. A Big Mac is a combination of some traded goods (such as flour, beef, and special sauce) and some nontraded goods (such as cooks and cleaners). Local labor wages are a large percentage of the costs of nontraded goods, so such goods tend to cost less in a poor country where wages are lower. The evidence in Figure 22-2, panel (a), supports this logic. This scatterplot shows that the dollar price of the Big Mac is strongly correlated with the local hourly wage in dollars.
Why stop here? The argument shouldn’t apply only to burgers, and indeed in 2004 the Economist did a parallel experiment and compared the prices of another globally uniform and omnipresent consumer product: the Starbucks tall latte. Similar patterns emerged: in dollar terms (adjusting for international variations in the size of the cups) the latte cost 15% less in Mexico and 25% less in Malaysia than it did in the United States.

The argument applies to most goods that are included in calculations of national price levels. Almost all goods have some local, nontraded component—some local value added or some local retail and distribution costs. Thus, the general price level should vary systematically in the same way, and it does. Figure 22-2, panel (b), shows that a country’s price level is strongly correlated with the level of GDP per person. Rich countries have higher price levels; their baskets cost more. In other words, the real exchange rate q = EP*/P does not equal 1 for all countries, and PPP does not hold, even in the long run. The remainder of this section explores this pattern using economic theory and considers what effect the lack of PPP has on the exchange rate models and predictions we developed earlier in the book.
There is now also an iPad index.
Emphasize the takeaways: (1) the importance of nontraded goods; (2) the fact that richer countries have higher price levels.
455
Nontraded Goods and the Balassa-Samuelson Model
Trade costs have major implications for international macroeconomics. In fact, by expanding our analysis from one good that is traded to two goods—one traded and one not traded—we can explain price level differences and deviations from PPP.
We assume there are two countries: Home and Foreign (values for Foreign are denoted by an asterisk). Thus, w denotes the Home wage and w* denotes the Foreign wage, each measured in the respective currencies. The Home exchange rate is E (units of Home currency per unit of Foreign currency). There are two goods. Each good is produced competitively and labor is the only input needed. One is a nontraded, service good (say, a haircut), denoted N, and its trade costs are effectively infinite. The other is a costlessly tradable good (say, a DVD player), denoted T, that has no trade costs at all. Prices of goods will be denoted p and p*, each measured in the respective currencies, with subscripts T and N to denote traded and nontraded goods.
A Simple Model The model can be solved in three steps, with assumptions as follows:
It may be easier to consider one country facing an exogenous world price of the traded good, and then to imagine an increase in productivity in the traded sector.
Also, requiring constant marginal products is restrictive and unnecessarily complicated. Just say that workers are paid their MPLs in both sectors and that since labor is mobile (actually, another assumption) between sectors then MPLN = MPLT.
- The traded good has the same price in both countries. This is true because trade costs are zero. For simplicity, we assume that the traded good has a price of 1 when measured in Home currency (say, dollars). This is its price in Home and Foreign, so
In our example, the DVD player sells for $1 everywhere. - Productivity in traded goods determines wages. Suppose that one Home worker can make A units of the traded good (the DVD player) per hour. Then the worker’s hourly wage w will be equal to $A because each unit of the good sells for $1 and competition means that the wage will equal the value of the output produced by each hour of labor input. Similarly, if Foreign workers can make A* units of the traded good per hour, their dollar wage Ew* will be equal to $A*. Thus, wage levels in each country are equal to productivity levels:
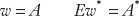
In our example, if Home workers make ten $1 DVD players per hour, their hourly wage is $10 per hour. If Foreign workers make only five per hour, their hourly wage is $5. - Wages determine the prices of nontraded goods. Crucially, we assume that the level of productivity in nontraded goods is a fixed constant, the same everywhere, equal to 1. In our example, it always takes one hour to get a haircut in Home and Foreign, but with the wages given previously, this means the cost of a haircut will equal exactly one hour of labor. In general, the dollar price of the nontraded good in each country equals the wage, so pN = w and
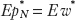 . Because these wages are given by productivity (as we saw in the second step),
. Because these wages are given by productivity (as we saw in the second step),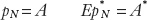
To continue our example, if the productivities are 10 and 5 in Home and Foreign, the hourly wages must be $10 and $5, respectively, and Home haircuts will cost $10 and Foreign haircuts $5.
The conclusion from these three assumptions? Countries with higher traded goods productivity will have relatively high wages and hence relatively high prices of nontraded goods. This means they will also have relatively higher overall price levels, depending on how large the share of nontraded goods in the consumption basket is. To see this, suppose the nontraded goods share of consumption is n (so the traded share is 1 − n).
456
Students will panic with this formula, so explain the intuition: Productivity growth in the domestic traded-goods sector raises wages. This raises costs in both sectors, but traded goods prices can't increase. Nontraded goods prices do increase, however, raising the price level and causing a real appreciation of the domestic currency.
Changes in Productivity Now suppose Home productivity A increases, with the proportional change given by ΔA/A. What happens to the Home price level? The price of traded goods is unchanged and stays at 1, but the price of nontraded goods is equal to A and it rises. Taking the weighted average, we can compute the (percentage) change in the Home price level as

By the same logic, the same is true for Foreign: a change in its dollar price level will result from a change in foreign productivity:

The last two equations are intuitive. For our example, a 1% rise in Home DVD player productivity A will raise Home wages w by 1%; therefore, Home haircut prices rise 1% and, because these haircuts have a weight n < 1 in the overall basket, the overall price index rises by n%.
By putting together these last two results, we can solve for the change in the real exchange rate q. Recall that q is equal to EP*/P, so the percentage change in q is given by the percentage change in the numerator EP* minus the percentage change in the denominator P. But we have just computed those changes in the last two equations. Hence, subtracting the first equation above from the second, the change in the real exchange rate is given by

Thus, relative productivities in the traded goods sector drive relative prices, through their effects on wages and prices in the nontraded sector.
Generalizing In this example, we examined the effects of productivity and wages on the prices of DVD players and haircuts. The analysis applies to all goods, however, and it can explain the cheap Big Mac story told earlier. A country has relatively low wages because it has relatively low labor productivity in traded goods. Low productivity and wages hold down the prices of nontraded goods and the nontraded part of the overall price level.
457
Emphasize this result.
This equation describes a relationship between productivity and the real exchange rate known as the Balassa-Samuelson effect, named for the economists Bela Balassa and Paul Samuelson:
When compared with other countries, a country experiencing an increase in productivity will see wages and incomes rise and will see its real exchange rate appreciate, meaning that its price level will rise.4
Overvaluations, Undervaluations, and Productivity Growth: Forecasting Implications for Real and Nominal Exchange Rates
The Balassa-Samuelson model makes a firm prediction that is supported strongly by evidence: price levels are higher in rich countries. The scatterplot in Figure 22-2, panel (b), showed this fact, and we zoom in to examine a part of it in Figure 22-3.
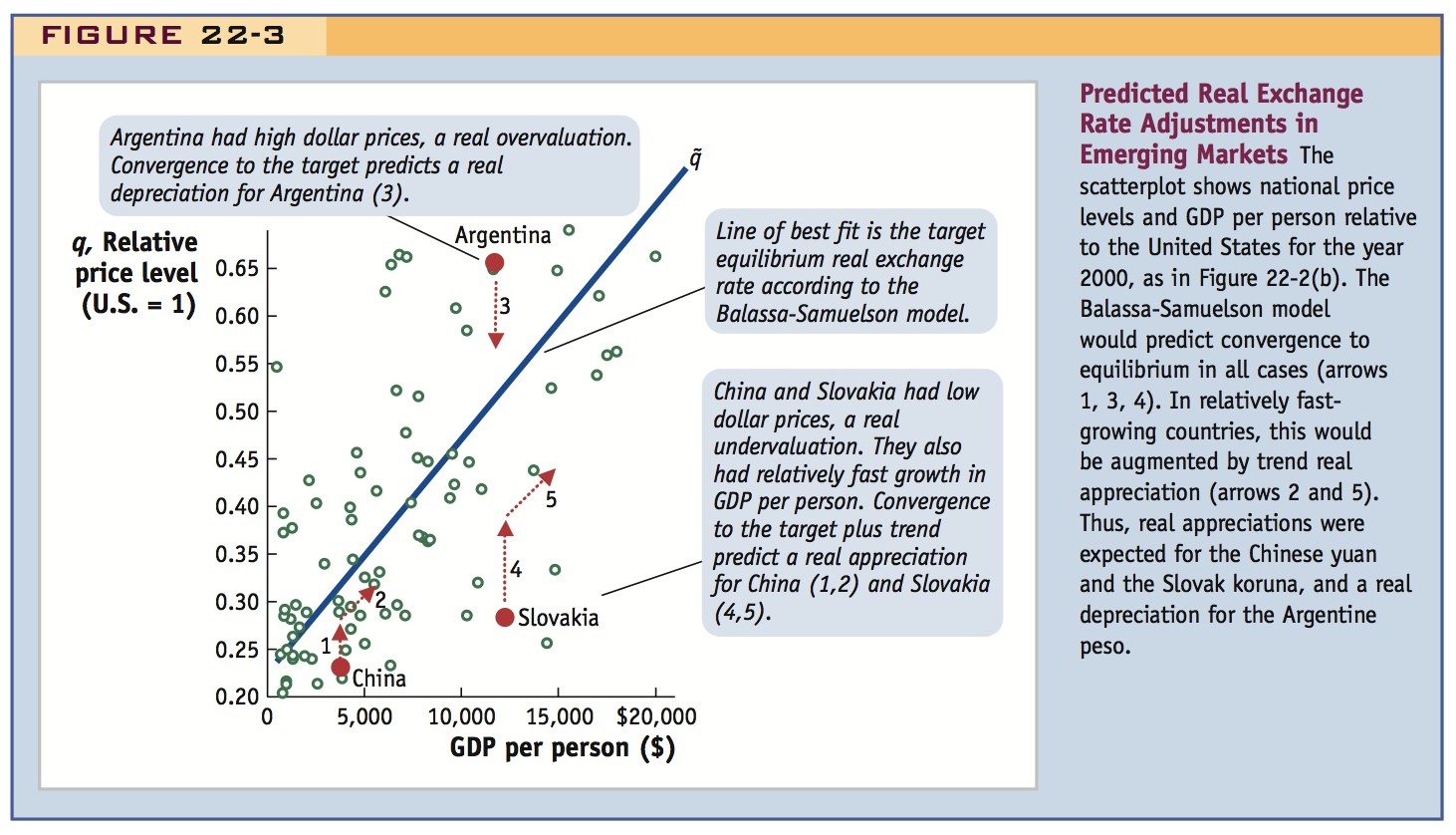
In such a figure, a point on the line of best fit is the predicted equilibrium real exchange rate 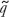 of the Balassa-Samuelson model. Figure 22-3 plots the U.S. real exchange rate against each foreign country—it shows foreign dollar prices EP* relative to U.S. prices P. So an increase on the vertical axis is a rise in the relative price of foreign goods: it is a U.S. real depreciation, or a foreign real appreciation. The actual data do not sit precisely on the line of best fit. That is, the observed real exchange rate q may differ from its equilibrium value
of the Balassa-Samuelson model. Figure 22-3 plots the U.S. real exchange rate against each foreign country—it shows foreign dollar prices EP* relative to U.S. prices P. So an increase on the vertical axis is a rise in the relative price of foreign goods: it is a U.S. real depreciation, or a foreign real appreciation. The actual data do not sit precisely on the line of best fit. That is, the observed real exchange rate q may differ from its equilibrium value 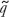 .
.
458
As we saw in the long-run exchange rates chapter, the typical real exchange rate q can from time to time experience an overvaluation or undervaluation relative to its equilibrium value 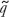 . But there we assumed that the equilibrium value was 1, as predicted by PPP theory. Here, the equilibrium
. But there we assumed that the equilibrium value was 1, as predicted by PPP theory. Here, the equilibrium 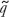 isn’t necessarily 1, and is given the Balassa-Samuelson theory.
isn’t necessarily 1, and is given the Balassa-Samuelson theory.
Here, we judge deviations from equilibrium by looking at the distance from the equilibrium, that is, from the line of best fit. For example, if actual q is 10% above predicted 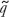 , then foreign prices are “too high”: we would say that the U.S. real exchange rate is undervalued and the foreign real exchange rate overvalued relative to the equilibrium level
, then foreign prices are “too high”: we would say that the U.S. real exchange rate is undervalued and the foreign real exchange rate overvalued relative to the equilibrium level 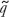 .
.
We can now begin to see how the Balassa-Samuelson theory can improve our theory of exchange rates in the long run and the forecasts that depend on such a theory.
Forecasting the Real Exchange Rate By comparing actual exchange rates with their predicted equilibrium values, forecasting the real exchange rate can be broken down into two problems: (1) how quickly q will return toward its equilibrium value 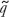 and (2) how quickly the equilibrium value
and (2) how quickly the equilibrium value 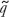 will change over time as a result of productivity changes. In other words, q may be heading toward a target level
will change over time as a result of productivity changes. In other words, q may be heading toward a target level 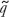 , but our model tells us that it might be a moving target that is moving along a trend. This means that real exchange rate prediction must be broken down into two parts.
, but our model tells us that it might be a moving target that is moving along a trend. This means that real exchange rate prediction must be broken down into two parts.
For example, suppose q is currently 0.5 but the Balassa-Samuelson model says the equilibrium value of 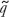 is 0.6. Clearly, q is predicted to rise by 0.1, or by 20%, to return to equilibrium (0.1/0.5 = 20%). How long will this take?
is 0.6. Clearly, q is predicted to rise by 0.1, or by 20%, to return to equilibrium (0.1/0.5 = 20%). How long will this take?
Convergence The first step is to figure out the speed of convergence to equilibrium. Empirical estimates indicate that real exchange rate deviations from equilibrium might decay slowly: the consensus “half life” of deviations from PPP has been reported to be five years. For illustration, we adopt this rule of thumb estimate in the rest of this section. Thus, in our example, if half of the 20% gap is likely to be closed over five years, then over five years, q would rise by approximately 10% from 0.5 to 0.55, an increase of about 2% per year.
Trend The second step is to figure out whether 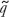 is a moving target and forecast what its trend rate of growth will be. The Balassa-Samuelson theory shows how. In our example, suppose that the home country is expected to grow rapidly, with GDP per capita and wages rising; then
is a moving target and forecast what its trend rate of growth will be. The Balassa-Samuelson theory shows how. In our example, suppose that the home country is expected to grow rapidly, with GDP per capita and wages rising; then 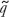 could be much higher than 0.6 in five years’ time. For example, if the nontraded share is 0.4, then Equation (11-1) says that a country’s
could be much higher than 0.6 in five years’ time. For example, if the nontraded share is 0.4, then Equation (11-1) says that a country’s 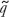 will rise 0.4% for every 1% of real GDP per capita growth in excess of the U.S. growth rate. So if a country is growing at, say, 8% per year faster than the United States, then
will rise 0.4% for every 1% of real GDP per capita growth in excess of the U.S. growth rate. So if a country is growing at, say, 8% per year faster than the United States, then 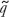 should be rising by 0.4 × 8%, or 3.2% per year.
should be rising by 0.4 × 8%, or 3.2% per year.
Convergence + Trend For this numerical example, we would conclude that the observed real exchange rate q is likely to increase at 2% per year toward its equilibrium and to increase at a further 3.2% a year due to the upward drift of that equilibrium, resulting in a predicted real appreciation for the foreign country at a rate of about 2 + 3.2 = 5.2% per year. (Note that adding growth rates in this way is only an approximation.)
Forecasting the Nominal Exchange Rate This kind of real exchange rate forecast can then help us predict nominal exchange rates, an essential component in the asset approach to exchange rates. How?
By definition, the real exchange rate is q = EP*/P; by rearranging, we find E = qP/P*, and we have an expression for the nominal exchange rate. When PPP holds, this equation becomes E = P/P*: under PPP, the real exchange rate q equals 1, and the exchange rate is equal to the ratio of national price levels.
459
This forecasting example is neat, and students will enjoy it. However, here is another possible extension that links back to the monetary model: Use E = qP/P* combined with the money market equilibrium conditions to generalize the solution for the exchange rate back in Chapter 14 (Equation 14-3). Then show how productivity growth will affect E both via Balassa-Samuelson and by changing income and hence money demand.
When PPP doesn’t hold, however, we have to worry about possible changes in q. Since E = qP/P*, then taking rates of change, we find
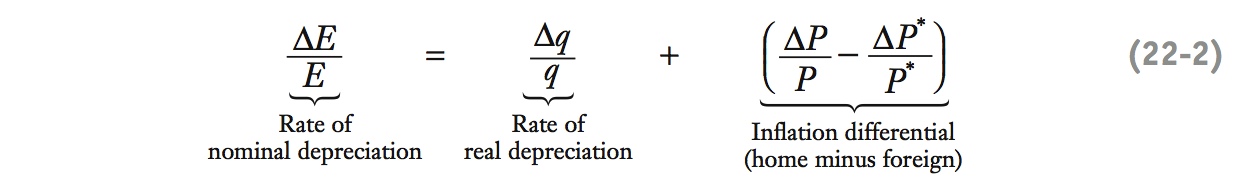
In the long-run exchange rates chapter, we saw a simpler version of this expression: PPP forced q to be constant and equal to 1, and the first term on the right vanished. We were left with a result, known as relative PPP, which says that changes in nominal exchange rates depend on inflation differentials alone. Taken literally, forecasters can then focus just on inflation forecasts.
When the Balassa-Samuelson effect is present, PPP fails, but we can still forecast future exchange rate changes using Equation (11-2). In using this equation, however, we not only have to forecast inflation, we have to forecast changes in the real exchange rate, too. Thus, in real-world financial markets, foreign exchange traders have to pay attention to many macroeconomic forecasts before forming an expectation about how E is likely to evolve over time.
Adjustment to Equilibrium Finally, we note that the Balassa-Samuelson model does not tell us how the real exchange rate will adjust. Suppose we have forecast a 1% real appreciation (−1% change in q). In Equation (11-2), this could imply either a 1% nominal appreciation (−1% on the left) or an extra 1% of home inflation over and above foreign inflation (+1% on the right), or some combination of the two.
Thus:
- If the model says there is currently a real undervaluation, either home goods prices have to rise or the value of the home currency has to rise—there is no other way to make home goods more expensive.
- If the model says there is currently a real overvaluation, either home goods prices have to fall or the value of the home currency has to fall—there is no other way to make home goods less expensive.
Applies this forecasting method to three episodes since 2000: China, Argentina, and Slovakia.
China is a great example. Inflation was having the same real effect as letting the currency appreciate--to the chagrin of some Chinese businessmen.
Real Exchange Rates in Emerging Markets
To see how we can use these ideas to make forecasts of real and nominal exchange rates, we examine three cases in Figure 22-3 that were in the news a few years ago. The data we use are for the year 2000, which allows us to look at subsequent events and see how well the predictions of the model turned out in the following years.
China: Yuan Undervaluation? The Balassa-Samuelson model predictions: in 2000 the real exchange rate with China was q = 0.231, well below (0.088 below) the predicted equilibrium level of 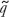 = 0.319. The yuan was undervalued according to the model and would have to experience a 38% real appreciation (0.088/0.231) against the U.S. dollar to close the gap. Using our old rule of thumb, half of this gap or 19% would be eliminated in five years, implying an approximate 3.5% annual increase in q due to convergence.
= 0.319. The yuan was undervalued according to the model and would have to experience a 38% real appreciation (0.088/0.231) against the U.S. dollar to close the gap. Using our old rule of thumb, half of this gap or 19% would be eliminated in five years, implying an approximate 3.5% annual increase in q due to convergence.
However, in addition, China was a fast-growing economy at this time and its GDP per capita was growing about 6% per annum faster than U.S. GDP per capita. So the real exchange rate would have to appreciate even more due to Balassa-Samuelson effects. Figure 22-3 suggests that every 1% gain in GDP per capita is associated with an approximate 0.4% real appreciation (as expected if the nontraded share were 0.4). So a 6% differential growth rate per year (China minus United States) would imply a further 0.4 × 6 = 2.4% per year real appreciation in the yuan due to the trend of the moving target.5
460
What actually happened: Adding up both effects, the model predicts a real yuan appreciation of 3.5 + 2.4 = 5.9% per year. As noted previously, this would imply either a nominal appreciation of the yuan against the dollar, or higher inflation in China. Inflation did start to rise in China, up to as much as 4.1% in 2004, although the data are not considered terribly accurate. This was not that much higher than U.S. inflation. Until mid-2005 China pegged the yuan to the dollar but then decided to switch to an unofficial crawling peg, allowing the yuan to appreciate gradually against the dollar, but very slowly. Many commentators saw this as a response to protectionist pressure in the United States, where cheap Chinese imports were raising hackles. But the Chinese had reasons of their own to let the yuan rise: to keep domestic inflation at a reasonable level.
Argentina: Was the Peso Overvalued? The Balassa-Samuelson model predictions: Figure 22-3 clearly shows that Argentina’s currency was overvalued in 2000: Argentina’s price level was 0.656, but the predicted equilibrium level of 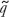 was 0.512. For a country at that level of GDP per capita, Argentina’s dollar prices would have had to fall by 22% to reach that equilibrium. Argentina’s growth had slowed after 1998, so, unlike in the China case, very little rise in the equilibrium
was 0.512. For a country at that level of GDP per capita, Argentina’s dollar prices would have had to fall by 22% to reach that equilibrium. Argentina’s growth had slowed after 1998, so, unlike in the China case, very little rise in the equilibrium 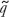 could have been expected (which would have mitigated the need for a fall in actual q).
could have been expected (which would have mitigated the need for a fall in actual q).
What actually happened: Argentina was pegging the peso to the dollar at 1:1, so adjustment had to come through a fall in Argentine prices relative to U.S. prices. With U.S. inflation at only 2%, this would happen slowly unless Argentine prices actually dropped. Unfortunately, this deflation process was slow and politically painful, involving wage and price cuts in an economy that was far from liberalized and competitive. The overvalued exchange rate was also hurting the demand for Argentine goods. Although the peg held for a long time, the country was driven into crisis by fiscal and financial sector problems. In the crisis of 2001–02, the peso depreciated to three per dollar: the overvaluation was eliminated, and then some.
Slovakia: Obeying the Rules? The Balassa-Samuelson model predictions: Figure 22-3 also shows Slovakia. Like China, Slovakia was a fast-growing country, part of a group of countries in Eastern Europe lined up to join the European Union (EU) and ultimately the Eurozone. Slovakia’s real exchange rate was q = 0.282 in 2000 and undervalued relative to the predicted equilibrium 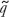 = 0.534. Here, q needed to rise by 89% to reach equilibrium. Using our rule of thumb, half of this gap, or 45%, would be closed in five years, implying a real appreciation of about 7.5% per year. In addition, fast GDP per capita growth relative to the EU probably added another 1% to 2% on top of that, as in the China case, as a result of the moving target. Thus, the expected real appreciation would have been 8% to 10% per year.
= 0.534. Here, q needed to rise by 89% to reach equilibrium. Using our rule of thumb, half of this gap, or 45%, would be closed in five years, implying a real appreciation of about 7.5% per year. In addition, fast GDP per capita growth relative to the EU probably added another 1% to 2% on top of that, as in the China case, as a result of the moving target. Thus, the expected real appreciation would have been 8% to 10% per year.
What actually happened: Slovakia notched up high rates of real appreciation of between 5% and 10% per annum from 1992 to 2004, as did many other countries in Eastern Europe.6 The situation was like that in China: it required some combination of nominal appreciation and inflation. But Slovakia (and many of its neighbors) also wanted to join the euro. As we saw in the chapter on the euro, the Maastricht criteria would require Slovakia to peg to the euro (no appreciation) and keep its inflation within limits (within 2% of the “best” in the EU). Our model suggests this would be impossible: the koruna would have to appreciate or Slovakia’s inflation would have to accelerate! As an exercise, you may wish to explore in more detail what actually happened. (See the second Net Work problem at the end of this chapter.)
These are neat examples too. Highlight the fact that adjustment must occur either through the nominal exchange, or prices, or a combination of the two.
461
Conclusion
4. Conclusion
PPP fails even in the long run because of trade costs. Balassa-Samuelson explains why this happens and why rich countries have higher prices; it can also be used to make improved forecasts of real and nominal exchange rates.
In general, PPP does not hold. Goods prices are not the same in all countries. Arbitrage fails, most likely because of trade costs. The Balassa-Samuelson theory can explain how prices vary when goods are not traded and why rich countries have higher price levels. As countries get richer, their wages rise, driving up the prices of their nontraded goods (which use local labor as an input). This will drive up the overall price index and will cause the real exchange rate to fall—that is, a real appreciation. The theory finds strong empirical support and can be used to make better models of real and (hence) nominal exchange rates, with improved predictions, in situations in which an assumption of PPP is inappropriate.