Chapter 1. Figure It Out 10.1

1.1 Screen 1 of 4

true

A firm with market power faces an inverse demand curve for its product of P = 100 – 10Q. Assume that the firm faces a marginal cost curve of MC = 10 + 10Q.

If the firm cannot price discriminate, what is the profit-maximizing level of output and price?

Question

The profit-maximizing output is 607M7xmPORU= units.

The profit-maximizing price is $ /HOzig3d1HHP0SbU

To find the profit-maximizing output, first find marginal revenue, and then equate marginal revenue and marginal cost. Marginal revenue starts at the same point as the inverse demand but has twice the slope, so MR = 100 – 20Q. Setting MR = MC, 100 – 20Q = 10 + 10Q. So, Q = 3. Substitute 3 for Q in the demand curve to find the profit-maximizing price, $70. For further review see section “Profit Maximization for a Firm with Market Power”.

1.2 Screen 2 of 4

Figure A

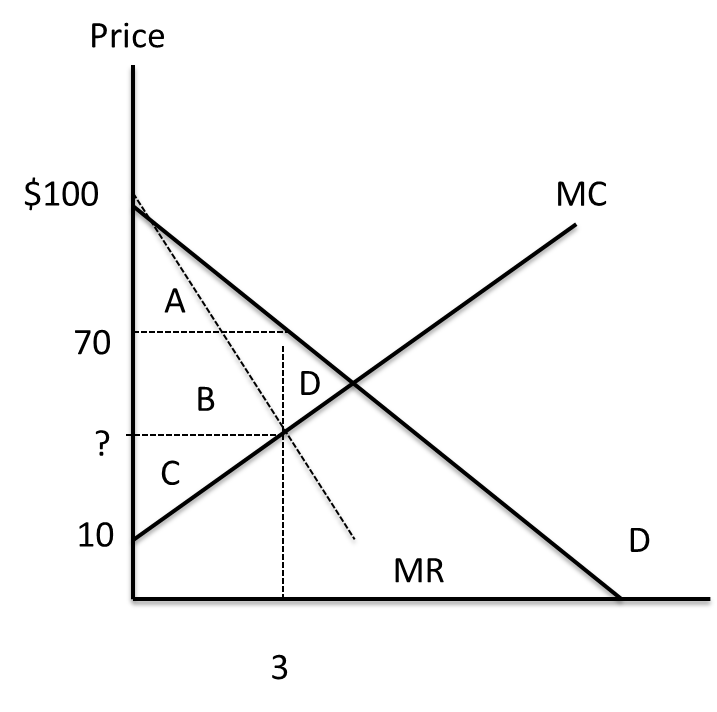
The graph above represents a market in which one firm has market power. If the firm cannot price discriminate, how much consumer surplus will buyers receive? How much producer surplus will the firm receive? How much deadweight loss will the market power create?

Question

Buyers will receive $ 1uolHciWnBAn2yh/ of consumer surplus.

The firm will receive $ jHoSZOeOG97Cis9A of producer surplus.

The deadweight loss from market power is $ 3guN5oV67cVOPGWYcGflMYeVwfwffICvCXfsbA==

Consumer surplus is the area above the price and below the demand curve, shown as area A in the graph. That triangle is $30 tall and 3 units wide, so its area is 0.5 × $30 × 3, or $45.
Producer surplus is the area below the price and above the supply curve, shown as areas B + C in the graph. To determine those areas, plug 3 units of output into the marginal cost function to find that MC = $40. So, area C is a triangle $30 tall and 3 units wide, for an area of 0.5 × $30 × 3, or $45. Area B is a rectangle $30 tall and 3 units wide, or $30 × 3 = $90. Therefore, areas B + C = $90 + $45 = $135.
The deadweight loss is surplus that would be created under perfect competition but not with a market in which a firm has market power. That area is shown as D in the graph. To find area D, find the perfectly competitive output level by equating marginal cost and demand: 10 + 10Q = 100 – 10Q, or Q = 4.5. So, area D is a triangle $30 tall and 1.5 units wide, for an area of 0.5 × $30 × 1.5, or $22.50. For further review see section “The Winners and Losers from Market Power”.

1.3 Screen 3 of 4

Figure B

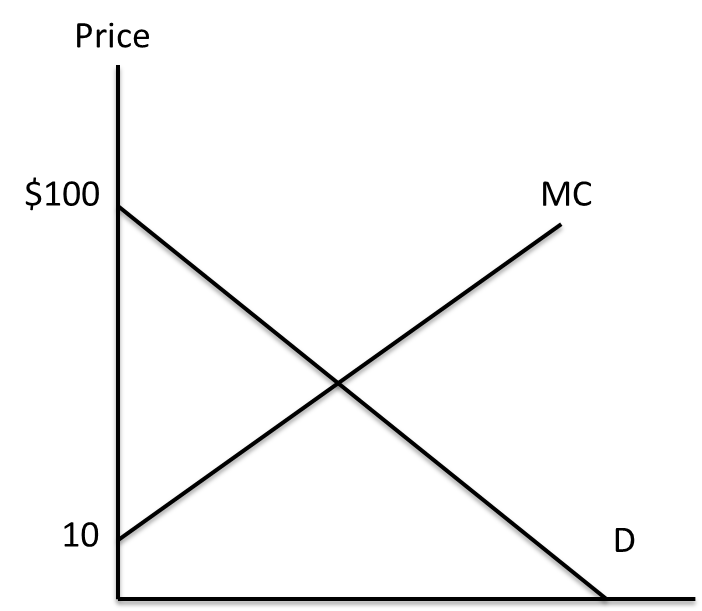
If the firm represented in the picture above has the ability to practice perfect price discrimination, what is the firm’s output?

Question

The perfect price-discriminating firm’s profit maximizing output is FpN+1zn6s3w=

A firm practicing perfect price discrimination will sell any unit for which the price the buyer is willing to pay (represented by the demand curve) is greater than or equal to the marginal cost of production, and will stop selling when P = MC. That occurs where the demand curve intersects marginal cost, or when 100 – 10Q = 10 + 10Q. Solve to find that Q = 4.5. For further review see section “Direct Price Discrimination I: Perfect/First-Degree Price Discrimination”.

1.4 Screen 4 of 4

Figure C

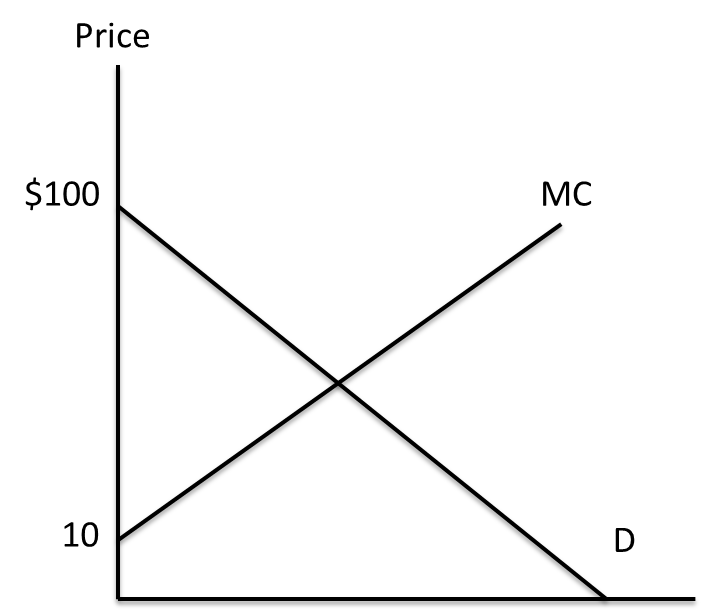
If the market above is monopolized by a firm practicing perfect price discrimination, what are the levels of consumer and producer surplus? What is the deadweight loss from market power?

Question

Buyers will receive $ ZG0JgDx77WI= of consumer surplus.

The firm will receive $ Iobm71hufTL0Rkb6fz6IIt2uyOI= of producer surplus.

The deadweight loss from market power is $ ZG0JgDx77WI=

A perfectly price-discriminating firm charges each buyer his or her maximum willingness to pay, so each consumer receives zero surplus.
Perfect/First-Degree Price Discrimination”.