Chapter 6. Binocular Disparity

6.1 Title slide

Demonstration 6.1

true

You must read each slide, and complete any questions on the slide, in sequence.

true

title

Binocular Disparity

Explore how the binocular disparity of an object's retinal image changes as you change the depth of the object.

CLICK ANYWHERE TO BEGIN

This looks like a photo of a man holding up the Leaning Tower of Pisa. But if you had been standing beside the photographer when he shot this picture, you would have perceived the tower as being much farther away than the man, because your visual system would have used the slightly different views in the two eyes to judge the relative distances of these two objects. A photo gives you only one view of a scene, and sometimes that view is misleading.
Photo: Bettmann/Getty Images

What Is Binocular Disparity?

The retinal images in your two eyes are slightly different, because your eyes view the scene from slightly different positions (about 6 cm apart). The difference in the left and right retinal images is called binocular disparity.

The relative positions of objects in the two retinal images can be understood in terms of corresponding and noncorresponding points. A point on the left retina and a point on the right retina are corresponding points if they would coincide if the two retinas were superimposed. Conversely, noncorresponding points wouldn't coincide if the retinas were superimposed. Fixated objects produce retinal images on corresponding points, as do all objects that lie on an imaginary surface called the horopter, which passes through the point of fixation. This is shown in Figure 1, where the fixated red object is on the horopter, so the retinal image of that object falls on the fovea of each eye (points F and F'). The blue object is also on the horopter, and it also produces retinal images at corresponding points (B and B'). Objects that are either nearer or farther than the horopter—like the brown and green objects—produce retinal images on noncorresponding points (A and D' for the green object, C and E' for the brown object).

This figure also illustrates the three types of binocular disparity. Objects on the horopter, like the fixated red object and the blue object, are said to have zero disparity. Objects nearer than the horopter are said to have crossed disparity, and objects farther than the horopter are said to have uncrossed disparity. The observer sees the brown object to the right of the red object with the left eye and to the left of the red object with the right eye. This right–left, left–right aspect accounts for the term crossed disparity. The observer sees the green object to the left of the red object with the left eye and to the right of the red object with the right eye. This left–left, right–right aspect accounts for the term uncrossed disparity.

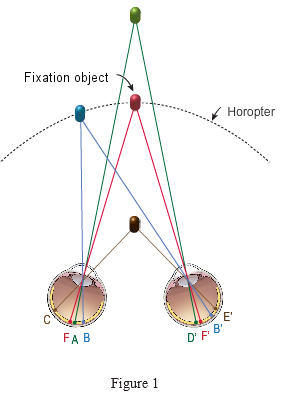
The magnitude of the binocular disparity is the distance between the images of an object on the two retinas. For example, if the retinas were superimposed, the distance between the two images of the brown object would be greater than the distance between the two images of the green object; thus, the magnitude of the brown object’s binocular disparity is greater than that of the green object.

The visual system uses the type and magnitude of objects' binocular disparity to determine the relative depth of objects in the scene.

6.2 Explain - dnd

activity_6_1_slide_2

You haven't explored the activity on this screen. However? you can return to this screen at any time. Are you sure you want to leave?

The blue and red objects are the same size, and the observer's eyes are fixated on the red object. Comparison of the left eye and right eye views illustrates binocular disparity: the difference in the position of an object in the retinal images in the two eyes. An object closer to the observer than the horopter produces crossed disparity: in order to switch her focus to that object, the observer would have to further "cross" her eyes. An object farther from the observer than the horopter produces uncrossed disparity: in order to switch her focus to that object, the observer would have to further "uncross" her eyes. An object on the horopter produces zero disparity. The magnitude of the disparity is the distance between the images of the object in the two views (imagine superimposing the views to determine this distance).

Drag the blue object up and down to explore these relationships.

6.3 Explain

explain_text

What Is Binocular Disparity?

The retinal images in your two eyes are slightly different, because your eyes view the scene from slightly different positions (about 6 cm apart). The difference in the left and right retinal images is called binocular disparity.

The relative positions of objects in the two retinal images can be understood in terms of corresponding and noncorresponding points. A point on the left retina and a point on the right retina are corresponding points if they would coincide if the two retinas were superimposed. Conversely, noncorresponding points wouldn't coincide if the retinas were superimposed. Fixated objects produce retinal images on corresponding points, as do all objects that lie on an imaginary surface called the horopter, which passes through the point of fixation. This is shown in Figure 1, where the fixated red object is on the horopter, so the retinal image of that object falls on the fovea of each eye (points F and F'). The blue object is also on the horopter, and it also produces retinal images at corresponding points (B and B'). Objects that are either nearer or farther than the horopter—like the brown and green objects—produce retinal images on noncorresponding points (A and D' for the green object, C and E' for the brown object).

This figure also illustrates the three types of binocular disparity. Objects on the horopter, like the fixated red object and the blue object, are said to have zero disparity. Objects nearer than the horopter are said to have crossed disparity, and objects farther than the horopter are said to have uncrossed disparity.

The magnitude of the binocular disparity is the distance between the images of an object on the two retinas. For example, if the retinas were superimposed, the distance between the two images of the brown object would be greater than the distance between the two images of the green object; thus, the magnitude of the brown object’s binocular disparity is greater than that of the green object.

The visual system uses the type and magnitude of objects' binocular disparity to determine the relative depth of objects in the scene.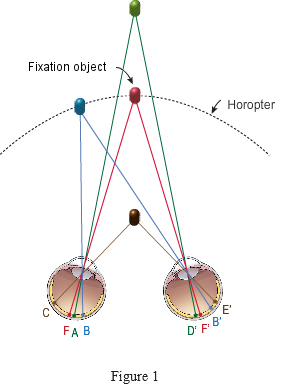

6.4 Test - single choice

You must select an answer and then click SUBMIT before you can click proceed to the next screen.

test_single_choice

Select your answer to the question below. Then click SUBMIT.

Question

ymgjAFCtbCNp3VGjg7eLDY+3Z2/gp5dAvZLSSvZgsPf69GeyLXfkgL27bLCesaZ0Z6DcWYlRbNTGNHbt3SknBMHbM5rO7drTbKFMlIfvavL0rcT/suYlBXGmBIfLO4/SwS9oCQqhwoEZ0X0Y7GIzPvDHUle66sCIiKoQkojxOJoG4p0QChL1H9rrPIy/8QUH6WHVSKG1W+n39aFv0EKR0MM2zfurEsOVQXuwzexCFA38GwXgNvMGfNsZxLgMe10S2TebKzxdCdd0IhfeCZdTfY7D2Fd0RP291e96i0n631sJIAb0t5XKx71k54f6pJdS41I3CnDN2WCchVkF3mTOzmmEyrLs7rw2IwmwLlEnLNGO4qUY5hZj5gix79DxtWhdts+iqWcLw/NepFH8JA6LbEbPOHApuGc4eYlLDghZqYACZqGFrA3qNRCoWfgBu0bdGRz4A5plwwbgGZDl6E/ng/stBCV3PlrjsTVUW+6FOI4Wvvth2drKiba9Zopr8Hes/a3KVdSlMi5zjSxAy8cACDcuwgZdBO9TrHNuGDLLw9J/cJm/2AtTkBuhOHs6DAoDMJ+Ug0JUKgbPXsf0iiYeOeh7n2UQhF4XrfiCRL9U/Qdnxqbyie3mIaqS+YaXn4sNNi+DRMjBdQ8K9moDzusGPVnTb8Jx8w0/dkkDubYGSwfzrqJ5JBwziu6SOoVLUbKx/QqBoA7w0iWLWeF7vudd7ANsa9COQJQKcR1M+WgUEw99MLs3YlWTeTnkwi4WaL7XYLGxEeHlecAv0z+bFl6sjpULzJMQDd74s9fgVpbD9immIzsiJ1N44sUWEdEdn7wzp8ZNgvoNpvFIAGrdRgri0W69hLT2PPZPu657+AZBgLwVIkma

Correct! Click EXPLAIN if you want to review this topic.

Incorrect. The correct answer is D. Click EXPLAIN if you want to review this topic.

6.5 Test - single choice

You must select an answer and then click SUBMIT before you can click proceed to the next screen.

test_single_choice

Select your answer to the question below. Then click SUBMIT.

Question

Z1yxat8wwOS61eb1jMzlEjThHKJhQlAVn7nOAHQtUAUlmLjGP2hWYR5KVSLVZjnUa53pTjptGtAYK5GO8LXpXddBGz+KJe5oH2SkVr6jHFz5upy2ASNoMGvswKhRM6RpgdTThkd/NmGVbw4unAJMMjMRlXYGNgcO1Ba6Us3z340b8cI+CquVLpb0POifuZv3mzE3M0x22JdCIE2QTJZsbzevIfdtCis1TZtTw4/qt2ft4TBEjkr2HxJttyYeyaUaaLicegV9z+JOUGuOsZ2asDu0ieQTdSp91qvDlIqkcrWnuX5sG8AkhQpDTELQ5H5DDG5Ux14x7GqptLoX0EZ2W8h1Gi4R1I2j6XNH6EQzwqAuJxr50niBQ6hUYniT9GgxdnJ2orzkW54P1K94QFCvHUj4R53TCRRPwwhAkF3OC/XgU8v4PQ5sXwftmMU3waTqTbsOBJnuYVJafqachKMAlLdWg3KApMvWJrsKFABZMl7kRNzlKOMCn74AoXhPcvgP2YwT4ORdm3Rnmqkr8Os+sMk9vmZ/4WdtE34fcKyD00e02mI5RYApg2W+NJUUOAmJgbxCFuUE3tRMDaBcgLBiaO+qhU7LgA7ftbcF93smWV9vaZaC0xqDw7RsvikOdUbzxM99vCM6i/3FybAXTJcSgiB95Ng1knc5p1VHcgRdHwDahFATXyUybwt2ECYhmINeTVWz4FgaKZZ+095B/YYCvbGGf3dWtZvsPAlFcAtR2Yv9OMeHNPJ3T6p5lv+RJzZhPkWN1ejSLHsNT4s26h+ad4TXkzHgGOEEjRHyml8af/OvPbTxjue+Uk1cJCVWYEUMbDafz1TMQieCAgMycjWEkV62T1NJskwP8Xp8JA6uv1cD/Yh6ryedd6vceC2Um5fAeFH6hDf3in2uuiSiYKMkJfA0uRmK7FXYTxwZUVmwg3vv8jWrMdMnY/IzOe0Z7lFGYLgScsQIWZT0fMPxlkYRMv79VrQK3l20ho55GU7xX6bSJ2LUMoVXYkJ2AJ++IQX4APLVs9NJs4IO2nfvg1EZu+EGOtEfaF2UyywcmtL+wh/szv0Ow2xg+eBoK98H0pIMh4ZOHzNq8Ec=

Correct! Click EXPLAIN if you want to review this topic.

Incorrect. The correct answer is B. Click EXPLAIN if you want to review this topic.

6.6 Test - single choice

You must select an answer and then click SUBMIT before you can click proceed to the next screen.

test_single_choice

Select your answer to the question below. Then click SUBMIT.

Question

HYXioSbgKnGXJQmNrC0tEuP+A1eAfuk1cNoK30mM7nkNWsrxb3NyGmbjG18z20n+oaDCqeY9eAIyJvDxOwrNkIrtJ3WZFOFQOUNUgBBHceJ61Cyz6bCw1j9gjryFsEfx0+TsZW9xDK+HQt/48MFRXzPyGI6ELaMHhfyJ+GsBpouJD7XsS30zcmXFza73HzeBkJ9hMw0LglMKz8f0eHMOD1yrt/LhA1nj6FkBN0dEo7z6/xOzzB/wYrLT8GKCi6yLVdKBghT52RXhOaAr+6f9zyfueEZ1G002c9frHmA+TlmsZvNkY09XyDejhRBV0sOkWu4FT+h0VU97dv85J8VotoFij5sQcxuLI0LQeRPWAs4N801ZEfCgUaajedqO8y6mH+HDkioW6DHy1Q2nty/qaa3GphzdWAMZ/g/smFfa7CGXGr/TOESecb3B4NlB7e5NyKMgx7EaQ8QNSuYzKfU30j5Wdo/nzwTIokoB7ACw63ITB8mEX2E/d0GpNGjRT72MLvVj1MkbYO1H0OH/BvjJGIKz08AGi55T+tfpLKcDgE365rVtOTRv7HoUf6VOVkLnPglPnt5LKQi7nPdWNfyVfKdDjyOht8AaK7BrJMCmfRZXoS+XxKY56mxK2pyHdIAcVx7JtYxnR9nsYlnGgd3I1IN4Yx+Wb07wMJvBvlsWa3jgn2jdKTFGhZaTiiuHHJuCZzGhexHSYwgd0DcRV+SM0UdXruTQPq7oc6I90m+v3y2D9ggUAcWl7eYcPP2zCKfvsO5MHfWY27BPQ299JqvrM8mYy39KxLr4i1irGIIaa8tIuuRFTwRQRVTQIXegT9EMBSMhpLWun3g89w7JNarpSJogEWbgE9Kdua4kmiFnVAPzqBdo5FXGUuPFYWW8afJ/f8nC6lwlTof+sMIaM5dNvmRN2Ob8s6NFVQZ//ctExhGiPIF9wF0GTm4/LfYjgIG3KO5yibEN+mzyReVBRF+TQgVAHkTgRlyifUI1L9jN8m1+hB0XMg1e8C0i/XVH8rtqErMKTVDzVYTlAo7wS3MVXMWcyDlB3hEIny3gD8fCrwJqBQPwC7IjVA==

Correct! Click EXPLAIN if you want to review this topic.

Incorrect. The correct answer is C. Click EXPLAIN if you want to review this topic.

6.7 Activity completed

Activity Complete!

You have completed the activity
Title