12.3 Repeated Games
You now know how to find the Nash equilibrium (or equilibria) in a game in which the players make simultaneous moves. One of the examples we went over was the prisoner’s dilemma Warner Brothers and Disney faced in choosing whether to advertise (Table 12.1). Both firms would be better off if they could coordinate so that neither company advertises, but each firm has the individual incentive to advertise, so the firms are stuck making lower profits than they would if they could coordinate their decisions.
480
Now consider a perfectly sensible question: Would it matter if these firms played this prisoner’s dilemma game twice in a row? The basic problem in a prisoner’s dilemma is that neither firm has the individual incentive to cooperate with the other, even though both would be better off if they could jointly agree to do so. It seems reasonable that if players know they are going to end up in the same situation again (and perhaps again and again), they might have a better chance of coordinating their actions in a mutually beneficial way. In this section, we examine this issue and learn how to analyze repeated games that are more general than prisoner’s dilemmas.
Finitely Repeated Games
When a simultaneous game is played repeatedly, players’ strategies consist of actions taken during each repetition. If a game is played twice, players’ strategies will involve what they do in both Periods 1 and 2. Players can even develop fancy strategies that change the second-
So, how do we analyze the Warner Brothers–
backward induction
The process of solving a multistep game by first solving the last step and then working backward.
To answer this question, we first have to figure out how to think about games that are played more than once. The way to do this—
In our example game here, there are only two periods or steps, so backward induction is easy. First, we know that whatever might happen in the first period, the second period is the end of the interaction. So, when the two players get to the second and final period, they will be facing a one-
Unfortunately for the firms, the fact that the final period is a one-
Now you can probably see how things will unravel. Both players realize in the first period that they will both end up cheating in the second. It’s going to be every firm for itself. But if they know this is how things will go down, what’s the point of cooperating (by not advertising) in the first period? If a studio violates the first-
481
There goes that idea: As long as everyone knows when the game will end, repeated play doesn’t help players solve their cooperation problems in prisoner’s dilemmas. In every period, the Nash equilibrium remains the same as it was in the one-
Adding more periods won’t matter, either. Even if the game is repeated 50 more times (finishing with The LEGO Movie 53 vs. Frozen 53), the 52nd and final period will still be a one-
Not every game played across multiple periods is a repeated prisoner’s dilemma like this one. But the use of backward induction is a standard technique that can be applied to determine equilibria in other types of multiple-
Infinitely Repeated Games
It turns out the prisoner’s dilemma conundrum isn’t completely hopeless, though. There is a possible way out (or, more specifically, a possible way to cooperate). The problem with the repeated game scenario that we just discussed is that everyone knows when the last period is, so they know that all players will cheat in the last period. This knowledge causes everything before the last period to unravel. But what if the players don’t know for sure when the last period is? Or, if the players thought of themselves as playing the game over and over, forever?
The first thing you have to do in this seemingly odd game is specify a strategy for every period. This could become massively complex, given all the different orders in which a player could take actions. To make things easy, let’s consider the following simple strategy. Warner Brothers does not advertise in the first period and continues not to advertise as long as Disney doesn’t break the agreement and advertise. If Disney ever advertises, Warner Brothers abandons the deal and advertises from that point forward, forever. Disney’s strategy is the mirror image of this: Don’t advertise at first and stick to the agreement as long as Warner Brothers doesn’t advertise, but switch to advertising from then on if Warner Brothers ever advertises.
Is this set of strategies a Nash equilibrium when the game is played forever, or perhaps more realistically, where the game could end in any particular period, but the players never know when exactly the last period will come?
Because there is no final period in this game that the players can predict precisely, we can’t use backward induction. The way to think about Nash equilibria in this case is to weigh what a player could gain at any given point from trying something different from her current strategy. The logic of this approach comes straight from the definition of a Nash equilibrium: A player is doing as well as possible given the actions of the other players. If we can show that any change of strategy would make the player worse off, we know that sticking with the current strategy is a best response. If we can show this same thing for all of the players, we know the strategies result in a Nash equilibrium.
Let’s try that here. Suppose Warner Brothers decides to break with the cooperative “Don’t Advertise” strategy and starts advertising even though Disney hasn’t advertised. We know that Warner Brothers will experience a short-
Warner Brothers pays a price for its cheating ways, however. When it violates the agreement, Disney stops cooperating in the future. Having chosen to advertise in some period, Warner Brothers will have to duke it out with Disney from that point forward. Both firms will advertise all future films, and each studio will earn $150 million each time the game is played.
482
What is Warner Brothers’ payoff from cheating? It earns $350 million in the current period. In the next and every following period, it earns $150 million. Let’s allow for a firm to care somewhat less about future payoffs than current payoffs. We embody this discounting of the future with the variable d. (We will discuss the origin and impact of the discount rate and how to compute a “present value” for future payments in Chapter 14.) This variable is a number between 0 and 1, and it shows what a payoff in the next period is worth in the current period. That is, the firm views $1 in the next period as being worth $d today. If d = 0, the player doesn’t care at all about the future: Any payoff in the next period (or following periods) is considered worthless today. If d = 1, the player makes no distinction between future payoffs and today’s payoffs; they are all equally valuable. A higher d means the player cares more about the future, making the value of future payments greater.3
Let’s write down Warner Brothers’ payoff if it decides to break from the “Don’t Advertise” strategy and advertise in the current period:
Payoff from breaking away:
350 + d × (150) + d2 × (150) + d3 × (150) + . . .
Notice how payoffs further in the future are discounted more and more, because d is a per-
Payoff from sticking with the “Don’t Advertise” strategy:
200 + d × (200) + d2 × (200) + d3 × (200) + . . .
The analysis is the same for Disney’s choice of adhering to the “Don’t Advertise” strategy or reneging and surprise advertising in one period. If we can show that the payoff from sticking with the strategy is greater than the payoff from breaking away, we know that the outcome of pursuing the cooperative “Don’t Advertise” strategy is a Nash equilibrium. This is true if
200 + d × (200) + d2 × (200) + d3 × (200) + . . . > 350 + d × (150) + d2 × (150) + d3 × (150) + . . .
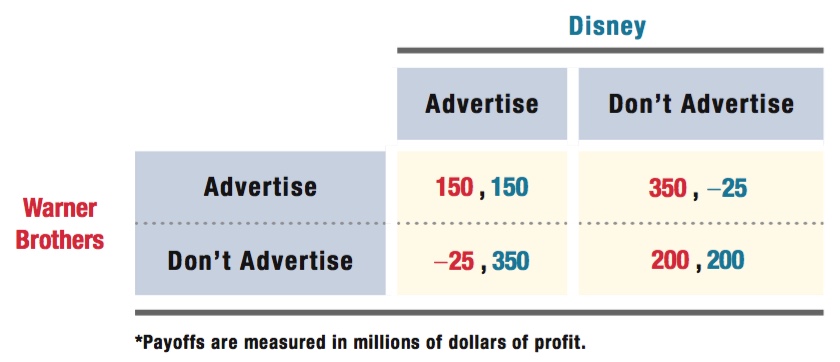
50 × (d + d2 + d3 + . . .) > 150
(d + d2 + d3 + . . .) > 3
To solve for d, we can use a simple math trick, d + d2 + d3 + . . . = d/(1 – d) for any d between zero and one (0 ≤ d > 1), and substitute it into the equation above:
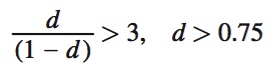
483
What does this mean? As long as Warner Brothers and Disney care enough about the future—
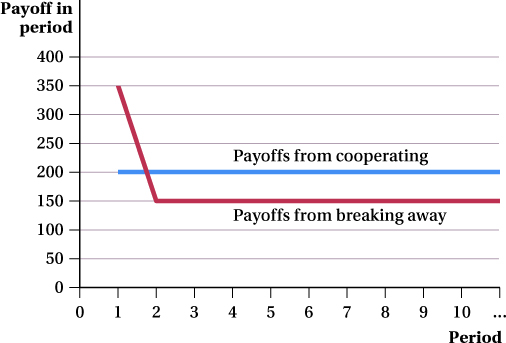
This “caring about the future” condition makes sense. Choosing to cooperate is about skipping a big payoff (profit) right now that the firm could earn by cheating on the agreement in order to get a stream of higher payoffs (profits) in the future by cooperating. This can be seen in Figure 12.1, which shows Warner Brothers’ and Disney’s payoffs in each period for the two options. Cooperating by sticking with “Don’t Advertise” leads to a steady payoff of $200 million per period. Breaking away from the agreement by advertising leads to a larger $350 million payoff in the first period but a lower $150 million payoff every period after that. The more players care about the future—
grim trigger strategy or grim reaper strategy
A strategy in which cooperative play ends permanently when one player cheats.
tit-
A strategy in which the player mimics her opponent’s prior-
By the way, the strategy we analyzed here—
484
Now we’ve identified the factors that can make coordination in a prisoner’s dilemma a Nash equilibrium: The players cannot determine when the game will end, and the players have to care sufficiently about future payoffs.
 See the problem worked out using calculus
See the problem worked out using calculus
figure it out 12.2
Suppose that two motorcycle manufacturers, Honda and Suzuki, are considering offering 10-
If the game is played once, what is the outcome?
Suppose the game is repeated three times. Will the outcome change from your answer in (a)? Explain.
Now, suppose the game is infinitely repeated and Suzuki and Honda have formed an agreement to not offer warranties to their customers. Each firm plans the use of a grim trigger strategy to encourage compliance with the agreement. At what level of d would Honda be indifferent about keeping the agreement versus cheating on it? Explain.

Solution:
We can use the check method to solve for the Nash equilibrium in a one-
time game: 
The Nash equilibrium occurs when both firms offer a warranty. Note that this is not the best cooperative outcome for the game, but it is the only stable equilibrium.
485
If the game is played for three periods, there would be no change in the players’ behavior. In the third period, both firms would offer warranties because that is the Nash equilibrium. Knowing this and using backward induction, players will opt to offer warranties in both the second and the first periods as well.
Honda’s expected payoff from cheating and offering a warranty would be the 120 million from the first period (when cheating) and 20 million for each period after that (because Suzuki will also start offering warranties):
Expected payoff from cheating = 120 + d × (20) + d2 × (20) + d3 × (20) + . . .
Honda’s expected payoff from following the agreement is earning 50 million each period throughout time:
Expected payoff from following agreement = 50 + d × (50) + d2 × (50) + d3 × (50) + . . .
Therefore, Honda will be indifferent between these two options when the payoff streams are equal:
120 + d × (20) + d2 × (20) + d3 × (20) + . . . = 50 + d × (50) + d2 × (50) + d3 × (50) + . . .
d × (30) + d2 × (30) + d3 × (30) + . . . = 70
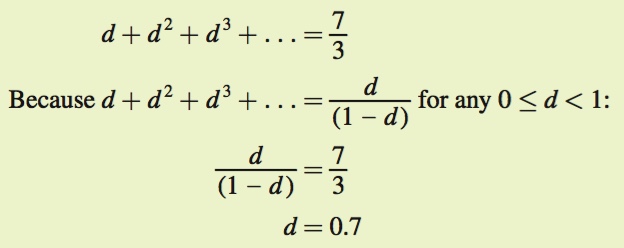
Therefore, Honda will be indifferent between following the agreement or cheating if d = 0.7.
Multiple Equilibria in Infinitely Repeated Games The weird thing about infinitely repeated games is that there are usually a whole range of possible Nash equilibria. Suppose Warner Brothers and Disney are playing tit-