Individual and Market Demand 5

5.2 How Price Changes Affect Consumption Choices

In the previous section, we looked at how changes in income affect a consumer’s choices, holding prices and preferences constant. In this section, we see what happens when the price of a good changes, holding income, preferences, and the prices of all other goods constant. This analysis tells us exactly where a demand curve comes from.

At this point, it is useful to recall exactly what a demand curve is. We learned in Chapter 2 that although many factors influence the quantity a consumer demands of a good, the demand curve isolates how one particular factor, the good’s own price, affects the quantity demanded while holding everything else constant. Changes in any other factor that influences the quantity demanded (such as income, preferences, or the prices of other goods) shift the demand curve.

Up to this point, it always seemed that demand curves slope downward because diminishing marginal utility implies that consumers’ willingness to pay falls as quantities rise. That explanation is still correct as a summary, but it skips a step. A consumer’s demand curve actually comes straight from the consumer’s utility maximization. A demand curve answers the following question: As the price of a good changes (while holding all else constant), how does the quantity of that good in the utility-maximizing bundle change? This is exactly the question we’re going to answer here.

Deriving a Demand Curve

To see how a consumer’s utility-maximizing behavior leads to a demand curve, let’s look at a specific example. Caroline is deciding how to spend her income on two goods, 2-liter bottles of Mountain Dew and 1-liter bottles of grape juice, and we want to know her demand curve for grape juice. Caroline’s income is $20, and the price of Mountain Dew is $2 per 2-liter bottle. We hold these other factors (income and price of Mountain Dew) and Caroline’s preferences constant throughout our analysis. If we didn’t, we would not be mapping out a single demand curve but would, instead, be shifting the demand curve around.

To build the demand curve, we start by figuring out the consumer’s utility-maximizing consumption bundle at some price for grape juice. It doesn’t actually matter what price we use to start because we will eventually compute the quantity demanded at all prices. Let’s start with a price of $1 per liter bottle of grape juice. (Because it makes the math easy.)

The top half of Figure 5.7 shows Caroline’s utility-maximization problem. Her budget constraint reflects the combinations of bottles of Mountain Dew and bottles of grape juice that she can afford at the current prices. With an income of $20, she can buy up to 10 bottles of Mountain Dew at $2 per bottle if that’s all she spends her money on, or up to 20 bottles of grape juice at $1 per bottle if she only buys grape juice. The slope of the budget constraint equals the negative of the price ratio P_G/P_MD, which is –0.5 in this case. The figure also shows the indifference curve that is tangent to this budget constraint. The point of tangency shown is the utility-maximizing bundle. Given her income, her preferences, and the prices of the two juices, Caroline’s optimal quantities to consume are 3 bottles of Mountain Dew and 14 bottles of grape juice.

Figure 5.8: Figure 5.7 Building an Individual’s Demand Curve

Figure 5.8: (a) At her optimal consumption bundle, Caroline purchases 14 bottles of grape juice when the price per bottle is $1 and her income is $20. The bottom panel plots this point on her demand curve, with the price of grape juice on the y-axis and the quantity of grape juice on the x-axis.

Figure 5.8: (b) A completed demand curve consists of many of these quantity-price points. Here, the optimal quantity of grape juice consumed is plotted for the prices $1, $2, and $4 per bottle. This creates Caroline’s demand curve, as shown in the bottom panel.

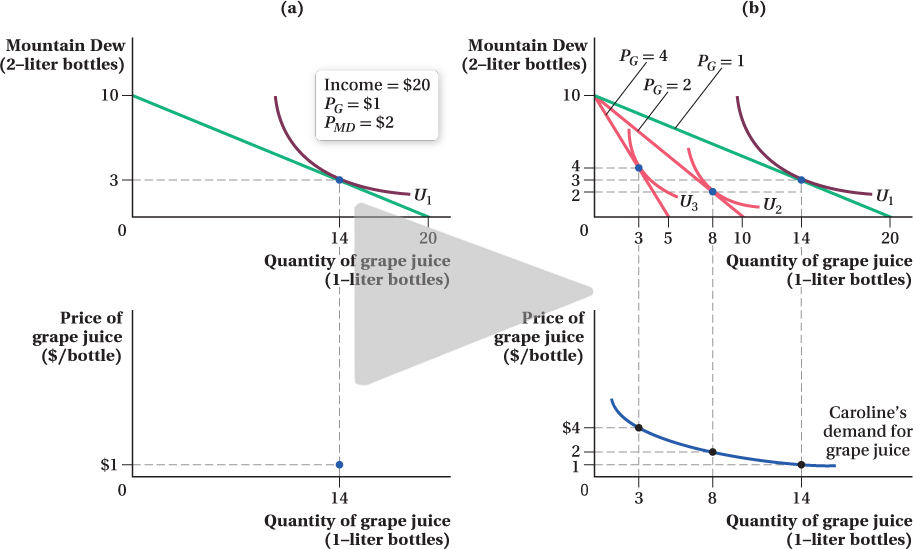
That is one point on Caroline’s demand curve for grape juice: At a price of $1 per liter, her quantity demanded is 14 bottles. The only problem is that the top panel of Figure 5.7a does not have the correct axes for a demand curve. Remember that a demand curve for a good is drawn with the good’s price on the vertical axis and its quantity demanded on the horizontal axis. When we graphically search for the tangency of indifference curves and budget constraints, however, we put the quantities of the two goods on the axes. So we’ll make a new figure, shown in the bottom panel of Figure 5.7a, that plots the same quantity of grape juice as the figure’s top panel, but with the price of grape juice on the vertical axis. Because the horizontal axis in the bottom panel is the same as that in the top—the quantity of grape juice—we can vertically transfer that dimension of the figure directly from the top to the bottom panel.

165

To finish building the demand curve, we need to repeat the process described above again and again for many different grape juice prices. When the price changes, the budget constraint’s slope changes, which reflects the relative prices of the two goods. For each new budget constraint, we find the optimal consumption bundle by finding the indifference curve that is tangent to it. Preferences are constant, so the set of indifference curves corresponding to Caroline’s utility function remains the same. The particular indifference curve that is tangent to the budget constraint will depend on where the constraint is, however. Each time we determine the optimal quantity consumed at a given price of grape juice, we identify another point on the demand curve.

Figure 5.7b shows this exercise for grape juice prices of $1, $2, and $4 per bottle. As the price of grape juice rises (holding fixed the price of Mountain Dew and Caroline’s income), the budget constraint gets steeper, and the utility-maximizing quantity of grape juice falls. In our example, Caroline’s optimal quantity of grape juice when it costs $2 per bottle is 8 bottles. When the price is $4, she consumes 3 bottles. These combinations of prices and quantities are plotted in the lower panel. These points are all on Caroline’s demand curve for grape juice. Repeating this exercise for every possible grape juice price will trace out her whole demand curve, which we’ve drawn in the figure. Caroline’s quantity demanded falls as price rises.

166

Shifts in the Demand Curve

We know that if a consumer’s preferences or income change, or the prices of other goods change, then the demand curve shifts. We can see how by tracing out the demand curve under these new conditions.

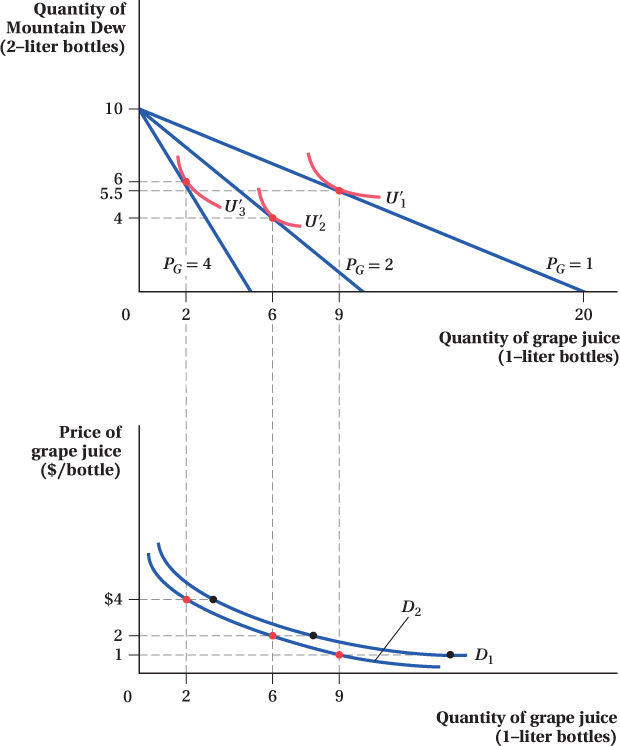
Let’s look at an example where preferences change. Suppose that Caroline meets a scientist at a party who argues that the purported health benefits of grape juice are overstated and that it stains your teeth red. This changes Caroline’s preferences toward grape juice, so that she finds it less desirable than before. This change shows up as a flattening of Caroline’s indifference curves, because now she has to be given more grape juice to be indifferent to a loss of Mountain Dew. Another way to think about it is that, because the marginal rate of substitution (MRS) equals –MU_G/MU_MD, this preference shift shrinks Caroline’s marginal utility of grape juice at any quantity, reducing her MRS—that is, flattening her indifference curves.

Figure 5.8 repeats the demand-curve building exercise after the preference change. With the flatter indifference curves (labeled U₁′, U₂′, and U₃′), Caroline’s utility-maximizing consumption bundles have changed. Now her optimal consumption levels of grape juice at prices of $1, $2, and $4 per bottle are 9, 6, and 2 bottles, respectively. The bottom half of Figure 5.8 plots these points on Caroline’s new demand curve D₂.

Figure 5.9: Figure 5.8 Preference Changes and Shifts in the Demand Curve

Figure 5.9: (a) Caroline’s indifference curves for grape juice flatten when her preference for grape juice decreases relative to her preference for Mountain Dew. At each price level, she now consumes fewer bottles of grape juice.

Figure 5.9: (b) Because she purchases fewer bottles of grape juice at each price point, Caroline’s demand curve for grape juice shifts inward from D₁ to D₂.

167

FREAKONOMICS

Even Animals Like Sales

If you think the laws of economics only apply to humans, think again. Monkeys, and even rats, behave in ways that would make you think they’ve taken intermediate micro.

Some of the most intensive testing of the economic behavior of animals was carried out by Yale economist Keith Chen and his co-authors on a group of Capuchin monkeys. As a first step, Chen introduced the monkeys to the concept of money. He gave them “money” in the form of metal washers that they could exchange for various types of foods including Jell-O, grapes, and Marshmallow Fluff (Capuchin monkeys love sweet foods).

Just Like Us?

M. Keith Chen

After about six exasperating months, these monkeys finally figured out that the washers had value. Chen observed that individual monkeys tended to have stable preferences: Some liked grapes the best, others were fans of Jell-O. How did he learn this? He would give a particular monkey a coin and then offer that monkey a choice between a bowl of three Jell-O cubes and a bowl of six grapes and see which one the monkey chose.

*Tim Harford, The Logic of Life: The Rational Economics of an Irrational World. (New York: Random House, 2008), pp. 18 – 21.

Next, Chen did what any good economist would do: He subjected the monkeys to price changes! Instead of getting three Jell-O cubes for one washer, he would offer the monkey, say, the choice between a single Jell-O cube per washer and a bowl of six grapes per washer. Thus, the relative price of Jell-O became three times as high. The monkeys responded exactly the way economic theory would predict, shifting their consumption away from the goods whose prices had risen.*

^* That wasn’t the only humanlike behavior these monkeys exhibited when exposed to money—for the whole amusingly sordid story, see the epilogue to SuperFreakonomics.

Perhaps it is not that surprising that monkeys, one of our closest relatives in the animal kingdom, would be sophisticated consumers. But there is no way rats understand supply and demand, is there? It seems they do. Economists Raymond Battalio and John Kagel equipped rats’ cages with two levers, each of which dispensed a different beverage.^† One of these levers gave the rat a refreshing burst of root beer. Rats, it turns out, love root beer. The other lever released quinine water. Quinine is a bitter-tasting substance initially used to treat malaria, and now used primarily to give vodka tonics their distinctive flavor. Rats are far less fond of quinine than they are of root beer, and they made that quite clear to the researchers by pressing the root beer lever far more often. Battalio and Kagel, like Chen, then explored changes in “prices” (how much liquid came out per press of the lever) and in the rats’ budget constraint (how many times they could press the levers each day). Like monkeys (and humans), the rats consumed less of a drink when its relative price increased. Even more interesting is that when the rats were made very poor (i.e., they got very few lever presses each day), they shifted their consumption away from root beer toward quinine water. The researchers found that root beer is a luxury good for rats, and quinine water is an inferior good! Perhaps if the researchers had only mixed the quinine with a little bit of vodka, things would have been different. . . .

^† A description of the work by Battalio and Kagel may be found in Tim Harford, The Logic of Life: The Rational Economics of an Irrational World (New York: Random House, 2008), pp. 18–21.

168

We can see that because Caroline’s preferences have changed, she now demands a smaller quantity of grape juice than before at every price. As a result, her demand curve for grape juice has shifted in from D₁ to D₂. This result demonstrates why and how preference changes shift the demand curve. Changes in Caroline’s income or in the price of Mountain Dew also shift her demand curve. (We saw earlier how income shifts affect quantity demanded, and we investigate the effects of price changes in other goods in Section 5.4.) Remember, however, that for any given value of these nonprice influences on demand, the change in the quantity demanded of a good in response to changes in its own price results in a movement along a demand curve, not a shift in the curve.

∂ The online appendix derives the demand curve directly from the utility function.

figure it out 5.2

Cooper allocates $200 of his weekly budget to entertainment. He spends all of this $200 on two goods: theater tickets (which cost $50 each) and movie tickets (which cost $10 each).

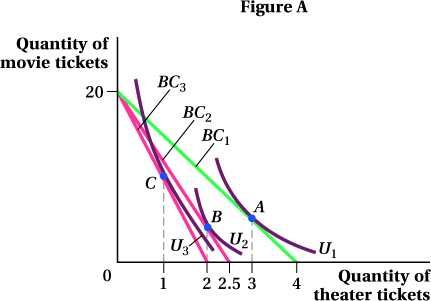
With theater tickets on the horizontal axis, draw Cooper’s budget constraint, making sure to indicate the horizontal and vertical intercepts. What is the slope of the budget constraint?
Suppose that Cooper currently purchases 3 theater tickets per week. Indicate this choice on the budget constraint and mark it as point A. Draw an indifference curve tangent to the budget constraint at point A. How many movie tickets does Cooper buy?
Suppose that the price of a theater ticket rises to $80, and Cooper lowers his purchases of theater tickets to 2. Draw Cooper’s new budget constraint, indicate his choice with a point B, and draw an indifference curve tangent to the new budget constraint at point B.
Once again, the price of a theater ticket rises to $100, and Cooper lowers his purchases of theater tickets to 1 per week. Draw his new budget constraint, show his choice on the budget constraint with a point C, and draw an indifference curve tangent to this new budget constraint at C.
Draw a new diagram below your indifference curve diagram. Use your answers to parts (b)–(d) to draw Cooper’s demand for theater tickets. Indicate his quantities demanded at $50, $80, and $100. Is there an inverse relationship between price and quantity demanded?

Solution:

To start, we need to calculate the horizontal and vertical intercepts for Cooper’s budget constraint. The horizontal intercept is the point at which Cooper spends all of his income on theater tickets and purchases no movie tickets. This occurs when he buys $200/$50 = 4 theater tickets (Figure A). The vertical intercept is the point at which Cooper spends his entire income on movie tickets and buys no theater tickets. This means that he is buying $200/$10 = 20 movie tickets. The budget constraint connects these two intercepts. The slope of the budget constraint equals rise/run = –20/4 = –5.

Note that this slope is the negative of the ratio of the two prices .
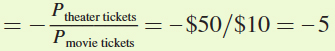Maximum utility occurs where the indifference curve is tangent to the budget constraint. Therefore, point A should be the point where this tangency takes place. If Cooper purchases 3 theater tickets a week, he will spend $50 × 3 = $150, leaving him $200 – $150 = $50 to spend on movie tickets. Since movie tickets cost $10 each, he purchases $50/$10 = 5 movie tickets.
Cooper’s budget constraint will rotate in a clockwise direction. The vertical intercept is not affected because neither Cooper’s income nor the price of movie tickets changes. However, the price of theater tickets has risen to $80, and now if Cooper were to allocate his entire budget to theater tickets, he could afford only $200/$80 = 2.5 of them. This is the new horizontal intercept. If Cooper chooses to buy 2 theater tickets, he will have an indifference curve tangent to this budget constraint at that point (B).
The budget constraint will again rotate clockwise and the vertical intercept will remain unchanged. The new horizontal intercept will be $200/$100 = 2. Point C will occur where Cooper’s indifference curve is tangent to his new budget constraint at a quantity of 1 theater ticket.
The demand curve shows the relationship between the price of theater tickets and Cooper’s quantity demanded. We can take the information from our indifference curve diagram to develop three points on Cooper’s demand curve:

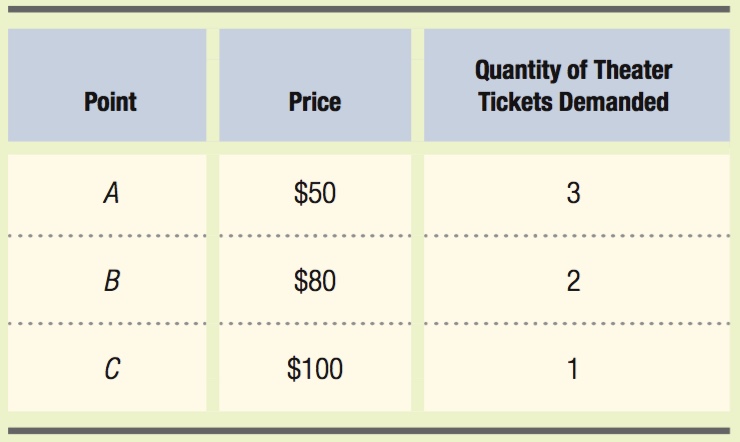
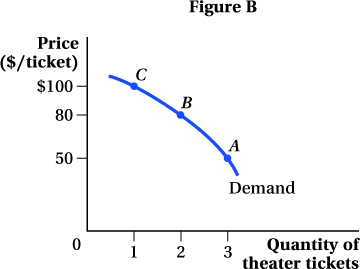
We can then plot points A, B, and C on a diagram with the quantity of theater tickets on the horizontal axis and the price of theater tickets on the vertical axis (Figure B). Connecting these points gives us Cooper’s demand curve for theater tickets.

169