Marginal Revenue
We know that all firms maximize profits when marginal revenue equals marginal cost. But what exactly is the marginal revenue of a firm? As we did in the past two chapters, we want to derive the relationship between marginal revenue and price. We’ll do this first for firms in general and then look specifically at the case of a perfectly competitive firm.
We will start with the expression for total revenue:
TR = PQ
Note that, in general, price P is not fixed, but is instead a function of the quantity the firm produces.11 To find marginal revenue, we take the derivative of the total revenue function with respect to Q using the product rule:
11The one exception to the general rule that price is a function of output that we’ve seen so far is for firms in a perfectly competitive market—
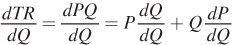
373
Equivalently,
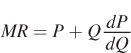
What does this tell us about the relationship between marginal revenue and price? Because a firm with market power faces a downward-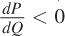
. Therefore, for a firm with market power,
MR < P
We can also see this result logically. P is the gain from selling an additional unit of the good at the new price.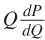 
is the loss from lowering the price on all previous units in order to sell the increased quantity. Therefore, the revenue from selling an additional unit of the good is less than the good’s market price, because for every gain in revenue (P), there is a corresponding loss 
.
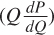Let’s work through a generic example to clarify this. Suppose a firm has the inverse demand curve P = a – bQ. (We discussed this particular inverse demand curve in footnote 3 in Chapter 9, but we’ll go into more detail here.) To find marginal revenue, we first determine total revenue by multiplying P by Q:
TR = PQ = (a – bQ)Q = aQ – bQ2
Now, we can take the derivative of total revenue to get marginal revenue:
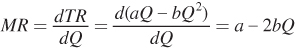
As you can see, the marginal revenue curve derived from a linear demand curve is itself linear. It also has the same price intercept (in this case, a) and is twice as steep as the demand curve. As a result, it’s clear that
a - 2bQ < a - bQ or
MR < P
But what about the special case of the perfectly competitive firm? Unlike firms with market power, perfectly competitive firms are price takers that face horizontal demand curves. We know from above that the marginal revenue for any firm is
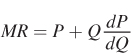
For a perfectly competitive firm, price remains fixed with changes in quantity, meaning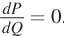 
Thus, MR = P for all quantities of output.
Therefore, the profit-
MR = P = MC
This unique relationship is precisely what we showed in Chapter 8.13
13We can also show the relationship between price, marginal revenue, and marginal cost for the perfectly competitive firm by starting from profit maximization. For the perfectly competitive firm, π = PQ – TC. Taking the first-
374
figure it out 9A.1
Let’s reconsider the solution to Figure It Out 9.2 and use the calculus approach we learned there. Babe’s Bats (BB) faces a demand curve of Q = 10 – 0.4P and a total cost curve of TC = 2.5Q2. BB’s output, Q, is measured in thousands of baseball bats, and P in dollars per bat.
Solve for BB’s profit-
maximizing level of output using calculus. What price will BB charge to maximize its profit?
Solution:
First, we need to set up Babe’s profit-
maximization problem: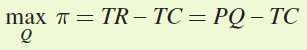 
Because Babe’s Bats has some market power, its choice of Q affects the price. So, we need to use the demand curve for BB’s bats to solve for price as a function of quantity, or the firm’s inverse demand curve:
Q = 10 – 0.4P
0.4P = 10 – Q
P = 25 – 2.5Q
Substituting this expression for P and the total cost curve into the profit function, we find
π = TR – TC = PQ – TC
= (25 – 2.5Q)Q – 2.5Q2
= 25Q – 2.5Q2 – 2.5Q2 = 25Q – 5Q2
So, the firm’s profit-
maximization problem is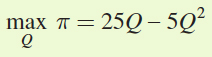 
The first-
order condition for this problem is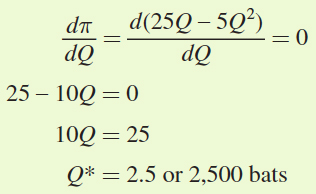 
Now we need to plug Q* from (a) into the inverse demand curve to obtain the profit-
maximizing price: P* = 25 – 2.5Q* = 25 – 2.5(2.5) = $18.75 per bat
Babe’s Bats is maximizing its profit when it sells 2,500 baseball bats at a price of $18.75 per bat. A shortcut to solving is to begin with the profit-
maximizing condition MR = MC, as we did in the chapter. In general, beginning with the profit- maximizing condition is easiest for firms with linear demand curves and simple cost functions. However, some firms have more complicated demand curves and total cost functions. For these firms, solving the profit- maximization problem directly using calculus may save you some work.
Now that we’ve worked through the calculus of profit maximization for a firm with market power, let’s look at an example for a perfectly competitive firm.
figure it out 9A.2
Let’s return to Figure It Out 8.1 and to Bob’s Barbershop, the perfectly competitive firm with a daily total cost of TC = 0.5Q2. Assume that the market price of a haircut is $15.
How many haircuts should Bob give each day if he wants to maximize his profit?
If the firm maximizes profit, how much profit will it earn each day?
Solution:
Bob’s problem is to choose the quantity of haircuts that will maximize his profit or
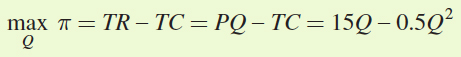
Solving for the first-
order condition gives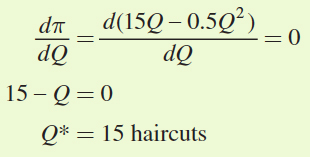 
Let’s confirm that this is the same result that we get from choosing the quantity where P = MC. In the chapter, the question provided you with the marginal cost, but now we can solve for it by taking the first derivative of the total cost curve with respect to quantity, the firm’s choice variable:
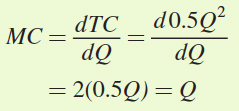
Now finding Bob’s optimal quantity of haircuts per day is easy:
P = MC
P = Q
Q* = 15 haircuts
At 15 haircuts per day, Bob will earn
π = TR – TC = PQ – 0.5Q2
= 15(15) – 0.5(15)2 = $225 – $112.50 = $112.50 per day
375