Problem Solving
A problem is a situation in which there is a goal, but it is not clear how to reach the goal. There are well-defined and ill-defined problems (Gilhooly, 1996). A well-defined problem is a problem with clear specifications of the start state (where you are), goal state (where you want to be), and the processes for reaching the goal state (how to get there). An ill-defined problem is a problem lacking clear specification of the start state, goal state, or the processes for reaching the goal state. Board games such as Monopoly and Scrabble represent well-defined problems. Their start states and goal states, along with the processes of moving from one to the other (the rules of the game), are all clearly specified. Getting your roommate to help clean the apartment would be an ill-defined problem. The start state and goal state are fairly well-defined, but the processes for moving between them are not. Most problems we confront are ill-defined, and to solve them we need to define the missing parts. We’ll see that blocks to solving problems may arise in this definition process.
Before learning about some of these obstacles to problem solving, I would like you to attempt to solve the following problems. You may recognize one of the series problems from Chapter 1. Don’t worry if you find these problems difficult; most people do. I will explain why.
- (a) Instructions: For each of these two series problems, your goal is to predict the next alphabetic character in each of the series. The answer to the first series is not “O.”
O T T F F S S ?
E O E R E X N ?
- (b) Instructions: Connect the nine circles using four straight lines without lifting your pen or pencil from the paper or retracing any of your lines. You should attempt this problem on a separate sheet of paper so that you can keep a record of your attempts. Once you have a four-straight-line solution, the next goal is to connect the nine circles with three straight lines using the same constraints as in the four-straight-line version.

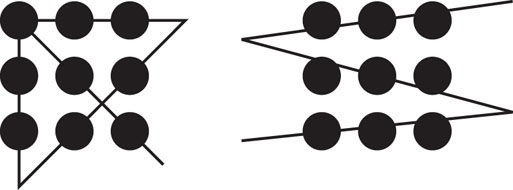
The sample four-straight-line solution is not unique. You may draw your first line from any of the other corner circles and continue from there to achieve a similar solution. The sample three-straight-line solution is taken from Adams (1986).
Blocks to Problem Solving
Problem solving can be divided into two general steps: (1) interpreting the problem and (2) trying to solve the problem. For many problems, the path to a solution is blocked in the first step by incorrectly interpreting the problem. This is like answering a test question too quickly, only to find out later that you misinterpreted the question. If you are working with such a misinterpretation, you will probably fail to solve the problem. The two nine-circle problems are good examples of problems that often lead to misinterpretations. Let’s see how.
Interpreting the problem.
Look at your failed attempts at solving the nine-circle problem involving four straight lines. Did you try to keep your lines within the mental square created by the circles? Most people do, and you cannot solve the problem this way (Wickelgren, 1974). Not only do most people create this misinterpretation, but they also continue to use it even though they make no progress toward solving the problem. This inability to “think outside the box” and create a new interpretation of a problem is called fixation. Reread the instructions. You were not required to keep your lines within this mental square. Any or all of the four lines can extend outside this space. The lines only have to be straight and connect all nine circles. Knowing this, try again to solve the problem. Draw a straight line that goes down through the first column of circles and continues on outside of the mental square. When you bring your next line back up, also continue it outside of the mental square. This should start you on your way to a solution, though it may still be elusive (Weisberg & Alba, 1981).

231
What about the second nine-circle problem—connecting all nine circles with three straight lines? If you didn’t solve it, think about the assumptions that you made when you interpreted the problem. This problem is even more difficult, because you may have made two mistakes in your interpretation and fixated on them, making the problem impossible to solve. First, as in the four-straight-line problem, you might have assumed that you need to keep your lines within the mental square created by the circles. Second, you might have assumed that the lines need to go through the centers of the circles. Neither assumption is valid. Now try to solve this problem knowing that both of these assumptions are misinterpretations. Try drawing three straight lines that do not go through the centers of the circles and that travel outside the mental square. It might help to imagine using a very long ruler to draw your lines. If you’re still stumped on either one of these problems, look at the sample solutions at the end of the chapter.
Another obstacle to problem solving is functional fixedness—the inability to see that an object can have a function other than its typical one. This type of fixation also occurs during the problem definition stage. Functional fixedness limits our ability to solve problems that require using an object in a novel way (Duncker, 1945). This often happens to us in our everyday life. Maybe we need a screwdriver, but one isn’t available. We have other things such as coins that could function as a screwdriver, but we may not think about using them in this novel way. Or, what if you just did some grocery shopping, and as you are about to walk out of the store it starts raining hard. You have no umbrella. How can you avoid getting soaked? You bought some large trash bags, but you may not think about using one as a raincoat to protect you from the rain. To combat functional fixedness, we should systematically think about the possible, novel uses of all the various objects in the problem environment. This is bound to increase our ability to solve the continual problems that come up in our daily lives.
Solving the problem.
Problem misinterpretation and functional fixedness are good examples of the negative impact that our past experiences can have on our ability to solve current problems. Our past experience with problem solving can also lead to a phenomenon known as mental set—the tendency to use previously successful solution strategies without considering others that are more appropriate for the current problem. Mental set is especially common for strategies that have been used recently. Consider the two letter-series problems. If you had difficulty solving them, mental set may be what hindered you (Griggs, 2003). You probably attempted to solve these two problems with strategies that you have used successfully in the past with series problems. You may have viewed the letters in the series as single entities and looked for relationships between them. This strategy does not include viewing each of the letters as part of some larger entity. You cannot solve the series unless you do so. For the first series problem, you should think of the letters as the first letters in the words of a well-known ordering. It’s as easy as 1-2-3.
232
The solution: These are the first letters in the sequence of number words—One, Two, Three, Four, Five, Six, Seven—so the answer is E for Eight. This should help you to solve the second series problem, but don’t fall prey to mental set and try to find another well-known ordering in which these are the first letters of the words in the sequence. You need to look for another solution strategy. Because of mental set, you probably don’t see the strategy, but it’s directly related to the solution to the first series. The letters in the second series are the last letters in the number words—onE, twO, threE, up to seveN. The answer is T for eighT. What’s the lesson to be learned? Don’t cling to solution strategies that have worked in the past, but which are not presently working. Try new approaches.
Sometimes when searching for new approaches to a problem, we may experience what has been called insight—a new way to interpret a problem that immediately gives the solution. This rapid understanding is the key to the solution. Insight is sometimes referred to as an “Aha!” or “Eureka!” experience. Try the following problem from Knoblich and Oellinger (2006). You may experience insight in solving it. The solution is given below.
- Instructions: The equation shown is not correct. To create a correct equation, you can move only one matchstick (but not remove it). Only Roman numerals and the three operators, +, −, and = are allowed.
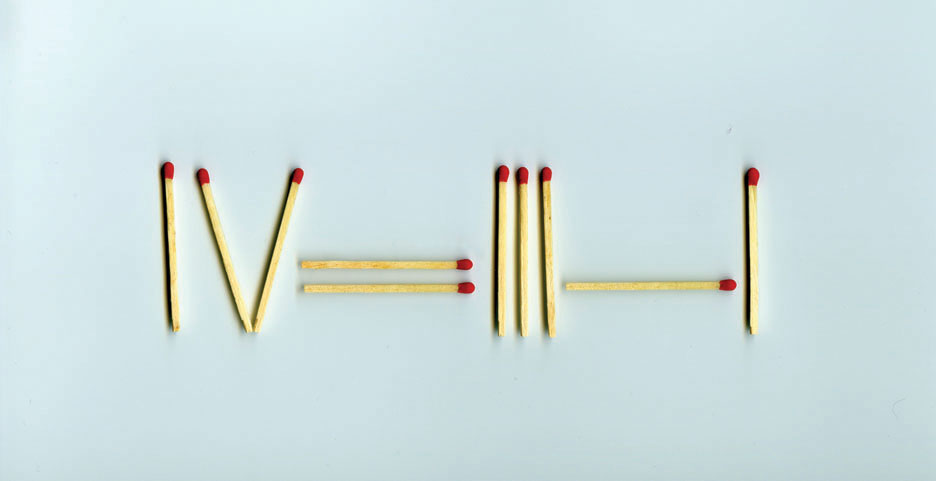
As Knoblich and Oellinger (2006) explain, most people try to create a correct equation by moving a matchstick that changes the numbers because we are taught in school that solving math problems is all about manipulating quantities. This knowledge, however, blinds us to the needed insight. To experience insight on this problem, you need to change your perspective about where the solution might lie—realize that you can also change operators. The solution lies in moving one matchstick to change the operators as shown below.

For insight problem solving tasks such as matchstick problems, the frontal cortex (home to executive processes such as planning, judging, evaluating, and deciding) may actually hinder insight rather than facilitate it (Restak & Kim, 2010). Reverberi, Toraldo, D’Agostini, and Skrap (2005) found that patients with damage to their lateral frontal cortex actually outperformed healthy participants on insight problems. While only 43 percent of healthy participants could solve some very difficult matchstick problems, 82 percent of patients with frontal lobe damage did so. Thus, our intact frontal lobes may lock us into less than optimal solution strategies (a mental set effect) for insight problems. In the Reverberi et al. study, the patients with frontal lobe damage were freed from this constraint and were more successful in solving the problems, indicating that other brain regions may be more critical to solving insight problems.
Recent research indicates that the right anterior temporal lobe (directly above the right ear) may be such a region. Chi and Snyder (2011) found that noninvasive transcranial direct current stimulation of the anterior temporal lobes (inhibiting the left anterior temporal lobe and activating the right anterior temporal lobe) facilitated the solution of insight problems. The stimulation led to a threefold increase in solving difficult matchstick problems. Hence, maybe the advice to “think outside the box” should be amended to be “think outside the frontal lobes.” Chi and Snyder (2012) also found that this same transcranial stimulation of the anterior temporal lobes will facilitate the solution of the nine-circle problem. None of the participants solved the problem before stimulation; 14 of 33 broke fixation and solved it as a result of receiving the stimulation. Chi and Snyder calculated that the probability that this fraction of the participants could solve it by chance is less than one in a billion.
233
You might wonder if there is any validity to prescriptive advice such as to “think outside the box.” Metaphors such as this (and others such as to consider a problem “on one hand and then on the other”) suggest a connection between concrete bodily experiences and creative problem solving in which physically enacting the metaphor would enhance creative problem solving. Leung et al. (2012) have provided the first evidence that such embodiment might activate cognitive processes that facilitate creativity. For example, subjects trying to solve an innovative verbal thinking task performed much better if they sat and thought outside rather than inside a 125-cubic-foot box made of plastic pipe and cardboard. Similar results were observed for another creativity task for subjects solving the task while walking freely outside a fixed rectangular path indicated by duct tape on the floor (marking out a box of about 48 square feet in area) versus walking along the path. Obviously much more research is needed on this experimental question, but these initial findings indicate that thinking “outside the box” may not be a cliché; you might just need to use an actual box.
We have discussed many potential blocks to problem solving, and it takes a very conscious, concerted effort to overcome them. What can you do? Ask yourself questions such as the following: Is my interpretation of the problem unnecessarily constraining? Can I use any of the objects in the problem in novel ways to solve the problem? Do I need a new type of solution strategy? If we do not make this effort, we are engaged in what is called mindless behavior—rigid, habitual behavior in which we fail to attend carefully to the details of the present situation (Langer, 1989, 1997). To be good problem solvers, we will need to be open to new interpretations of problems and to new ways of using objects to solve problems. We will also need to develop a broader, more effective set of solution strategies, which is our next topic.
Solution Strategies
Just as problem solving can be divided into two steps, solution strategies can be divided into two types—algorithms and heuristics. An algorithm is a step-by-step procedure that guarantees a correct answer to a problem. For example, when we solve a math problem with long division, we are using an algorithm. If we execute the steps correctly, we will get the correct answer. For many problems, however, we may not know the algorithm or an algorithm for the problem may not exist. To solve the problem in such cases, we have to use a heuristic, a solution strategy that seems reasonable given our past experiences with solving problems, especially similar problems. Think of a heuristic as an educated guess.
234
Sometimes you may even know the algorithm for a problem, but you don’t use it because its execution would be too time-consuming. Instead you may try some heuristics, and they might pay off with a quicker answer, or they may lead to no answer or an incorrect one. This is the crucial difference between an algorithm and a heuristic. An algorithm guarantees a correct answer (if it’s the correct algorithm for the problem and you execute it correctly), but a heuristic makes no guarantees. Let’s consider some problems (anagram word puzzles) for which you likely know the algorithm, but because it would usually be too difficult to execute, you use heuristics instead. In an anagram puzzle, the letters of a word are presented in a scrambled order, and the problem is to rearrange them to determine the word. Now, what’s the algorithm for such puzzles? Generate each possible sequence of the letters and check to see if each sequence is a word. This sounds simple, but it isn’t. For example, there are over 5,000 possible sequences of the letters for a seven-letter anagram! So unless there are only a few letters in the anagram, we use heuristics based upon our knowledge of the English language. For example, we know that the letter U usually follows the letter Q and that certain letters such as B and C don’t follow one another in words. We attempt to create words with the letters following such principles. To understand this strategy, let’s work a couple of anagram puzzles. As you try to solve them, think about the strategy you are using.
- Instructions: Rearrange the letters in each anagram puzzle to form a meaningful word in the English language.
- 1. L O S O G C Y H Y P 2. T E R A L B A Y
The first puzzle is rather easy. The answer is especially relevant to this text. It’s PSYCHOLOGY. Your use of heuristics was probably successful and led to a quick answer. The second puzzle is more difficult. Your use of heuristics may have failed and didn’t yield a solution. Even so, you probably didn’t switch to using the algorithm. You probably kept trying to find a solution by using heuristics. As you can see, heuristics might pay off with quick answers, but they may lead to no answer as in the second anagram puzzle. Now think about the algorithmic strategy. There are over 40,000 sequences for the eight letters in the second anagram puzzle; therefore, generating each of them to check if it’s a word would take far more time and effort than we are willing to spend. However, if you did so, you would find that the answer is BETRAYAL.
Now let’s consider three particular heuristics that are used fairly often in problem solving—the anchoring and adjustment, working backward, and means–end analysis heuristics. We’ll start with the anchoring and adjustment heuristic.
Anchoring and adjustment.
To help you to understand this heuristic, let’s try an estimation problem taken from Plous (1993). The task involved in this problem would be impossible to execute. It is only a hypothetical problem that examines how we make estimates.
235
- Estimate how thick a sheet of paper that is 0.1 millimeter thick would be if it were folded in on itself 100 times.
Most people estimate the thickness to be only a few yards or so, which is not even close to the correct answer: 0.1 millimeter × 2100, which equals 800 trillion times the distance between the earth and the sun (Plous, 1993)! Why do we underestimate this thickness by so much? We are most likely using the anchoring and adjustment heuristic in which an initial estimate is used as an anchor and then this anchor is adjusted up or down. The difficulty in using the anchoring and adjustment heuristic is that we tend to attach too much importance to the starting anchor amount and do not adjust it sufficiently (Tversky & Kahneman, 1974). The folding problem is a good illustration of this bias. If you double the thickness of the sheet of paper a few times, you still have a rather small thickness. Using this small thickness as an anchor for making your estimate, you do not adjust the estimate sufficiently and usually guess only a few yards. In this case, the anchoring and adjustment heuristic leads us to ignore the fact that the powers of 2 grow exponentially as we double them and become very large very quickly.
This estimation problem was only a hypothetical exercise, but it shows how we fail to adjust the anchor enough when using the anchoring and adjustment heuristic. Anchoring is a very robust psychological phenomenon and has even been shown to hold when the anchors represent the same physical quantity, 7.3 kilometers and 7,300 meters (Wong & Kwong, 2000). Estimates for the 7.3 km group were much lower than those for the 7,300 m group. Anchoring has been shown to influence judgments in a variety of domains such as making judgments in personal injury cases (Chapman & Bornstein, 1996), negotiating (Ritov, 1996), and playing the stock market (Paulos, 2003). In the real world, anchoring may have costs attached to it. A good example that you may have experienced is the inclusion of minimum payment information on credit card statements. These minimum payment amounts can act as psychological anchors (Stewart, 2009; Thaler & Sunstein, 2008). In a hypothetical bill-paying experiment manipulating the inclusion of minimum payment information, Stewart (2009) found that the inclusion of this information led to significant reductions in partial payment amounts, which in the real world would lead to increased interest charges. We should also beware of using this heuristic when meeting people. Our first impression of a person is similar to forming an anchor. We must be sure to process subsequent information about the person carefully and adjust our impression (anchor) sufficiently. Remember, the anchoring and adjustment heuristic leads us to fail to adjust the anchor enough. So do not become too attached to an anchor when making judgments and decisions.
236
Working backward.
Working backward is a heuristic that you may have learned to use in your math classes. The working backward heuristic is attempting to solve a problem by working from the goal state backward to the start state (Wickelgren, 1974). In math problems, this translates to working backward from the answer to the given information in the problem. To see how this heuristic would work, consider the following problem (Sternberg & Davidson, 1982):
- Water lilies growing in a pond double in area every 24 hours. On the first day of spring, only one lily pad is on the surface of the pond. Sixty days later, the pond is entirely covered. On what day is the pond half covered?
Did you solve it? It is impossible to solve this problem working in a forward direction. However, if you work backward by starting with the fact that the pond is entirely covered on the sixtieth day, you can solve it rather easily. Just ask yourself how much of the pond would be covered on the fifty-ninth day if the pond were entirely covered on the sixtieth day. The answer is half. The working backward heuristic is ideal for problems that have many possible paths from the start state, but only one path (or a few) going backward from the goal state.
Means–end analysis.
A good heuristic for working forward on a problem is means–ends analysis. In the means-end analysis heuristic, the problem is broken down into subgoals and we work toward decreasing the distance to the goal state by achieving these subgoals. Consider the following Tower of Hanoi problem. It is a well-defined problem. The start state, the goal state, and the rules for moving from the start state to the goal state are all clearly specified.
Instructions: The problem is to create the same configuration of disks on Peg C as is on Peg A in the starting state. Rules, however, govern your moves. You can only move one disk at a time, and you cannot place a larger disk on top of a smaller disk. Try to solve this problem efficiently by minimizing the number of moves that have to be made. The most efficient solution involves seven moves.
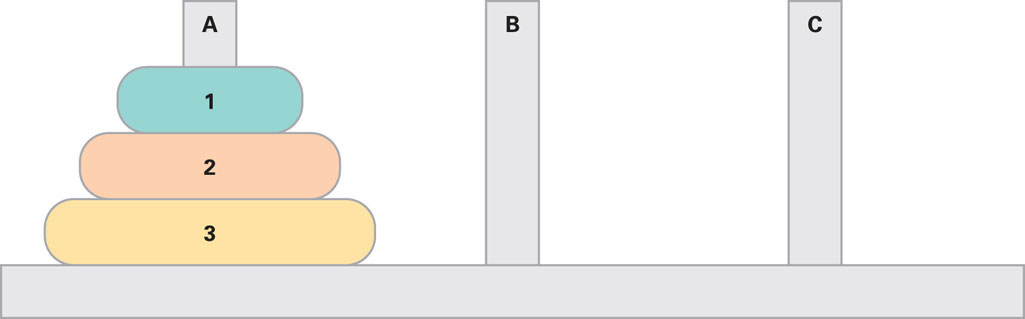
Move 1: Move Disk 1 to Peg C
Move 2: Move Disk 2 to Peg B
Move 3: Move Disk 1 to Peg B
Move 4: Move Disk 3 to Peg C
Move 5: Move Disk 1 to Peg A
Move 6: Move Disk 2 to Peg C
Move 7: Move Disk 1 to Peg C
Let’s try to use means–end analysis to solve the problem. What would be the first subgoal? You have to get Disk 3 on Peg C. You cannot, however, achieve this immediately, so you have to set up another subgoal. What is it? You have to get Disk 1 on top of Disk 2 on Peg B. You cannot achieve this immediately either, so what is the next subgoal? Yes, you have to get Disk 2 on Peg B. To achieve this, you need to get Disk 1 off Disk 2 and not on Peg B. How do you achieve this subgoal? By now you should have the idea. Go ahead and finish solving the problem. It takes a minimum of seven moves. (The list of moves is given at the end of this chapter.) Using means–end analysis (setting up subgoals and so on) to solve the Tower of Hanoi problem obviously involves planning. Remember that Phineas Gage’s left frontal lobe damage led to deficits in planning. Thus, patients with frontal lobe damage should have difficulty solving this problem, and this is exactly what Goel and Grafman (1995) and Morris, Miotto, Feigenbaum, Bullock, & Polkey (1997) found.
237
The specific solution steps to a Tower of Hanoi problem with a certain number of disks can be varied by manipulating the start and goal states (which peg the disks are on and which peg they need to be moved to, respectively). Such changes allow researchers to see if problem performance is enhanced with practice on various versions of the problem. As you would expect, they found that people do get more efficient in solving these problems with practice. Interestingly though, this practice effect is also shown by anterograde amnesics, such as H. M. (who was described in Chapter 5). They too can learn to solve the Tower of Hanoi problem (their frontal lobes are intact) and solve it more efficiently with practice, but they have no recollection each time of ever having seen the problem before (Squire & Cohen, 1984). Why? As we learned in Chapter 5, amnesics like H. M. form implicit procedural memories from practice in solving a problem because their cerebellum and basal ganglia are intact, but no explicit episodic memories of working on the problem are formed because the hippocampus is critical for forming such memories and they have had their hippocampus removed.
Given the solution to the 3-disk Tower of Hanoi problem described above, let’s consider a 64-disk Tower of Hanoi problem. Everything is the same except the number of disks—64 instead of 3. What is your estimate of the minimum number of moves necessary to solve the 64-disk version? Don’t read further until you derive an estimate. If you used the anchoring and adjustment heuristic to derive an estimate, you probably greatly underestimated the answer. You probably derived a rather small anchor based on the 3-disk version that required only seven moves and then failed to adjust it upward sufficiently. The minimum number of moves for the Tower of Hanoi problems is 2n − 1, where n is the number of disks (Raphael, 1976). Thus, for 3 disks, it is 7, or 23 − 1. Now do you see the problem with your estimate? The answer for 64 disks is 264 − 1, or trillions of moves! Did the anchoring and adjustment heuristic lead you astray again?
The events in our everyday lives are not as well-defined as the allowable moves in a Tower of Hanoi problem. They are uncertain. They have varying probabilities of occurring, and therefore we have to learn how to think in a probabilistic world. Such thinking involves estimating event probabilities (uncertainties). The heuristics we have discussed so far are not usable for this type of judgment. The heuristics that we do use to make these probability judgments and, more generally, how we think under uncertainty are the main topics of the next section.
238
Section Summary
In this section, we discussed how problems are either well-defined or ill-defined. Well-defined problems provide clear definitions of the start and goal states, and the processes for reaching the goal state from the start state. Ill-defined problems do not. Everyday problems tend to be ill-defined; therefore, interpreting the problem is necessary. Such interpretation may block problem solving. Blocks can be caused by problem misinterpretation, functional fixedness, or mental set. These blocks are all examples of the negative impact of our past experience on problem solving. We must make a mindful effort to overcome these blocks or our problem solving will suffer.
When attempting to solve a problem, we use either an algorithm that guarantees us a correct answer or heuristics that may lead to a quick solution or possibly to no solution. We prefer to use heuristics because they are less time-consuming. In addition, we may not know the appropriate algorithm for a problem or one may not even exist. Sometimes heuristics can lead to errors. A good example is the anchoring and adjustment heuristic for making estimates. The error in this case stems from our failure to adjust our initial anchor sufficiently.
The working backward heuristic is especially useful for problems that have many paths going forward from the start state but only one (or a few) going backward from the goal state. Means–ends analysis is a useful heuristic for almost any type of problem. In this heuristic, you move forward by achieving subgoals that continue to reduce the distance between the start state and goal state.
ConceptCheck | 1
 Explain how functional fixedness and mental set are examples of the negative impact of past experience.
Explain how functional fixedness and mental set are examples of the negative impact of past experience.In functional fixedness, we fixate on the normal function of an object given our past experiences with that object. Our past experience with the object may block us from seeing how to use it in a novel way. Similarly, mental set leads us to approach a problem in the same way we have approached similar problems in the past, especially the recent past. We tend to block developing a new approach because our mental set keeps us locked into the old approach based on our past experiences.
 Explain why we tend to use heuristics and not algorithms even though algorithms guarantee correct solutions.
Explain why we tend to use heuristics and not algorithms even though algorithms guarantee correct solutions.We use heuristics rather than algorithms because algorithms tend to be timeconsuming and more difficult to use. Solving anagram puzzles is a good example of a case where we know the algorithm, but we do not use it unless there are only a few letters, because it is too time-consuming and difficult to use.
 Explain how the anchoring and adjustment heuristic may lead you to make a serious error in estimation.
Explain how the anchoring and adjustment heuristic may lead you to make a serious error in estimation.The anchoring and adjustment heuristic leads to a serious error in estimation when we fail to adjust our initial anchor sufficiently either up or down in magnitude. The paper-folding problem is a good example of such a failure.