Chapter 1. Chemical Equilibrium and Thermodynamics

Movement is a defining characteristic of living systems. To move anything large or small takes work, which requires energy.

We need to learn how to study movement of energy and how energy produces movement.

Table of Contents

To understand thermodynamics, we need to introduce the concept of equilibrium

Learning Goals and Objectives

Goal: To understand why a cell is dead if it reaches equilibrium.

Objectives: You should be able to….

• Define K_eq, ΔG°_Rxn, and ΔG, and be able to relate these values to the spontaneity of a given chemical reaction.
• Draw, label and interpret diagrams showing the changes in Gibbs free energy as a function of the chemical composition of a given reaction mixture.
• Explain how Le Chatelier’s principle allows cells to perform unfavorable reactions.
• Define pH, pK_a, and K_a, and relate these values to one another. One should be able to explain and interpret the meaning of each parameter.
• Draw chemical structures showing the protonation state that would predominately exist at different pH values given the pK_a values of a molecule’s ionizable groups.

All Living Systems Require Energy

The cell is a very complex system and is not simply evolved from simple components. In the last lecture, we talked about the types of molecules in a cell and also the forces that hold these molecules together and we said that the molecules and forces that we see in a cell are in fact no different from those that are in a flask. So although it is necessary to understand molecules and forces to understand what makes a cell alive, it is not sufficient.

You all know that living systems require energy. If you stop eating, you will eventually stop living. It may take awhile because your body can live on stored fat and on excess muscle for weeks, but sooner or later you will die. You might wonder why a cell needs energy. Where does the energy come from and where does it go? Before we can answer that question, we need to introduce thermodynamics. Thermodynamics deals with the energy flow in any system. Thermodynamics helps us to predict how systems will behave under different sets of circumstances and whether a reaction will occur spontaneously—that is, without an input of energy.

The 1st Law of Themodynamics

You have probably all heard the first law of thermodynamics, which states that energy cannot be created or destroyed. It can only be converted from one form to another, or used to do work. When we add energy to solid water (ice) by heating (thermal energy), the first thing that happens is that the energy of the molecules within the solid ice increases and the molecules start to wiggle around more. The thermal energy is converted to kinetic energy (motion). As the heating continues, some water molecules gain enough energy to break away from the other water molecules. Since water molecules interact through hydrogen bonding, and we need energy to break those interactions, we can say that the water molecules are using the kinetic energy that they have gained to do work.

One of the hallmarks of a living system is that it can metabolize, i.e. make use of, food (carbohydrates, proteins, fats) as an energy source. One of the main things that occurs in metabolism is that glucose (C₆H₁₂O₆) combines with oxygen through multiple processes (including the glycolytic pathway, which is shown on this slide) to give carbon dioxide and water. As you will see in the next slide, energy is released when glucose and oxygen are converted to carbon dioxide and water. Some of the energy that is released by the transformation can be converted to other forms of energy. A key function of the glycolytic pathway (and later metabolic processes) is to convert the released energy to another energy store known as adenosine triphosphate (ATP—colored red in diagram) in the cell, which can later be used by cellular machinery to help carry out important reactions of metabolism. You will learn about ATP later in the course. (You do not need to know the details of the glycolytic pathway for this course).

Products of the Krebs Cycle reduce oxygen and produce ATP.

Cells Get Energy From Food

Cells need energy to make biomolecules to carry out cellular transformations. To get energy, cells burn fuel. One of the universal fuels used by all cells from bacteria to man is glucose. To burn any fuel requires oxygen. Oxygen reacts with glucose (or any fuel) to form carbon dioxide and water. The process by which this occurs in cells involves multiple steps. Those steps are not important. What is important is that the overall transformation involves the release of energy.

On this slide, glucose and oxygen are depicted as being at a higher energy level than carbon dioxide and water to capture the idea that there is a release of energy when this reaction occurs. We say that this reaction is energetically favorable or that it occurs “spontaneously”. (However, as you will learn, some spontaneous reactions are very fast while others occur at a glacially slow pace. We will introduce kinetics—the rates at which reactions occur—after thermodynamics. It is another concept that will be used throughout the course).

Some Reactions Release Energy But Other Reactions Require Energy

Some reactions release energy. Others require energy. The reaction of carbon dioxide and water to form glucose is not one that can occur spontaneously because it requires going from a lower energy state to a higher energy state.

That energy ultimately comes from the sun. We aren’t going to focus now on how the energy of the sun is harnessed to drive reactions towards disfavored (higher energy) products. Instead, we are going to ask how one can tell whether a reaction is favored or disfavored. Once we know that, we can begin to explain better how Nature accomplishes the impressive feat of driving reactions in either the favored or the disfavored directions depending on the immediate needs of the cell.

It Is Not Easy to Look at Starting Materials and Products and Know Which is Lower in Energy

How do we know which way is uphill in energy and which way is downhill in energy for a chemical reaction? Do we simply “measure” the amount of energy in the individual molecules by some means? The answer is NO. Energy itself is not a measurable entity, but other quantities related to energy are measurable. For example, in order to know how much kinetic energy (K.E.) a person has while running, we can measure the speed of the person and his or her mass. Then we can crudely (neglecting various complicating factors) calculate the K.E. that this person possesses using the relationship K.E. = 0.5mv². Similarly, to know the chemical energy in a system, we must use measurable observables that we can relate to energy. These observables include concentrations and temperature. In order to relate the measured observables to the energy in a system, we need to introduce the concept of chemical equilibrium.

To do that, we will consider a simple chemical reaction, the hydration of carbon dioxide. Carbon dioxide is taken in by plants and converted into glucose. An early step in the process of converting CO₂ to glucose, which is shown on the next slide, involves the reaction of carbon dioxide with water. We will use this reaction to understand the concept of chemical equilibrium.

What Does it Mean for Starting Materials and Products to be in Equilibrium?

This slide depicts two reactions. The first is one we talked about in earlier lectures. The second is the one I just introduced. Note that the reactions are drawn with two stackedarrows, one pointing to the left and the other pointing to the right. In the top reaction, the arrow pointing to the right represents the conversion of liquid water to gaseous water while the arrow pointing to the left represents the conversion of gaseous water to liquid water. In the bottom reaction, the arrow pointing to the right represents the addition of water to carbon dioxide to form carbonic acid while the arrow pointing to the left represents the decomposition of carbonic acid to form carbon dioxide and water. If these molecules are allowed to interconvert under a given set of conditions, they will reach a point where the concentrations of the interconverting species are stable. We say they have reached equilibrium; that is, the rate at which A is converted to B (i.e., the number of molecules in state A that are converted to state B per minute) is identical to the rate at which B is converted back to A. Although reactions occur in both directions, no net interconversion takes place.

We will use the example of hydration of carbon dioxide to further discuss chemical equilibrium and thermodynamics. This reaction is simple, but it also happens to be important. CO₂ is one of the greenhouse gases that contribute to global warming. That is, CO₂ produced by industrial activity (burning things to get energy) absorbs radiation reflected from the earth’s surface, trapping it in the atmosphere and warming the planet. A significant portion of the CO₂ that is formed is absorbed into the oceans where some of it combines with water to form carbonic acid. For a long time, people thought this was a good thing because it reduced the amount of CO₂ in the atmosphere. The problem is that the carbonic acid that is formed makes the water more acidic. That, in turn, causes all kinds of sea creatures—corals and lots of other things—that have calcium carbonate exoskeletons to dissolve. This is an example of something we call “Le Chatelier’s Principle,” which we will also talk about.

The Reaction of Carbon Dioxide and Water Could Be Bad for Life

In the reaction shown on this slide, the hydration of carbon dioxide, carbon dioxide (CO₂) and water (H₂O) exist in equilibrium with carbonic acid (H₂CO₃). CO₂ (aq.) refers to carbon dioxide in an aqueous environment. As depicted in the slide, carbon dioxide interacts with water through hydrogen bonding (a type of permanent dipole-permanent dipole interaction). The same is true for H₂CO₃ (aq.). The symbol (l) in the equation indicates that the water referred to here is in the liquid state. (aq.) and (l) are called state symbols and they are very important and should be included in equations when we are talking about equilibrium and thermodynamics. Other state symbols include (s) for solid, (g) for gas, etc.

You can see that when carbon dioxide is converted to carbonic acid, a C-O bond is formed between the C atom of carbon dioxide and the O atom of a water molecule. In the process, one of the C=O bonds (a double bond) in carbon dioxide becomes a C-O (a single bond). The C atom in the molecule still forms four bonds and maintains the octet configuration.

You might wonder: which side of the reaction shown above is favored?

The Equilibrium Constant (Keq) Reflects Which Side of the Reaction is Favored

To tell which side is favored, you measure the concentrations of the chemical species at equilibrium—that is, after the reaction has reached the point where the concentrations of the products and the reactants have stopped changing. All reactions have a characteristic equilibrium constant ,K_eq, under a given set of conditions. K_eq is defined as the ratio of the product of the concentrations of the species on the right (by convention, we refer to these as the products) over the product of the concentrations of the species on the left (by convention, we call these the reactants). That is, for a reaction A + B <==> C + D, K_eq = [products]/[reactants] = [C][D]/[A][B]. If K_eq is less than 1, then the concentrations of the products are lower than the concentrations of the reactants at equilibrium. Conversely, if K_eq is greater than 1, then the concentrations of products are greater than the concentrations of the reactants. If K_eq is exactly 1, then there is a fifty:fifty mixture of reactants and products at equilibrium.

In addition to the conditions given on the slide, there are two extremes of Keq that we can also consider. If K_eq ~ 0 (close to zero), it means that at equilibrium, there is almost no product. That is, the reaction does not proceed. If Ke_eq ~ ∞ (close to infinity), it means that at equilibrium, almost all the reactants will have become the products. In other words, the reaction has proceeded to completion.

For the hydration of carbon dioxide, the concentrations of the products and reactants have been measured. It is not important how, but it is straightforward. The concentration of water is so high compared to the other species that it is essentially constant and has the value of 55 M at atmospheric pressure. From the concentrations of the products and reactants, an equilibrium constant, K_eq, of 3.09 x 10^-5 M^-1 at 25°C has been measured. This means that the left side of the reaction is (strongly) favored, and when carbon dioxide is dissolved in water, only a small fraction of it is converted to carbonic acid at equilibrium.

The Position of a Chemical Equilibrium is Independent of the Initial State

This slide depicts what happens if you start out with very different concentrations or ratios of reactants and products. If you start out with a 100% solution of aqueous carbonic acid (H₂CO₃), you will observe that the concentration of H₂CO₃ decreases with time while the concentration of CO₂ increases. At some point in time, the concentrations of H₂CO3 and CO₂ will be equal and [H₂CO₃]/[CO₂] = 1 (state 1). Since I told you what Keq for the hydration of carbon dioxide is, you know that state 1 is not at equilibrium since Keq[H2O] ≠ 1 (i.e., K_eq[H₂O] ≠ [H₂CO₃]/[CO₂] at state 1). The concentrations of H₂CO₃ and CO₂ continue to change with time until the solution reaches the state of chemical equilibrium (state 2), at which point the ratio of products to reactants remains constant and [H₂CO₃]/[CO₂] = K_eq[H₂O].

If you start with 100% CO₂, you will observe that the concentration of CO₂ begins to decrease with time while the concentration of H₂CO₃ starts to build up. Although the concentrations of reactants and products started out much closer to their equilibrium values for this scenario, the system reaches the same equilibrium as in the first scenario.

This thought experiment illustrates a key point: the final state—i.e., the chemical equilibrium—does not depend on the initial state.

The State of the 100% CO2 (aq.) is More Stable Than the State of 100% H2CO3 (aq.)

From the K_eq for the hydration of carbon dioxide, you know that the reaction strongly favors CO₂ and H₂O. Therefore, you know that CO₂ (aq.) is at a lower energy than H₂CO₃ (aq.). We define a quantity called the Gibbs free energy (G), which is the energy in a particular state. This example shows two states: 100% CO₂ (aq.) and 100% H₂CO₃ (aq.). For any reaction, we can define the change in G of a reaction that proceeds from a state with 100% reactant to a state with 100% product as ΔG_rxn = G_(product) – G_(reactant). Because the value of G changes with temperature and concentration, we define a set of conditions under which ΔG_rxns can be compared to one another. Under these conditions, called “the standard state”, concentrations are 1 M, the pressure is 1 atmosphere (atm), and the temperature is constant. The difference in the Gibbs energies of two states under standard state conditions is denoted as ΔG°_rxn. In the case of the hydration of carbon dioxide, there is a ΔG°_rxn associated with the hypothetical reaction in which all the carbon dioxide (1 M, aqueous) is converted to carbonic acid (1 M, aqueous) at 298 K (room temperature). We know from the position of the equilibrium (it favors reactants) that the state of 100% CO₂ (aq.) is more stable (has less G, as depicted in the slide) than the state of 100% carbonic acid (aq.). You might wonder why there is any conversion of CO₂ to carbonic acid if the state of 100% CO₂ is more stable.

All Systems Tend Towards a State of Lower Gibbs Free Energy

The answer is that the free energy of the system at equilibrium, which contains a mixture of the different chemical species, has an even lower G associated with it. This graph depicts the relative free energy levels of the system for different ratios of reactants and products. At equilibrium (where [H₂CO₃]/[CO₂] = K_eq[H₂O]), the amount of G in the system is lower than both the state of 100% CO₂ and the state of 100% H₂CO₃. The take home point is that all systems approach the state that possesses the least Gibbs free energy. This state is the equilibrium state, where the concentrations of products and reactants stop changing. No matter what ratio you start with, the species react to give the same equilibrium ratio of concentrations because that is the lowest energy state.

The Slope of the Red Line

Now that you know that the position of the chemical equilibrium is the state of lowest Gibbs energy, let’s take a closer look at the graph that we constructed to describe the Gibbs free energy diagram for the interconversion of CO₂ and carbonic acid in aqueous solution. The line represents the Gibbs free energies at any state between the two pure states. For each state (or point) along the line, we can define a ΔG as the slope (gradient) of the curve at that state. We shall not be concerned with how we can accurately determine the slope of each point on the curve as that would require more advanced mathematical treatments. Instead we can quite accurately estimate the slopes by redefining ΔG as the change in G of the system as it proceeds from one state to another state via an infinitesimally small step. Therefore, for any two states along the line that vary by very small increments, ΔG = G_final - G_initial.

Based on that we can predict the direction in which the concentrations will change. The concentrations will always change towards the state of lower free energy. For example, the ΔG between A_final and A_iinitial in the plot above is negative; therefore, the step will occur spontaneously towards A_final. The ΔG between C_final and C_iintial is positive; therefore, the step is disfavored in that direction (but is favored in the reverse direction). For each point along the curve (i.e., each set of concentrations of products over reactants) you can do the same type of analysis and figure out whether reaction will occur in the defined direction. Steps occur spontaneously in the direction for which ΔG is negative until equilibrium is reached, at which point ΔG = 0. At equilibrium, a change in the net concentrations in any direction will result in a positive ΔG. You have reached a dynamic state in which molecules are interconverting between species, but there is no net change in concentration because there is no driving force.

There is a Quantitative Relationship between ΔG°rxn and Keq

We started this lecture by asking how one can tell which direction is favored for a chemical reaction. We said that it is necessary to understand the concept of chemical equilibrium in order to answer that question. Over the last few slides, we have intuitively related K_eq to the value of ΔG°_rxn. We said that when K_eq is less than 1 (in the case of the hydration of carbon dioxide), it means that the state of 100% CO₂ is more stable and hence has lower G than the state of 100% H₂CO₃. We now want to understand the relationship between K_eq and ΔGorxn in a more quantitative manner.

On the last slide, we introduced another term called ΔG, the slope (gradient) of the curve at any state (or the change in Gibbs free energy associated with an infinitesimally small step from one state to another). We learned that reactions proceed towards a state of chemical equilibrium in which ΔG = 0. We can employ a very useful equation that relates Keq to ΔG°_rxn. For the representative reaction of A + B <==> C + D, DG = DG°_rxn + RT ln ([C][D]/[A][B]), where T is temperature in degrees Kelvin and R is the ideal gas constant. We know that when the system is at equilibrium, DG = 0 and [C][D]/[A][B] = K_eq; therefore, at equilibrium this equation becomes DG°_rxn = –RTln(K_eq).

ΔG°rxn Tells Us Which Direction Is Favored (Which Atoms Form Which Bonds)

Using the expression derived in the last slide (ΔG°_rxn = –RT ln K_eq), we can now work out conditions involving ΔG°_rxn that will tell us which side of a reversible reaction is favored. If the equilibrium constant for a reaction is greater than 1, then ΔG°_rxn would be negative (< 0). This tells us that the final state with 100% B has less G compared to the initial state with 100% A and the reaction will proceed spontaneously with a release of energy. For a reaction with Keq < 1, ΔG°_rxn is positive (> 0). Therefore, the final state with 100% B now has more G compared to the initial state with 100% A. In order to convert a substantial amount of reactants A to products B, energy is required. The reaction is disfavored relative to the products. Finally, when K_eq = 1, ΔG°_rxn = 0, and the amount of G in the initial and final states are equal. Neither the initial state and the final state is favored, and the reaction proceeds to give equal amounts of products and reactants.

How Does Nature Drive Disfavored Reactions?

The cell is a complex system that must be able to make and break down molecules. Thermodynamics tells us that when a reaction is favorable in one direction, it is unfavorable in another direction. How then does Nature accomplish the feat of getting reactions to go in either directions depending on the requirements of the cell? Obviously, Nature must use energy to drive reactions in the disfavored direction. The most common energy currency in a cell is called adenosine triphosphate (ATP). It is a pretty special molecule and we will take a closer look later in the course. What you need to know now is that Nature has devised ways to carry out disfavored chemical reactions, typically by coupling the energy released in a very favorable reaction (such as ATP hydrolysis as shown, where certain chemical bonds in ATP are broken, and the ΔG°_rxn for the process is large and negative) to the disfavored reaction. In this way, when we consider the coupled processes together, the overall ΔG°_rxn is negative and thus favorable.

Chemical Equilibrium and Thermodynamics

This slide summarizes what we have just gone through about chemical equilibrium and thermodynamics. When we start with a solution with 100% H₂CO₃, the concentrations of H₂CO₃ and CO₂ will change with time until the system reaches equilibrium, where [H₂CO₃]/[CO₂] = Keq[H₂O], the Gibbs free energy (G) is at its minimum and where ΔG = 0. When the system reaches equilibrium, it will stay there for an infinite amount of time until it is perturbed by some external factor. This is exactly what happens in our flask analogy. Given infinite time, every reaction in the flask will eventually reach equilibrium (no matter how slow the process takes).

Before we end our discussion of chemical equilibrium and thermodynamics in the next slide, it is worthwhile to take note that for any reaction, two parameters do not change in the process of approaching equilibrium (under constant temperature). These are K_eq and ΔG°_rxn. These parameters are directly related to the G in the state of 100% reactants relative to the G in the state of 100% products and are only dependent on the identity of the reaction, and temperature.

Cells Are Not At Equilibrium

One final point to appreciate: cells are always changing. They grow, they divide, they respond to environmental stresses in order to survive. You can appreciate that if they are in a constant state of flux, they can’t be at equilibrium. At equilibrium, there is no net change in concentrations. A cell at equilibrium is a cell in which nothing is changing and that is a dead cell. Most chemical processes in a cell are away from equilibrium where ΔG is not equal to zero, and there is thus always a driving force for change (towards equilibrium). In the next lecture, we shall try to understand how the cells prevent themselves from reaching equilibrium.

Table of Contents

a. Le Chatelier’s Principle: A system at equilibrium, subjected to a stress,will adjust to relieve the stress and restore the equilibrium

b. Acidity, K_a and pK_a

c. The Henderson-Hasselbalch equation

d. Application of Le Chatelier’s Principle in cells

How Does a Plant Trap CO2 if the Reaction is not Favorable?

Chemical equilibrium is a very important concept that you will see throughout the course. It can be used to describe any process that is reversible. We have used the example of hydration of carbon dioxide to illustrate how chemical equilibrium can be employed to describe chemical reactions.

Chemical equilibrium can also be used to describe processes that involve state changes, such as the dissolution of carbon dioxide gas into water.

Here is an animation of an unrelated reaction (for illustrative purposes only):

Note that this process is the first step that must occur in order for plants to utilize carbon dioxide during photosynthesis. To be able to use carbon dioxide efficiently, plants must have a way to ‘trap’ high levels of carbon dioxide from the atmosphere.

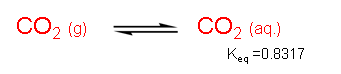
In the equilibrium between gaseous carbon dioxide and aqueous carbon dioxide, K_eq = [CO₂(aq.)]/[CO₂(g)] = 0.8317. Based on our understanding of chemical equilibrium (K_eq < 1), we know for a fact that the equilibrium favors carbon dioxide in the gaseous state, if only by a little. How then do plants ‘trap’ high levels of carbon dioxide? Plants need a stable pool of a CO₂ equivalent to use to make sugars.

We just learned that carbon dioxide can react with water to form carbonic acid. Perhaps this is a way to retain carbon dioxide in water (and hence in plants). However, we also learned that the Keq for this process is 3.09 x 10^-5 M^-1, a value that is far less than 1. Therefore, aqueous carbon dioxide (CO₂(aq.)) is favored over carbonic acid by a significant amount.

If the only equilibria that mattered were the dissolution of carbon dioxide in water and the reaction of carbon dioxide with water to form carbonic acid, we could say that most carbon dioxide remains in the form of CO₂ gas. However, there is another equilibrium we must consider: the ionization of aqueous carbonic acid in water to form bicarbonate.

Le Chatelier's Principle

In the ionization of carbonic acid, a H⁺ ion is transferred to water to form the hydronium ion (H₃O⁺) and the bicarbonate ion (HCO₃^-). This form of ionization is commonly referred to as an acid-base equilibrium because carbonic acid (the acid) is actually in equilibrium with bicarbonate (the base). The Keq (=[H₃O⁺][HCO₃^-]/[H₂CO³][H₂O]) for the acid-base equilibrium is found to be 4.46 x 10^-6 M^-1, which indicates that even this ionization process is not favorable. As you will see, however, even though the Keq favors reactants, almost all of the H₂CO₃ in the cell dissociates to form HCO^3-.

You can appreciate that if most of the H₂CO³ is driven towards HCO₃^-, then more CO₂ (aq.) will react to form H₂CO³, that in turn, will lead to the dissolution of more CO2 gas to form CO₂ (aq.). This is an example of Le Chatelier’s Principle, which we will discuss shortly. The example above shows that by coupling equilibria, you can end up with a significant amount of HCO₃^- which serves as a source for CO₂ for biosynthetic processes.

In order to appreciate the above example more fully, we need to examine the third equilibrium in a more detailed manner. First we need to understand the concept of acidity.

The Concept of Acidity

A molecule is said to be acidic when it is able to give up a proton (H⁺). Acidic molecules usually contain highly polar X-H bonds (where X = electronegative atom), which can be broken easily to form a H⁺ and an X^-. In many acidic molecules, such as H-F, H-Cl or –COOH, there is only one such X-H bond that can be broken (i.e., only one H⁺ can be given up). These are known as monoprotic acids.

In the case of a diprotic acid such as carbonic acid, there are two O-H bonds that are highly polar (due to the high electronegativity of oxygen). This slide depicts one of the O-H bonds in carbonic acid being broken to give H+ and HCO3^-.

Because H⁺ ions are highly unstable on their own, they are bonded to water molecules to form hydronium ions (H₃O⁺). Not shown on this slide is the fact that a second ionization can take place where the bicarbonate loses a H⁺ ion to form the dianionic carbonate (CO₃^2-) ion.

When evaluating a molecule’s acidity, the two relevant states are the protonated and deprotonated forms of the molecule. When an acid gives up a proton (when it is deprotonated), its covalent structure changes slightly because one of its atoms is no longer bonded to a hydrogen atom. The deprotonated molecule, also called the conjugate base form of the molecule, is left with one additional electron that used to be the hydrogen atom’s valence electron; the hydrogen atom, in turn, becomes the hydronium ion. Therefore, a neutral acid upon deprotonation forms a negatively charged conjugate base. Likewise, a positively charged acid becomes a neutral conjugate base upon giving up a proton. At equilibrium, the concentration of protonated and deprotonated molecules is constant (but not necessarily equal).

The Concentration of H2O Doesn't Change Significantly During Ionization

We can write a Keq equation (= [H₃O⁺][HCO₃^-]/[H₂CO₃][H₂O]) for the ionization process of carbonic acid. The concentration of water (in water) is about 55 M and does not change significantly during ionization. Therefore, a new equilibrium constant Ka is often written where K_a = K_eq[H₂O] = [H₃O⁺][HCO₃^-]/[H₂CO³]. K_a is known as the acid dissociation constant and is a measure of whether an acid is a strong or weak acid (as discussed in the next slide). In general, K_a = [H₃O⁺][A^-]/[HA], where HA is the protonated form of the molecule (the acid) while A^- is the deprotonated form of the molecule (the conjugate base). Since carbonic acid is a diprotic acid, there are two K_a values; one for the acid-base equilibrium between carbonic acid and bicarbonate (K_a1), and the other for the equilibrium between bicarbonate and carbonate (K_a2).

The Acidity of a Molecule is Often Expressed in Terms of pKa (-log Ka)

The acidity of a molecule is often expressed in terms of pK_a (-log K_a).

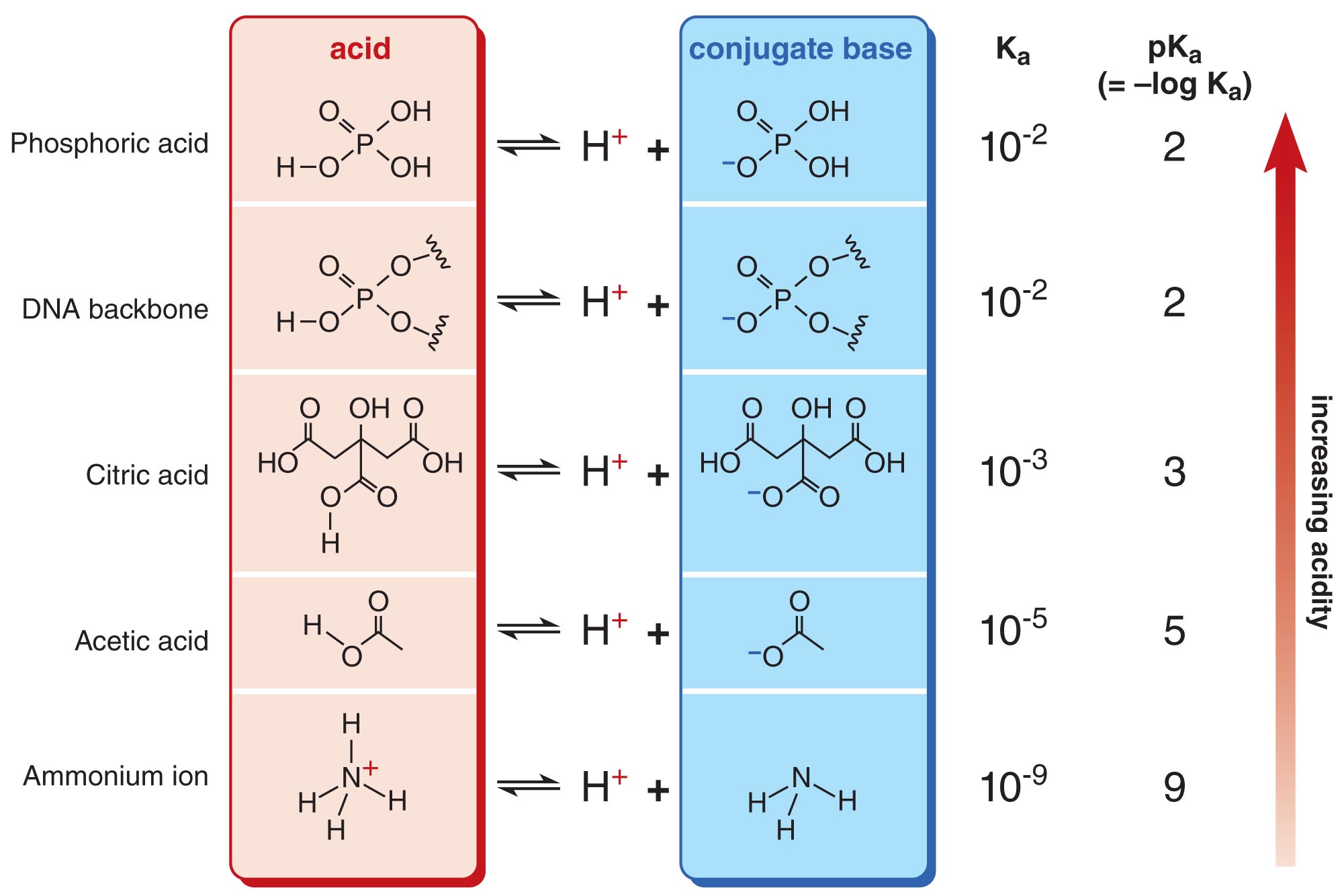
For convenience, the acidity of a molecule is usually indicated by its pK_a value rather than by its K_a value. K_a and pK_a are related by the simple equation pK_a = –log(K_a). Molecules with lower pK_as are more acidic than molecules with higher pKas. By convention, molecules with pK_a values less than 7 are defined as acidic in water, while molecules with pKas greater than 7 are considered basic in water. The pK_a values of several representative molecules are shown here.

Since we know that pK_a = -log(K_a) = -log(K_eq[H₂O]), a pK_a value smaller than -1.75 (which represents K_eq > 1) would mean that the ionization process is favorable and the equilibrium lies towards the conjugate base. Strong acids like HCl (pK_a ~ -8.0) fall into this category and will completely dissociate into H₃O⁺ and A^- when placed in water. As you can see, all pKa values shown in this slide are positive and hence larger than -1.75 (i.e. K_eq << 1). These acids (which are commonly found in the cell) are therefore considered weak acids and only dissociate into H₃O⁺ and A^- to a very small extent. In other words, the ionization process for these acids is not favorable.

The Sum of all the Acids and Bases Dissolved In a Solution is Defined as the pH

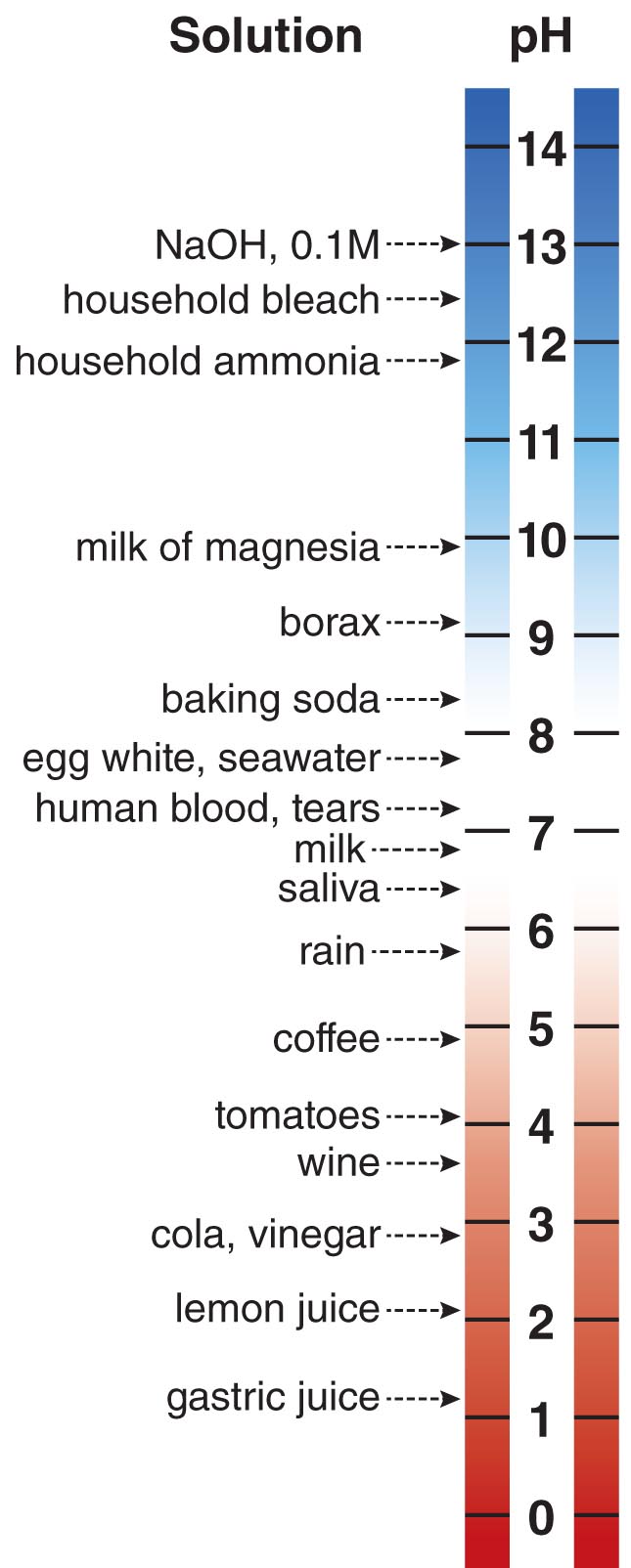
The combination of acidic or basic molecules dissolved in an aqueous solution imparts an acidity or basicity in that solution. The acidity or basicity of a solution is described by a number called its pH. By definition, the pH of a solution is equal to –log [H⁺]. Since in water protons actually become H₃O⁺ cations, pH = –log [H₃O⁺] in water. Therefore, a solution containing a proton concentration of 0.1 M has a pH of 1. As you can deduce, the greater the concentration of protons in solution, the lower the pH of that solution. Neutral aqueous solutions have a pH of 7.0. Acidic solutions such as lemon juice have a pH below 7, while basic solutions such as ammonia-containing window cleaners have a pH above 7.

Click on the simulation below to explore Acid and Bases (www.phet.colorado.edu)

Click to Run

There is a Relationship between pKa and pH: Henderson-Hasselbalch Equation

The protonation state of a molecule depends on both its pK_a as well as the pH of the surrounding solution. The cell contains a large number of species that ionize and the pH in a cell is maintained in most compartments at around 7 (actually, 7.4). The relationship between pKa, pH, and protonation state is given by the Henderson-Hasselbalch equation: pK_a = pH + log ([HA]/[A^–]). This equation can be easily derived from the K_a expression. The Henderson-Hasselbalch equation is very useful for understanding the molecules of life because it allows you to determine what fraction of a molecule exists in a protonated versus deprotonated form at any given pH.

Thus, under physiological conditions (pH ~7), a molecule having a pK_a of 7 exists as an equal mixture of protonated and deprotonated forms. Molecules with pKas less than 7 are mostly deprotonated and exist largely as their conjugate base forms in pH 7 solutions. Conversely, molecules with pK_as above 7 are mostly protonated under physiological conditions. From inspecting this equation, you can deduce the two crucial results that (i) increasing the pH of a solution by one pH unit increases the fraction of deprotonated molecules by exactly 10-fold, and (ii) when pH = pK_a, the concentrations of protonated and deprotonated forms are equal.

The Example of a Cell Helps to Illustrate the Usefulness of the Henderson-Hasselbalch Equation

Let us use the example of the cell to illustrate the usefulness of the Henderson-Hasselbach equation. First of all, the pH inside a cell is maintained at around 7.4. There are numerous acid-base equilibria that exist in the cell, each with a different pK_a. We can use the Henderson-Hasselbalch equation to calculate the ratio of protonated to deprotonated species of each acid in the cell.

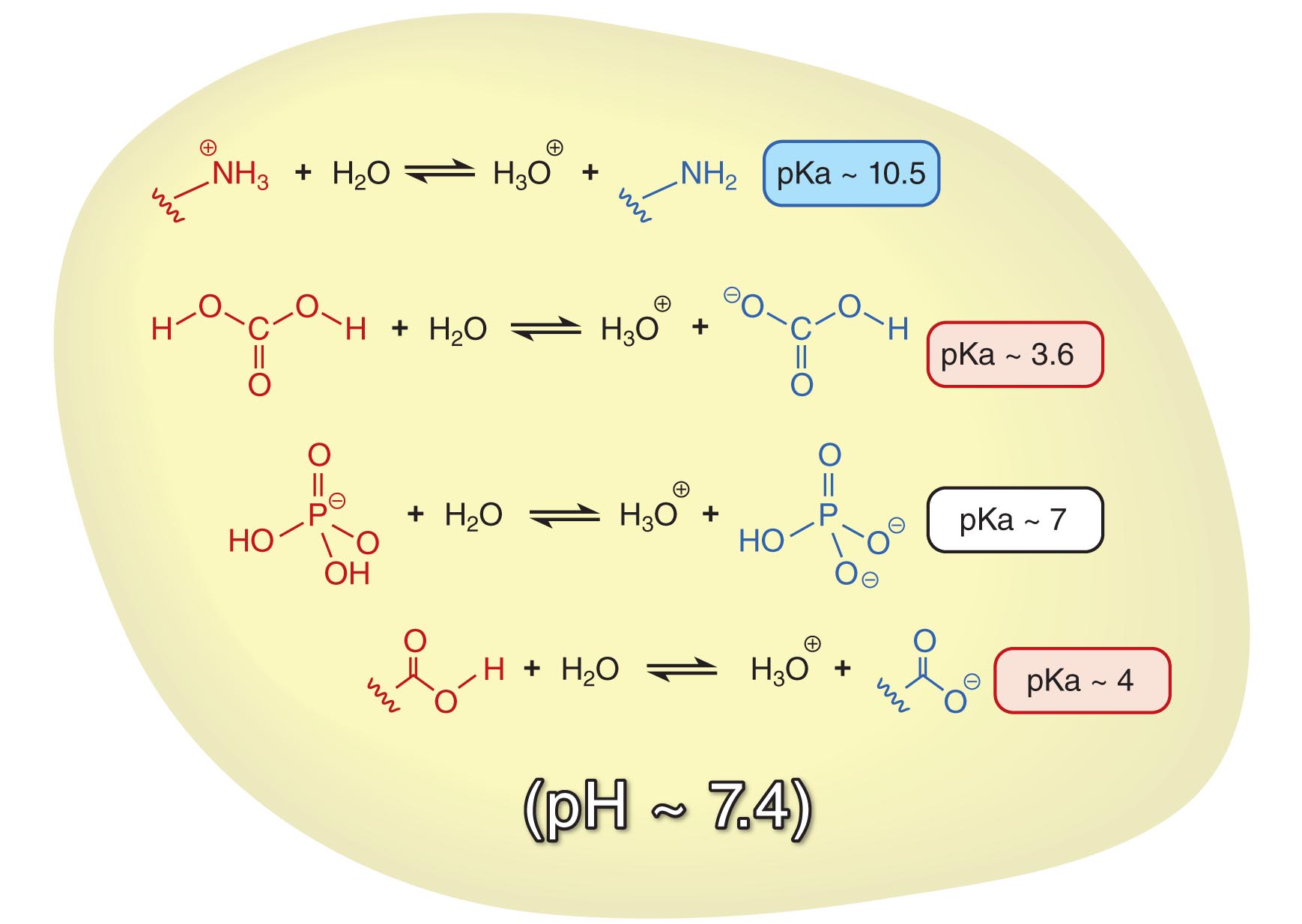
In a solution with a mixture of acids, the overall pH determines the [HA]/[A-] ratios of each acid

The pKa of protonated amines (-NH₃⁺) is around 10.5. At pH ~ 7.4, you will find that the ratio of [-NH₃⁺]:[-NH2] = 103.1:1 ~ 1260:1. This means that at physiological pH (7.4), amines are predominantly protonated. Conversely, based on the pK_a (4.0) of carboxylic acids (-COOH), the ratio of [-COOH]:[-COO-] would be 10-3.4:1 ~ 1:2500. Therefore, carboxylic acids are predominantly deprotonated in the cell. The Henderson-Hasselbalch equation allows us to easily come to a conclusion that there will almost always be a positive charge on amines (due to protonation) and a negative charge on carboxyl groups (due to deprotonation). It also allows us to predict that there are near equal amounts of H₂PO₄^- (acid, pK_a ~ 7.0) and HPO₄^2- (conjugate base) in a solution of pH 7.4.

If you take a look at the acid-base equilibrium between carbonic acid (pK_a ~ 3.6) and bicarbonate, the ratio of [H₂CO₃]:[HCO₃^-] = 10^-3.8:1 ~ 1:6300 at pH 7.4. It therefore seems that the equilibrium now favors the bicarbonate form. Based simply on the value of K_eq for the ionization of carbonic acid combined with the equilibria for dissolution of gaseous carbon dioxide in water and reaction to form carbonic acid, we might have concluded that there is no way to trap carbon dioxide at high concentrations in cells. In fact, because the pH is maintained at 7.4 by other processes, virtually all of the carbonic acid is deprotonated.

Le Chatelier's Principle in Action

The phenomenon that the pH of a solution affects the ratio between two species that are in an acid-base equilibrium, and thus affects other coupled equilibria, is a manifestation of Le Chatelier’s Principle.

Le Chatelier’s principle states that if a chemical system at equilibrium experiences a change in concentration (of any species), temperature, volume or total pressure, the equilibrium will shift in order to counter-act the change.

Increasing the Amount of H3O+ (Much of it from Acide Rain) in the Ocean is Really Bad for Life

Because the carbonic acid-bicarbonate equilibrium favors the bicarbonate side (because of pH), the concentration of H₂CO₃ decreases. The decrease in [H₂CO₃] affects the equilibrium for the reaction between carbon dioxide and water. Based on Le Chatelier’s principle, more carbon dioxide reacts to form H₂CO₃ in order to attempt to increase the levels of H₂CO₃. Similarly, as the levels of aqueous CO₂ decrease due to the formation of carbonic acid (which immediately ionizes to form bicarbonate), Le Chatelier’s principle tells us that more gaseous CO₂ will dissolve into the aqueous environment to make up for that decrease in aqueous CO₂.

Through a set of coupled equilibria and the use of Le Chatelier’s principle, carbon dioxide from the air can thus be easily trapped in the aqueous environment in plant cells in the form of bicarbonate ions. These bicarbonate ions serve as a source of CO₂ which can later be used in the process of photosynthesis. This is a good thing for plants.

It is not a good thing for the ocean in an age where huge amounts of carbon dioxide are generated by industrial processes. As more and more CO₂ dissolves in the ocean, the pH begins to drop because the ocean is not as good as a cell at maintaining a constant pH. Organisms that have calcium carbonate exoskeletons (corals, for example) begin to die because the concentration of carbonate in seawater decreases, and their exoskeletons begin to dissolve (or cannot be renewed due to a lack of carbonate ion to use as a building block). Hence, the three equilibria shown on this slide are coupled to another equilibrium, which is the ionization of bicarbonate to form carbonate.

Le Chatelier’s principle applies to everything that you see in biology and we will come back to this principle in the later lectures.

Key Points