Chapter 2. Applying Models to Mechanical Phenomena

Introduction

This is the second chapter that deals directly with the Energy-Interaction Model. We add all kinds of mechanical interactions to the thermal interactions we treated in Chapter 1. (Note: the term “mechanical” as in the phase “mechanical interactions” is typically used to imply everything other than thermal. Since the Energy-Interaction Model literally applies to every kind of interaction that scientists have ever encountered, we will be just scratching the surface of the realm of applications of this powerful model. We will, however, devote some attention to one area of application that occurs frequently in many phenomena–all kinds of things vibrate, from atoms and molecules to bridges and skyscrapers; that is, they move back and forth or oscillate in very predictable ways.

A fundamental understanding of vibrational (or oscillatory as it is often called) motion is very useful. Therefore, we introduce the Intro Spring-Mass OscillatorModel in this chapter as an application of the Energy-Interaction Model. The IntroSpring-Mass Oscillator Model will also play an important role in Chapter 3 when we develop particle models of matter.

Watch the video below before proceeding.

2.1 Where We Are Headed in this Chapter

In Chapter 2 we continue our focus on interacting systems. We intentionally focus on the systems as they exist before the interaction and then immediately following the interaction; we stay away from the details of what happens during the interaction itself. This is a very general and a very powerful approach. We saw in Chapter 1 that energy transfers are fundamentally related to interactions. When one physical system interacts with another, or when parts of the same physical system interact, we were able to identify energy-systems that either increased or decreased in energy. If the physical system is closed, i.e., we have included all of the energy systems that change during the interaction, then energy conservation tells us that the total of all the increases equals the total of all the decreases. If the physical system is open, then the net change in all of the energy-systems equals the net energy added to the physical system from outside that physical system. We continue this approach in Chapter 2 with non-thermal energy-systems. In discussion/lab activities, you will identify several kinds of energy-systems and the transfers that occur among them. A surprising result for many of us is that when we consider typical activities such as driving a car or riding a bike, most of the energies involved ultimately end up being transferred to various thermal systems. Thermal energy systems seem to have a way of “grabbing and hanging on to” most of the energy. (This tendency has to do with the vast number of particles involved in thermal systems. We explicitly discuss this in Chapter 4.)

Thermal energies are associated with the random or disordered motions of the particles making up matter. In this chapter we turn our attention to energy-systems in which the common motion all of the particles making up the matter is important. We can often describe this common motion with just two variables: a position variable (x) and a speed variable (v). These energies (ones that can be described by position and speed of the entire object) are commonly called mechanical energies.

As you begin the activities of this chapter in your discussion/lab, you might be tempted to ask, “How many kinds of energy can there be?” The answer is simple and reassuring: there are only two fundamental kinds: these are energies that depend on the square of the speed of a particle or object (kinetic energy, abbreviated KE) and energies that depend on the positions or configurations of particles or objects (potential energy, abbreviated PE). All energies, no matter what names we give them, are either a kinetic energy or a potential energy or some combination of the two. This is true for the two energies we have discussed up to this point: bond energy and thermal energy. Bond energy depends on the positions of the atoms making up the molecules, so it is a potential energy. Thermal energy is a combination of the kinetic energies of the individual atoms and the potential energies associated with the motions of the atoms about their equilibrium positions. We will discuss these relations in much greater detail in Chapter 3.

Where are we going with this energy stuff and why? You will begin to see as you carry out the activities and work on the assignments in this chapter that using an Energy-Interaction Model allows us to answer many interesting questions about sports, bikes, objects falling off buildings, and other common (or not so common) everyday activities. Mechanical energies involve position and speed variables, and because transfers of mechanical energy involve work (instead of heat), we need to understand a little more about work. Work involves the notion of forces acting through distances, which means we will have to know a little more about force itself. The payoff is that we will be able to calculate or predict many unknown distances, speeds, and forces without ever having to know the details of the interactions. And the beauty of this approach is that it works for all kinds of physical situations. We don’t have to learn lots of different ways of approaching questions that depend on the particulars of the situation!

Another significant benefit of starting the way we did in Chapter 1 with thermal phenomena is that we can also look much more realistically at real-world phenomena where friction is always present. If you look at a conventional introductory physics text, you will find that for the first third of the book, it seems everyone just pretends that there is no friction! It is as if we lived in a distant galaxy where friction didn’t exist. But that is a pretty idealized galaxy. Because we are treating energy within a general model that works for mechanical energies as well as thermal energies, rather than from a purely mechanics approach, we can deal directly with the transfers of energy to thermal systems and treat a lot of phenomena much more realistically than we could if we narrowly focused on the mechanics of frictionless systems.

2.2 Phenomena, Data Patterns, and Kinds of Questions and Explanations

Data Patterns

Energy never disappears. It just leaves one energy system and reappears in some other energy systems. The total energy stays constant!

Always! Always! Always! Always!

Kinds of Questions and Explanations

• How does energy conservation work with mechanical systems?
• Why do we get hot when we exercise?
• How does an object bouncing on a spring “work?
• What is work?
• What is a force? Is it a push?
• Where does the energy go when this happens?

2.3 Energy-Interaction Model (Summary on foldout #2 at back of this resource packet)

We can apply the Energy-Interaction Model used in Chapter 1 to mechanical energy-systems as well as to thermal and bond energy-systems. Mechanical interactions obey the same rules and can be understood in the same way as the interactions we studied in Chapter 1. Because energy conservation still holds, regardless of the kind of interaction, energy-system diagrams prove to be just as useful in describing the interactions that take place as a ball falls as in describing the interactions taking place in a pot of boiling water. We will also be able to make numerical predictions of various parameters in mechanical interactions, just as we were able to do for thermal interactions.

With thermal and bond systems, we could infer changes in the energy of a system through changes in observable properties, the indicators, such as temperature for the change of thermal energies and change of mass in phase changes. In the mechanical systems introduced below, we infer changes in energy by looking at changes in position and speed. The mechanical energy-systems we describe can exchange energy with each other or with the thermal and bond systems that we discussed in Chapter 1. In Chapter 1, we labeled the energy transferred into a physical system due to a difference in temperature between two objects as heat. In this chapter, we introduce another type of energy transfer to a physical system, which is given the label work, W.

(refer back to Chapter 1 for the Construct Definitions Already Introduced. The only new one here is Work)

Work

Before discussing work explicitly, we will also introduce some ideas about force. These are ideas that we will come back to thoroughly in Part 2 of the course. For right now, we just need a few fairly simple ideas related to force. We can simply think of them as sub-constructs that we will use to make sure we are all on at least a 10th grade level of understanding of work and force and using the same vocabulary. This is all we need for now.

Sub-Constructs Related to Force

Force

Force is the label we give to a fundamental construct that has a prominent place in our models of the dynamics (the details) of change, which we take up in Part 2. This construct is closely identified with our everyday experience with pushes and pulls. Many of the characteristics of pushes and pulls that we are familiar with also apply to forces. Forces have both a magnitude and a direction associated with them. We are all familiar with these ideas. Pushes and pulls have a magnitude (how hard is the push) and in what direction is the push. The technical term used to indicate that a concept has both of these properties is to say it has a vector nature or simply to say it is a vector. We won’t dwell on this in Part 1 of the course.

or in discussion/lab activities for right now. Both parts, direction and magnitude, do, however, affect the amount of energy that one physical system transfers to another physical system. So we need to explore these ideas a little bit further.

One way to represent vector quantities is to simply draw an arrow pointing in the direction the force points (think of the direction of a pull or push) and let the length of the arrow represent the magnitude of the force (how hard the push is pushing). Shown below are several forces represented in this way with arrows.

In these examples force F_A is almost three units in magnitude and points in a direction 45° below the +x axis, or we could say it points southeast. Force F_B is about four units in magnitude and points in the –y direction, or south. Force F_C is about two units in magnitude and points in a direction given by the angle θ with respect to the +x axis.

Force is the agent of interactions of TWO OBJECTS

Forces are the agents of non-thermal interactions between two “objects.” (The quotes around the word “object” signify that it is being used in a general way that includes matter in the form of gases or liquids as well as matter in the solid phase. Sometimes it might even be a single atom or electron. We will omit the quotes from now on, but remember we are using the word object in this more general sense.) Just as there can’t be an interaction involving only one object, there can’t be a force involving only one object.

We normally say, “the force of the (name of an object) on the (name of another object)” to make clear which two objects are involved in the interaction and with the force. For example, we could say, “the force of the bat on the ball” or “the force of the person’s hand on the book.” We write this in symbols as:

F_{bat on ball} and F_{hand on book},

or in symbolic notation,

F _{A on B}

This last notation means object A exerts a force on object B

To realize that this is something you already know and actually does makesense to you think of the following: Use the word “push” in a sentence that refers to you actually pushing. What did you have to say? Did you name an object that you pushed on? Who did the pushing? Can you push without pushing on something? Remember that sometimes it might be something pretty squishy, such as air (which is still a “something,” still an object). Can an object be pushed unless there is “a something” pushing on it? This is what we mean when we say that force is the agent of an interaction. There simply cannot be an interaction without there being two objects. And there can’t be a force without there being two objects.

The Two Forces Involved in an Interaction are Opposite and Equal

Now we come to an idea about forces that makes perfectly good sense if we think about force as the agent of the interaction. But, it is easy to get our head all messed up if we forget this very basic idea and instead think of force as the result of the force instead of simply as the agent of the interaction. Fortunately, we don’t have to worry much about this until we get to the models in Part 2 of the course.

Here is the idea, which does make sense, if we focus on force as described above. The magnitude of F_{A on B} is the same as the magnitude of F_{B on A}. The two forces have the same magnitude, but they point in opposite directions. This important property of forces has been given the label “Newton’s Third Law” and is written symbolically as

F_{A on B} = –F_{B on A}

which simply says that object A pushes as hard on object B as object B pushes on object A, but in the opposite direction. There is one interaction, and the agent of that interaction, the force, has got to be the same in both directions.

Some forces act only when objects are in contact

Let’s consider further the example of the force of the bat on the ball. Does the force of the bat continue to act on the ball after the ball is no longer touching the bat, or does the force act only while the ball and bat are in contact? Recall that force is the agent of interaction, so another way to ask the question is whether the ball and bat continue to interact after they are no longer in contact. The answer is they interact only while in contact. Thus, the force the bat exerts on the ball (and the force that the ball exerts on the bat) acts only while the two objects are in contact. Consequently, we call this force a contact force.

Some forces act even when the objects are not touching. Some act even when extreme distances separate the objects and these are referred to as long-range forces. Think about the force of gravity. The Earth pulls down on all objects near its surface. Note that we have two objects: the Earth and the object being pulled down. We know from everyday experience that the gravitational force of the Earth on an object is present whether the object is touching the Earth or not. Apparently the interaction between the Earth and a nearby object is unlike the force between the bat and the ball. The gravitational force is long range. The interaction and the force, the agent of the interaction, continue to exist even when there is no direct contact.

The force of gravity between our sun and each the planets in our solar system does indeed get weaker as the distance between the sun and the particular planet increases, but it is definitely still there. The gravitational force is truly long range. There are also non-contact forces that act between objects that are not touching, but “die off” or “go to zero” as soon as the objects get more than a little distance apart. Most of the forces that hold atoms together into molecules and hold the particles of solids and liquids together are like this. The interaction and the agent of the interaction, the force, exists, even though the particles are not touching, but the force decreases to zero in magnitude pretty fast as the particles begin to separate just a little bit from each other. We will see examples of this behavior in Chapter 3 when we study the forces between particles. Sometimes this kind of force is said to be short range.

Balanced and Unbalanced Forces

There is one last idea that we will need to use, but is also part of our common experience with pushes and pulls. We can easily imagine two people pushing on a table from opposite sides. If person A pushes harder than person B, the table moves. If the two people push the same, that is, they each exert the same force on the table, but in opposite directions, the table does not move. In the first case, we say the forces exerted by the two objects (the two persons) on the table (a third object) were not balanced, and as a result, the table moved. In the second case, the two objects exerted balanced forces on the table (the third object) and the table did not move. We say the forces exerted by the two persons were balanced.

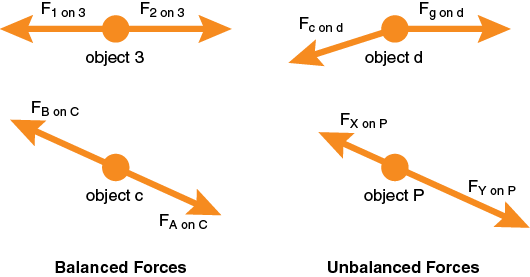
Can you give two reasons why the forces acting on object “3” and on object “C” are balanced and give the two different reasons why the forces acting on objects “P” and “d” are not balanced?

The reason the idea of balanced forces is useful is that sometimes we know the force F1 on 3 for example, but we need to know the force F_{2 on 3} in order to know the work that object 2 does on object 3. If there is reason to believe that the forces from object 1 on 3 and object 2 on 3 are balanced, then we can carry out the analysis and calculate what we want to know. This will become clear in discussion/lab when we start working with forces, springs, pulls, and pushes.

Back to the Construct Work

Now we are ready to make sense of the idea of work as the transfer of energy from one physical system to another physical system or from one object to another object.

Work, W, is a transfer of energy into or out of one physical system by a force exerted by another physical system. The change in energy results from an interaction in which an object moves through a distance parallel to the force exerted on it. In symbols,

where the subscript “parallel” means to multiply only the part of the force and Δx that are parallel to each other. The result is a number without an associated direction. The figure below shows the work done on a box while pushing it a distance Δx.

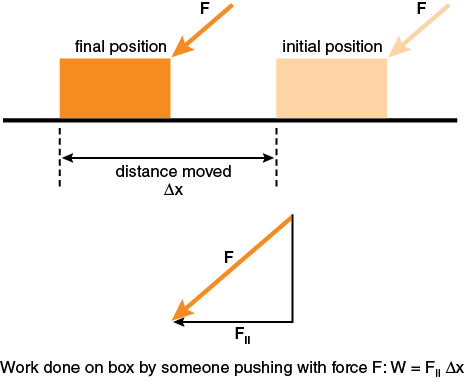
Like heat, Q, work, W, is a scalar (i.e., has no direction associated with it) and is measured in the SI unit of energy, joules. A joule is equivalent to a newton·meter, or J = N·m, since a newton is the SI unit of force. In the example of the box being pushed across the floor at constant speed, energy is transferred from the person to the thermal energy-system of the box and floor. Shown below is an open energysystem diagram for this example.

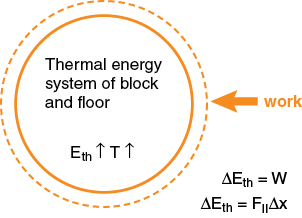
Energy is transferred as work to the physical system of block and floor. If the block moves at constant speed, then the kinetic energy, KE, of the block does not change and the only change in energy systems is the combined thermal energy system of block and floor (something gets warmer due to the friction). Energy was transferred from one physical system, the person doing the pushing, to the block floor physical system during an interaction that involved a force that acted through a distance. Work does not have to result in a transfer to a thermal system, but in this case it did. This example also illustrates that thermal systems can increase (and decrease as well) due to a transfer of energy as work, and not only as heat.

Force of Gravity

An object near the surface of the Earth is attracted to the Earth with a force commonly referred to as the force of gravity. This force is proportional to the object’s mass and fairly constant everywhere on the surface of the Earth. The constant of proportionality is often referred to as “g,” but properly it should have a subscript “E” to indicate that it is the earth that is interacting with the object, and not, e.g., the moon. We will usually include the subscript in this resource packet, and encourage you to do the same. If the downward force of gravity is balanced by an upward force acting on the object, then the object’s motion remains constant (balanced forces). If the object exerting the upward force on the object is a scale or balance, then it reads the “weight” of the object, which is equal in this case of balanced forces, to the gravitational force acting down on the object.

The term weight is often taken to mean the gravitational force. This is OK when forces are balanced and the object’s motion does not change. If the object’s motion is changing, the weight (what a scale reads) can be very different from the gravitational force. (The force of gravity acting on the astronauts in the space shuttle is only slightly less than the force of gravity acting on them when they are standing on Earth, yet they are “weightless” in the orbiting shuttle! We study the interesting state of weightlessness in Part 2 of this course.)

Keeping in mind the reservation mentioned above, we can write:

where m is the mass of the object and gE = 9.8 N/kg near the surface of the Earth. With mass expressed in kilograms and gE in units of N/kg, the weight will be in newtons, N, the SI unit of force. We wrote “g_E” with the subscript “E” to emphasize that the value 9.8 N/kg refers only to the value of g near the surface of the Earth. The value of g on the moon or on Mars will have a different value.

Gravitational Potential Energy

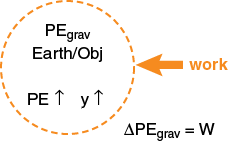
A gravitational potential energy-system exists for each pair of objects interacting by the gravitational force. If we are talking about an object and the Earth, the energy of this system changes as some other object (perhaps you) does work on the object by raising it to a higher elevation. We call this a change in the gravitational potential energy, ΔPE_gravity, of the Earth-object system. This change is simply equal to the work done by the other object and is

where Δy is the change in elevation of the object. Notice that ΔPE_gravity does not depend on distance moved parallel to the surface of the Earth, but only on the change in vertical distance (gravitational force points toward the center of the Earth). The work done on the Earth-object system by something else moving the object further from the center of the Earth, is positive, because the force and change in distance are in the same direction.

Also note that we are imagining that the object is lifted up at a constant speed, so that there is no change in its motion. Thus, all of the work goes into changing the gravitational potential energy of the system. We call this a “potential” energy, because the energy depends only on the relative positions of the object and Earth. It does not depend on the route taken to get to these positions or on the speeds the object and Earth might have.

Note that our expression for the gravitational potential energy gives only changes. Where we put our origin of the coordinate system used to measure “y” does not matter, since we are always subtracting two elevations. If we get sloppy and say an object has a gravitational potential energy of so many joules, we mean it has this amount relative to where we picked the origin of our coordinate system, which is completely arbitrary.

We will come back to this later, but it is worth noting here that there is a connection between the force and the change in the potential energy.

Energy of Motion–Kinetic Energy

Now suppose we do work on an object and move it in a horizontal direction, increasing its speed. Because we have not changed its elevation, we have not changed its gravitational potential energy. But certainly it now has more energy. We know this both from experience and from our definition of work. Where is this energy? It is in the object’s motion. We call this kinetic energy, KE.

If we do work on an object of mass m and change its velocity from vi to vf, then the change in KE is

The next energy system we take up is so important for future work, that we give it its own model: the Intro Spring-Mass Oscillator Model.

2.4 Intro Spring-Mass Oscillator Model (Summary on foldout #3 at back of this resource packet)

Elastic Object

An object, which when deformed (perhaps by squeezing it or stretching it) returns to its original shape.

Spring

A coiled spiral shaped object that is constructed to be elastic over a large range of deformation. Some springs can only be stretched, but if the coils are initially separated, the spring is elastic when both stretched or compressed.

Spring-mass

A spring with an object whose mass is considerably greater than the mass of the spring attached to one end of the spring.

Hanging spring-mass

A spring-mass with one end solidly attached to a support in a manner that the spring hangs vertically with the mass at the bottom of the spring.

Before the mass is attached to the spring, the bottom of the spring (the “free end”) will be at a definite position with respect to the attached end. This is the equilibrium position of the free end without the mass attached. When the mass is attached, the free end of the spring will move to a new, lower position. This is the equilibrium position of the free end of the spring with the massattached.

Force (see discussion earlier in this chapter on Force)

Work (see discussion earlier in this chapter on Force)

Work done on a spring-mass system by an External Agent

The work I do when I pull on the mass increases the PE of the mass/spring system. I can calculate this work: it is simply the product of the force I apply times the distance through which I move while pulling or pushing. The only tricky part is that the force is not constant: F_Iapply = + k y. That is, it is proportional to the distance I have pushed it or pulled it. So I need to take the average force times the distance. The force varies from zero to a max of k y. The average of this is 1/2 ky. When I multiply this average force times the distance, I get the work I do on the system:

Potential Energy of a spring-mass

The expression in the preceding paragraph represents the work I did on the system, so its PE must have changed by that same amount. It doesn’t matter how the spring got stretched (that is, whether it was extended or compressed). If stretched by an amount y, it must have a PE relative to the equilibrium position (with mass attached) of

The change in the spring-mass potential energy, ΔPE _spring-masscan be found using the Energy-Interaction Model in the standard way. Let’s assume in this example that I compress or stretch the spring further from its equilibrium position than when it was in its initial position, yi, to a final position y_f. Therefore, I am doing positive work on the spring-mass system. That is, I am adding energy to the spring-mass system. (The work I do on the spring-mass system will be a positive number of joules.) Thus, its energy must increase. If I don’t change its KE, i.e., don’t change its velocity (the final velocity is equal to its initial velocity), the only energy system that changes is the PE _spring-mass energy system.

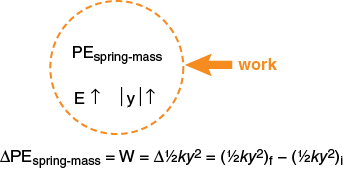
Notice the difference between the equation written just above this sentence and the expression for PE _spring-mass written at the end of the previous paragraph. Can you “tell a story” in your own words what the difference is between these two equations and why they are truly different?

Kinetic energy of a spring-mass

The kinetic energy of the spring-mass system is the same as for any mass that has a speed, v.

where m is the mass of the object hanging on the spring (and part of the spring mass if it is not negligible compared to the mass of the hanging object) and v is the speed (the time derivative of the position, y) of the mass.

The change in the KE _spring-mass is calculated the same way as the change of any energy:

A mass attached to a spring will oscillate if it is pulled away from its equilibrium position and released. Energy is transferred back and forth between the kinetic energy system of the mass and the potential energy system of the spring. If there were no friction, the oscillation would continue forever, with energy transferring back and forth between the kinetic and potential energy systems.

Most physical systems that vibrate back and forth do so like a hanging springmass, particularly when the amplitude of vibration is not too large. Because this motion is so common, it is worth looking at it a little closer.

The maximum value of the PE of this spring-mass system occurs when the mass is at its extreme positions and its speed is zero. Conversely, the KE of the springmass system is a maximum when the mass is at its equilibrium position (y = 0). We know from the last chapter that in the absence of friction, ΔE_tot = ΔKE + ΔPE = 0, or in words, E_tot is a constant. Looking at Etot at any particular time in its cycle of vibration, the energy is still going to be equal to the same total value. Written symbolically, this becomes:

The graph below shows the KE and PE of a spring-mass system as a function of the position from equilibrium. The kinetic energy as a function of y, KE(y), is just the difference between the maximum energy, Emax, and PE(y). This is just another way of expressing conservation of energy for this system. Both PE(y) and KE(y) are parabolas, centered about y = 0. The shape is due to the dependence on the square of y in the expression of the PE.

Although we cannot show it now without investigating the time behavior of the motion of the mass, it turns out that the time-average (that is, the average over time) of the PE and KE are the same, and are consequently both equal to one-half the total energy.

The fact that the time-average potential and kinetic energies are the same has a profound implication for the model of matter that we are about to develop in Chapter 3. This result is true only for a potential energy that depends on the square of the variable. It is precisely the fact that the potential energy is quadratic with respect to position that makes a spring-mass system so special, so universal, and so important.

The lowest point on the PE(y) curve is frequently called the potential energy minimum. Why is the value of the position variable for which the potential energy is a minimum significant? Consider what happens as energy is removed from a system which is oscillating about the equilibrium value of its position (e.g., a real spring-mass system, because of friction, gradually transfers mechanical energy to thermal energy). The amplitude (maximum extent) of the oscillations decreases until eventually, when all mechanical energy has been transferred to thermal systems, the system comes to rest at the equilibrium position, the position of the potential minimum.

Now consider any physical system that oscillates and which will settle down to a stable position as energy is transferred to thermal systems. That stable equilibrium position represents the physical state where potential energy is smallest. (All of the PE and KE have been transferred to thermal systems.) The potential energy must increase as y increases (either positively or negatively) away from zero, the equilibrium position. Now nature seems to prefer smooth changes of things like potential energies. The simplest smooth mathematical function that increases for both positive and negative y is y². When we look at real physical systems, it turns out that sufficiently close to the minimum, the potential energy always “looks parabolic”! This is a result with far reaching consequences. It implies that anyoscillating system behaves just like our simple spring-mass system, at least forsmall amplitudes of oscillation! What’s important is not that the spring-mass system is so special itself; it is, rather, that the behavior of the spring-mass system represents a truly universal behavior of any oscillating system! We will use this property shortly when we model the real atoms of liquids and solids as “oscillating masses and springs.”

2.5 The Connection Between Force and Potential Energy

(This is relationship (8) in the Blue Summary of the intro Spring-Mass Oscillator Model and relationship (2) in the Intro Particle Model of Matter)

There is a relationship between a potential energy and the force that is associated with that potential. This relationship has a useful graphical representation that will help us better understand the spring-mass potential energy and, in Chapter 3, the potential energy associated with the bonding between atoms.

The figure shows the potential energy of a spring-mass system. Marked on the figure are the positions where the force exerted by the spring has the greatest and the least values. If pulled or pushed to some value of the position y, what do we know about the restoring force of the spring?

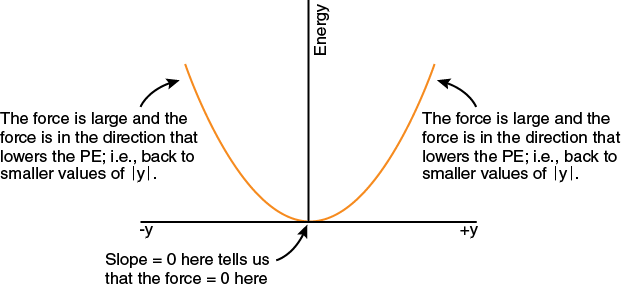
Without derivation, we simply state the result that the force exerted by the spring is equal to the negative of the derivative of the PE with respect to y. Graphically, the force is the negative of the slope of the PE vs. y curve. Rather than worry about the negative sign here, however, we simply focus on the fact that the spring always tries to get back to its equilibrium position. This is what tells us the direction of the force.

For any potential energy, it is true that the magnitude of the force associated with that potential energy is equal to the derivative of the potential energy with respect to the position coordinate associated with the force. Using the symbol r for generality, we can write this symbolically as:

This is a general result that is true for the force associated with any potential energy¹. Since the value of the slope gives the magnitude of the derivative of a function, the steeper the slope of a PE curve plotted against its position variable,the greater the magnitude of the force. The restoring force of the spring (or anything that oscillates) will be zero when the slope is zero, which occurs at the equilibrium point, i.e., where the object comes to rest when it stops vibrating.

2.6 What Energies are Fundamental

It turns out that gravitational potential and spring potential energies we discussed above are examples of one of the two fundamental types of energy–the type that depends on the positions of masses. An energy that depends only on the relative positions of the particles (objects), and not on their past history (the path they took) or on their speeds, is called a potential energy. “Positional energy” is a more descriptive word, but for historical reasons, these are labeled potential energy.

The second fundamental type of energy depends only on the speeds of particles (objects). This kind of energy is called energy of motion or kinetic energy.

All of the various kinds of energy fit into one of the two fundamental types. For example, chemical bonds involve the electric potential energies that depend on the locations of the electrons of the atoms as well as their kinetic energies as they whirl around the nucleus. Thermal energy is a combination of the kinetic and potential energies of individual atoms due to their random motions. Bond energy is a potential energy due to the force individual atoms exert on each other. The elastic energy of a spring is a potential energy because it depends only on the positions of the elements of the spring, not on their speeds. When an object rotates, it has energy due to its rotational motion—rotational kinetic energy.

One energy is as good as any other—almost. On a microscopic scale, energy is energy and any kind can be turned into any other kind. But on a macroscopic scale, where lots of particles (atoms and molecules) are involved, it turns out that all kinds of energy can be turned into thermal energy, but there are restrictions on turning thermal energy back into other kinds. We can convert some, but not all thermal energy to other forms. (We delve into the mysteries of entropy and the second law of thermodynamics in Chapter 4.)

2.7 Examples of Particular Models of Mechanical Phenomena

Example 1

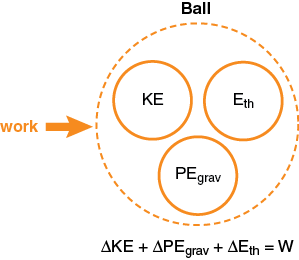
Suppose we consider a baseball thrown by a pitcher. The pitcher’s hand exerts a force on the baseball over some distance parallel to the baseball’s velocity. Thus, the pitcher does a certain amount of work on the ball. Without knowing more details about how the ball was thrown, all we can say is that the work done by the pitcher's arm on the baseball equals the total change in energies of all other energy-systems of the ball. The natural way to model this situation is to treat the baseball as an open physical system.

and W = F|| Δx, where Δx is the distance the pitcher’s hand moved as s/he threw the ball parallel to the direction the ball traveled. This is about all we can say without having more information.

Perhaps we want to estimate the average force the pitcher exerts on the ball during the throw. If the throw is horizontal, there will be no change in gravitational potential energy. If we assume for now that we are focusing on the speed of the ball just after it is thrown, then air resistance will not cause significant energy to be transferred to thermal energy-systems. Thus, we can simplify the energy-system diagram to:

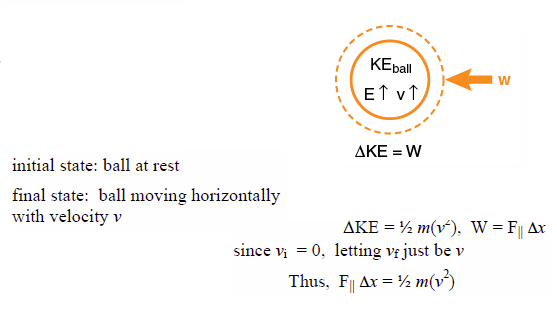
So, if we knew how fast the ball was thrown (which gives us ΔKE), we can determine a value for the force exerted on the ball by the pitcher by making a reasonable estimate for the distance Δx.

Example 2

Instead of being interested in the force the pitcher exerts on the ball when s/he throws it, we might be interested in how much energy the pitcher uses to make a large number of throws. In this case the natural approach is to include the pitcher in the energy-system diagram and not focus on the work done by the pitcher.

We create a closed physical system consisting of the pitcher and the ball.

Note the sign of the change in energy of the pitcher. Does this make sense? You should be able to calculate how many food (big C) calories the pitcher burns after throwing say 100 pitches with the ball averaging 50 miles per hour as it leaves the pitcher’s hand. Is this a good way to stay slim and still eat large hamburgers with fries?

2.8 Looking Back and Ahead

We now have quite a few different forms of energy–translational kinetic as well as rotational, thermal, bond, gravitational potential and spring (or elastic) potential energy. A given physical situation could involve any number of these. Energy can be transferred among physical systems either as heat (when there is a temperature difference between two objects) or as work (when one object exerts a force (on another object) that acts through a distance). There are yet other forms of energy that involve electrical interactions, magnetic interactions, and a more general form of the gravitational energy.

By treating thermal interactions and mechanical interactions on an equal footing, we can approach realistic situations without having to automatically assume friction or air resistance is negligible. By now you should be very comfortable with the energy-interaction model. When we encounter new “kinds” of energy, it won’t be a “big deal.” We simply add them to our repertoire of energy-systems that might change in any particular interaction.

Now we are in a position to delve into particle models of matter. Our goal is to be able to understand, in a general or universal way, as many of the properties of matter as we can. As we do this, we will also make a much more direct connection to thermodynamic concepts you have worked with in chemistry courses.

Even as we extend and perfect our energy-interaction model, we recognize that many questions are beyond its reach. For example, our before-and-after approach can’t tell us, “How long did it take an object to fall?” Questions like this involve the dynamics (the details) of interactions. We will spend more time in Part 2 of the course and accompanying course understanding the dynamics of rigid objects. This is fundamentally the relation of force to motion known as Newton’s 2^nd law. Using Newton’s laws and kinematics to describe the details of interactions, we can answer questions that are unanswerable using the before-and-after approach. But for right now, we stick to an energy approach and avoid, as much as possible, the details of interactions