Chapter 1. Scale and Approximation
Introduction
When a biologist does an experiment or completes a calculation, she often strives for quantitative precision. Commonly, however, it is just as important to be able to approximate – to get a ball park sense of the right answer that will rapidly help her to determine the next step in her research. One way to approximate is to make an order of magnitude comparison. Order of magnitude is commonly discussed in terms of the powers of ten – how many times you must multiply a single digit number by ten to obtain the value in question. 1492, for example, is equal to 1.492 x 1000, or 1.492 x10 x 10 x 10. The order of magnitude of 1492, then, is 3. 1620 also has an order of magnitude of 3, but the order of magnitude of 16,200 is 4:
16,200 = 1.62 x 10 x10 x 10 x10
Exponents and Order of Magnitude
Order of magnitude is most easily evaluated when numbers are presented in what is commonly called scientific notation: a number between one and ten is multiplied by ten by a number of times indicated by a small superscript called the exponent.
1492 = 1.492 x 103
16,200 = 1.62 x 104
Exponents also enable us to approximate the ratio of two numbers. We simply subtract one exponent from the other:
16,200/1492 = (1.62 x 104)/(1.492 x 103)
= 1.62 x 10(4−3)/1.492
= (1.62/1.492) x 101
In many cases, we’ll want to know that the exact value of this ratio is 10.86, but as an approximation, exponents tell us that the larger number is an order of magnitude greater than the smaller.
Exponents allow us to make quick evaluations of the relative importance of different quantities. In an illuminating example, the geobiologist Donald Canfield estimated therates of photosynthesis likely on the early Earth, before the evolution of cyanobacteria and therefore before oxygen gas was present in the oceans and atmosphere. In the absence of cyanobacteria that use water as a source of electrons, rates of photosynthesis would have been limited by the availability of electron donors such as reduced iron, hydrogen sulfide, or hydrogen gas. Based on a model of ocean chemistry on the early Earth, Canfield estimated that reduced iron in solution could support photosynthesis at rates of 1.7 to 5 x 1014 moles of organic carbon per year. For most of us, this number isn’t meaningful in and of itself, but when we compare it to other rates, its importance becomes apparent. Today, Earth’s photosynthesis totals about 4 x 1015 moles of organic carbon per year. So total rates of photosynthesis on the early Earth are estimated to have been an order of magnitude lower than the present day.
Similarly, Canfield estimated that on the early Earth photosynthesis and chemosynthesis based on hydrogen gas would have totaled about 3 x 1013 moles of organic carbon per year, and other ways to generate organic molecules would have yielded even less. From this result, we can conclude that iron-based photosynthesis was the principal means of primary production on the early Earth, generating organic carbon at rates an order of magnitude higher than other forms of photosynthesis or chemosynthesis.
We can use exponents to depict both large and small numbers. When the exponent is positive, it tells us how many times we must multiply the number by 10 to obtain our value; when the exponent is a negative number, we divide by 10 instead:
2.5 x 10-1 = 2.5 ÷ 10 = 0.25
One millimeter is 1/1000 of a meter, or 10-3 m.
10-3 = 1 x 10-3 = 1 ÷ 103 = 1/1000
One micron (or micrometer, about the length of a bacterial cell) = 10-6 m.
In our examples above, the number 10 that is multiplied to provide the exponent is called the base number. Systems of exponents using other base numbers are possible. For example, we could write the number 16 in terms of a base number 2 and an exponent:
16 = 2 x 2 x 2 x 2 = 24,...
Length and Time Scales
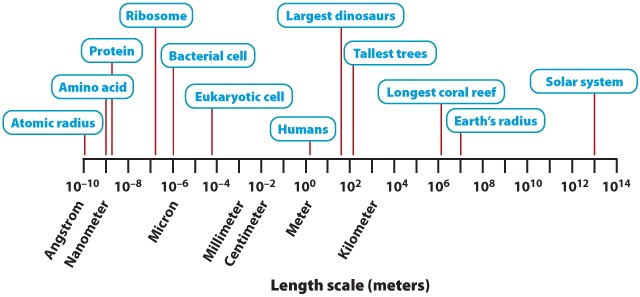
In 1977, Charles and Ray Eames made a short film called Powers of Ten that beautifully captures the meaning of order of magnitude scaling in length (Click Here to Watch). Figure 1 provides a sense of the immense range of length scales relevant to biology. At one end is the ångstrom (10-10 m), used to measure the sizes of atoms, the lengths of chemical bonds, and wavelengths of electromagnetic radiation. A phosphorus atom has a radius of about 1 ångstrom; visible light has wavelengths of 4000 to 7000 ångstroms. An amino acid is about 10 ångstroms, or 1 nanometer (10-9 m), long; folded proteins are commonly a few nanometers across. At the other end of the scale, the Earth has a radius of 107 m, and our solar system is 1013 m across. Developing a sense for order of magnitude size estimates can be helpful in thinking about biological processes.
Time scale is also important in biological thinking, and again, the characteristic time scales of biological processes range from long (evolution) to infinitesimally short (molecular reactions). In thinking about evolutionary biology, it is particularly useful to recognize that generation times are extremely short relative to the time scale of Earth history. In the laboratory, bacteria may reproduce every 20 minutes, and a generation of fruit flies lasts about 10 days. Humans measure generation time in two or three decades (101 years), but our species has existed for nearly 200,000 (2 x 105) years, some 104 human generations. More broadly, life on Earth has existed for nearly 4 billion (109 years) -- 1015 generations of well-fed bacteria!
Logarithms
In 1614, the Scottish mathematician John Napier invented a system of calculating numbers based on exponents that he called logarithms. The logarithm of a number is the number of times a base number must be multiplied by itself to produce the value in question. From the definition, we can see a relationship to orders of magnitude, but whereas order of magnitude uses whole number exponents, logarithms can use fractions. For example,
16 = 101.2
so when the base is 10, the logarithm of 16 is 1.2. Moreover, the base number need not be 10. For example, the base number could be 2:
16 = 24
So in base 2, the logarithm of 16 is 4 (2 x 2 x 2 x 2 = 16). Logarithms are frequently calculated in terms of base 10, but in computer science base 2 is common, and some scientific equations use a value denoted as e (~ 2.7182818) to produce a type of logarithm called the natural logarithm. Logarithms can be obtained from tables and calculators readily available on the Internet.
Logarithms simplify calculations involving large numbers because multiplication is accomplished by adding the logarithms and division is done by subtracting one logarithm from the other. For example, 102 x 103 = 105, and 102 ÷ 103 = 10-1. In a more complicated example, 865 x 124 = 102.937 0 x 102.0934 = 105.0304 = 107,260. You can see why those logarithm tables and calculators come in handy! (In this example, we used only four significant figures in the logarithms, leading, if you calculate it out, to an approximate answer.)
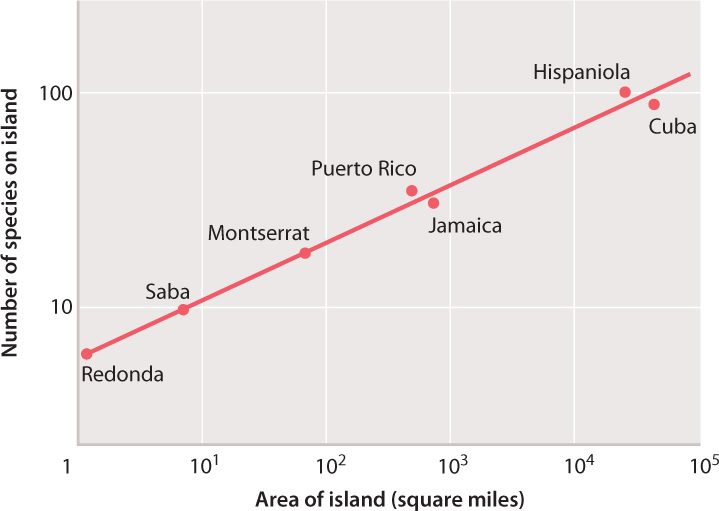
Besides the utility of logarithms in making calculations – perhaps more useful in the seventeenth century than in a world of laptops and iPads – this concept is important because many relationships in nature do not scale linearly, but rather as the logarithm of one or both variables. Take the theory of island biogeography, discussed in Chapter 46. Fig. 46.18 shows the observed relationship between species richness and island size; as predicted by the theory, the number of species on an island scales with the logarithm of island area. (You might try drawing the same graph with island area on the x-axis plotted linearly). Many well-known scales are log-based, including the pH scale used to quantify acidity, the Richter scale for earthquakes, and the decibel scale for loudness.