13.3 Real GDP: A Measure of Aggregate Output
In this chapter’s opening story, we described how China passed Japan as the world’s second-
The moral of this story is that the commonly cited GDP number is an interesting and useful statistic, one that provides a good way to compare the size of different economies, but it’s not a good measure of the economy’s growth over time. GDP can grow because the economy grows, but it can also grow simply because of inflation. Even if an economy’s output doesn’t change, GDP will go up if the prices of the goods and services the economy produces have increased. Likewise, GDP can fall either because the economy is producing less or because prices have fallen.
Aggregate output is the economy’s total quantity of output of final goods and services.
To accurately measure the economy’s growth, we need a measure of aggregate output: the total quantity of final goods and services the economy produces. The measure that is used for this purpose is known as real GDP. By tracking real GDP over time, we avoid the problem of changes in prices distorting the value of changes in production of goods and services over time. So, how is real GDP calculated and what does it mean?
Calculating Real GDP
To understand how real GDP is calculated, imagine an economy in which only two goods, apples and oranges, are produced and in which both goods are sold only to final consumers. The outputs and prices of the two fruits for two consecutive years are shown in Table 13-1. We can see from the data that the value of sales increased from year 1 to year 2. In the first year, the total value of sales was (2,000 billion × $0.25) + (1,000 billion × $0.50) = $1,000 billion; in the second it was (2,200 billion × $0.30) + (1,200 billion × $0.70) = $1,500 billion, which is 50% larger. But it is also clear from the table that this increase in the dollar value of GDP overstates the real growth in the economy. Although the quantities of both apples and oranges increased, the prices of both apples and oranges also rose. So part of the 50% increase in the dollar value of GDP from year 1 to year 2 simply reflects higher prices, not higher production of output.
| Year 1 | Year 2 | |
| Quantity of apples (billions) | 2,000 | 2,200 |
| Price of apple | $0.25 | $0.30 |
| Quantity of oranges (billions) | 1,000 | 1,200 |
| Price of orange | $0.50 | $0.70 |
| GDP (billions of dollars) | $1,000 | $1,500 |
| Real GDP (billions of year 1 dollars) | $1,000 | $1,150 |
366
To estimate the true increase in aggregate output produced, we have to ask the following question: how much would GDP have gone up if prices had not changed? To answer this question, we need to find the value of output in year 2 expressed in year 1 prices. In year 1 the price of apples was $0.25 each and the price of oranges $0.50 each. So year 2 output at year 1 prices is (2,200 billion × $0.25) + (1,200 billion × $0.50) = $1,150 billion. And output in year 1 at year 1 prices was $1,000 billion. So in this example GDP measured in year 1 prices rose 15%—from $1,000 billion to $1,150 billion.
Real GDP is the total value of all final goods and services produced in the economy during a given year, calculated using the prices of a selected base year.
Now we can define real GDP: it is the total value of final goods and services produced in the economy during a year, calculated as if prices had stayed constant at the level of some given base year. A real GDP number always comes with information about what the base year is.
Nominal GDP is the value of all final goods and services produced in the economy during a given year, calculated using the prices current in the year in which the output is produced.
A GDP number that has not been adjusted for changes in prices is calculated using the prices in the year in which the output is produced. Economists call this measure nominal GDP, GDP at current prices. If we had used nominal GDP to measure the true change in output from year 1 to year 2 in our apples and oranges example, we would have overstated the true growth in output: we would have claimed it to be 50%, when in fact it was only 15%. By comparing output in the two years using a common set of prices—
Table 13-2 shows a real-
| Nominal GDP (billions of current dollars) | Real GDP (billions of 2009 dollars) | |
| 2005 | $13,094 | $14,234 |
| 2009 | 14,419 | 14,419 |
| 2013 | 16,768 | 15,710 |
There is an alternative way to calculate real GDP using the data in Table 13-1. Why not measure it using the prices of year 2 rather than year 1 as the base-
Chained dollars is the method of calculating changes in real GDP using the average between the growth rate calculated using an early base year and the growth rate calculated using a late base year.
In reality, the government economists who put together the U.S. national accounts have adopted a method to measure the change in real GDP known as chain-
What Real GDP Doesn’t Measure
367
GDP per capita is GDP divided by the size of the population; it is equivalent to the average GDP per person.
GDP, nominal or real, is a measure of a country’s aggregate output. Other things equal, a country with a larger population will have higher GDP simply because there are more people working. So if we want to compare GDP across countries but want to eliminate the effect of differences in population size, we use the measure GDP per capita—
Real GDP per capita can be a useful measure in some circumstances, such as in a comparison of labor productivity between countries. However, despite the fact that it is a rough measure of the average real output per person, real GDP per capita has well-
Let’s take a moment to be clear about why a country’s real GDP per capita is not a sufficient measure of human welfare in that country and why growth in real GDP per capita is not an appropriate policy goal in itself.
One way to think about this issue is to say that an increase in real GDP means an expansion in the economy’s production possibility frontier. Because the economy has increased its productive capacity, society can achieve more things. But whether society actually makes good use of that increased potential to improve living standards is another matter. To put it in a slightly different way, your income may be higher this year than last year, but whether you use that higher income to improve your quality of life is your choice.
So let’s say it again: real GDP per capita is a measure of an economy’s average aggregate output per person—
ECONOMICSin Action 
Miracle in Venezuela?
 | interactive activity
| interactive activity
The South American nation of Venezuela has a distinction that may surprise you: in recent years, it has had one of the world’s fastest-
So is Venezuela experiencing an economic miracle? No, it’s just suffering from unusually high inflation. Figure 13-2 shows Venezuela’s nominal and real GDP from 2000 to 2014, with real GDP measured in 1997 prices. Real GDP did grow over the period, but at an annual rate of only 2.7%. That’s about twice the U.S. growth rate over the same period, but it is far short of China’s 10% growth.
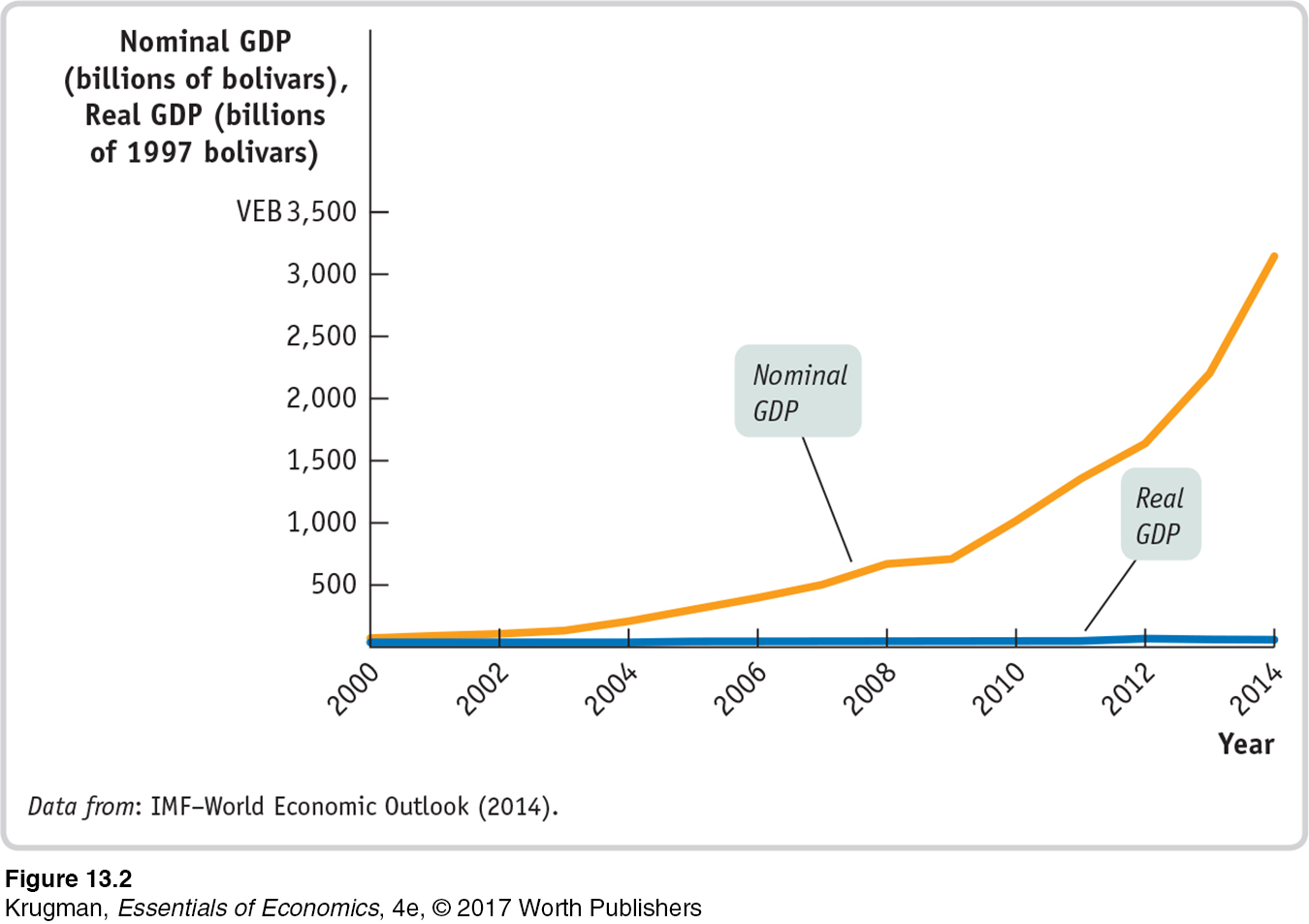
368
Quick Review
To determine the actual growth in aggregate output, we calculate real GDP using prices from some given base year. In contrast, nominal GDP is the value of aggregate output calculated with current prices. U.S. statistics on real GDP are always expressed in chained dollars.
Real GDP per capita is a measure of the average aggregate output per person. But it is not a sufficient measure of human welfare, nor is it an appropriate goal in itself, because it does not reflect important aspects of living standards within an economy.
Check Your Understanding13-
Question 13.3
1. Assume there are only two goods in the economy, french fries and onion rings. In 2013, 1,000,000 servings of french fries were sold at $0.40 each and 800,000 servings of onion rings at $0.60 each. From 2013 to 2014, the price of french fries rose by 25% and the servings sold fell by 10%; the price of onion rings fell by 15% and the servings sold rose by 5%.
Calculate nominal GDP in 2013 and 2014. Calculate real GDP in 2014 using 2013 prices.
In 2013 nominal GDP was (1,000,000 × $0.40) + (800,000 × $0.60) = $400,000 + $480,000 = $880,000. A 25% rise in the price of french fries from 2013 to 2014 means that the 2014 price of french fries was 1.25 × $0.40 = $0.50. A 10% fall in servings means that 1,000,000 × 0.9 = 900,000 servings were sold in 2014. As a result, the total value of sales of french fries in 2014 was 900,000 × $0.50 = $450,000. A 15% fall in the price of onion rings from 2013 to 2014 means that the 2014 price of onion rings was 0.85 × $0.60 = $0.51. A 5% rise in servings sold means that 800,000 × 1.05 = 840,000 servings were sold in 2014. As a result, the total value of sales of onion rings in 2014 was 840,000 × $0.51 = $428,400. Nominal GDP in 2014 was $450,000 + $428,400 = $878,400. To find real GDP in 2014, we must calculate the value of sales in 2014 using 2013 prices: (900,000 french fries × $0.40) + (840,000 onion rings × $0.60) = $360,000 + $504,000 = $864,000.
Why would an assessment of growth using nominal GDP be misguided?
The change in nominal GDP from 2013 to 2014 was (($878,400 − $880,000)/$880,000) × 100 = −0.18%, a decline. But a comparison using real GDP shows a decline of (($864,000 − $880,000)/$880,000) × 100 = −1.8%. That is, a calculation based on real GDP shows a drop 10 times larger (1.8%) than a calculation based on nominal GDP (0.18%). In this case, the calculation based on nominal GDP underestimates the true magnitude of the change.
Question 13.4
2. From 2005 to 2010, the price of electronic equipment fell dramatically and the price of housing rose dramatically. What are the implications of this in deciding whether to use 2005 or 2010 as the base year in calculating 2013 real GDP?
A price index based on 2005 prices will contain a relatively high price of electronics and a relatively low price of housing compared to a price index based on 2010 prices. This means that a 2005 price index used to calculate real GDP in 2013 will magnify the value of electronics production in the economy, but a 2010 price index will magnify the value of housing production in the economy.
Solutions appear at back of book.