1.2 Module 32: Game Theory

WHAT YOU WILL LEARN
 How our understanding of oligopoly can be enhanced by using game theory
How our understanding of oligopoly can be enhanced by using game theory
 The concept of the prisoners’ dilemma
The concept of the prisoners’ dilemma
 How repeated interactions among oligopolists can result in collusion in the absence of any formal agreement
How repeated interactions among oligopolists can result in collusion in the absence of any formal agreement
Games Oligopolists Play
In our duopoly example (from the previous module) and in real life, each oligopolistic firm realizes both that its profit depends on what its competitor does and that its competitor’s profit depends on what it does. That is, the two firms are in a situation of interdependence, whereby each firm’s decision significantly affects the profit of the other firm (or firms, in the case of more than two).
The study of behavior in situations of interdependence is known as game theory.
In effect, the two firms are playing a “game” in which the profit of each player depends not only on its own actions but on those of the other player (or players). In order to understand more fully how oligopolists behave, economists, along with mathematicians, developed the area of study of such games, known as game theory. It has many applications, not just to economics but also to military strategy, politics, and other social sciences.
Let’s see how game theory helps us understand how oligopolies behave.
The Prisoners’ Dilemma
The reward received by a player in a game, such as the profit earned by an oligopolist, is that player’s payoff.
Game theory deals with any situation in which the reward to any one player—
A payoff matrix shows how the payoff to each of the participants in a two-
When there are only two players, as in a lysine duopoly, the interdependence between the players can be represented with a payoff matrix like that shown in Figure 32-1. Each row corresponds to an action by one player (in this case, ADM); each column corresponds to an action by the other (in this case, Ajinomoto). For simplicity, let’s assume that each of our firms can pick only one of two alternatives: produce 30 million pounds of lysine or produce 40 million pounds.
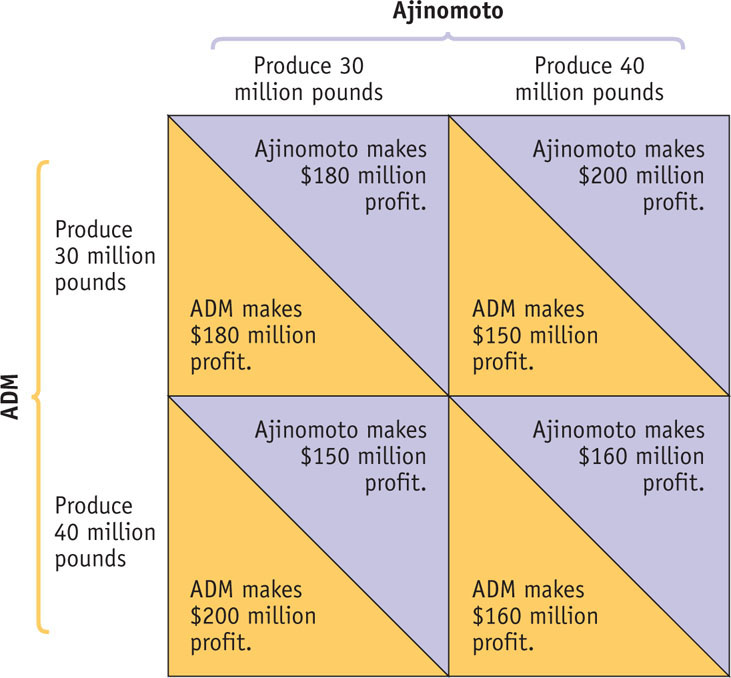
The matrix contains four boxes, each divided by a diagonal line. Each box shows the payoff to the two firms that results from a pair of choices; the number below the diagonal shows ADM’s profits, the number above the diagonal shows Ajinomoto’s profits.
These payoffs show what we concluded from our earlier analysis: the combined profit of the two firms is maximized if they each produce 30 million pounds. Either firm can, however, increase its own profits by producing 40 million pounds if the other produces only 30 million pounds. But if both produce the larger quantity, both will have lower profits than if they had both held their output down.
The prisoners’ dilemma is a game based on two premises: (1) Each player has an incentive to choose an action that benefits itself at the other player’s expense; and (2) When both players act in this way, both are worse off than if they had acted cooperatively.
The particular situation shown here is a version of a famous—
- Each player has an incentive, regardless of what the other player does, to cheat—
to take an action that benefits it at the other’s expense. - When both players cheat, both are worse off than they would have been if neither had cheated.
The original illustration of the prisoners’ dilemma occurred in a fictional story about two accomplices in crime—
So the police put the miscreants in separate cells and say the following to each: “Here’s the deal: if neither of you confesses, you know that we’ll send you to jail for 5 years. If you confess and implicate your partner, and she doesn’t do the same, we reduce your sentence from 5 years to 2. But if your partner confesses and you don’t, you’ll get the maximum 20 years. And if both of you confess, we’ll give you both 15 years.”
Figure 32-2 shows the payoffs that face the prisoners, depending on the decision of each to remain silent or to confess. (Usually the payoff matrix reflects the players’ payoffs, and higher payoffs are better than lower payoffs. This case is an exception: a higher number of years in prison is bad, not good!) Let’s assume that the prisoners have no way to communicate and that they have not sworn an oath not to harm each other or anything of that sort. So each acts in her own self-
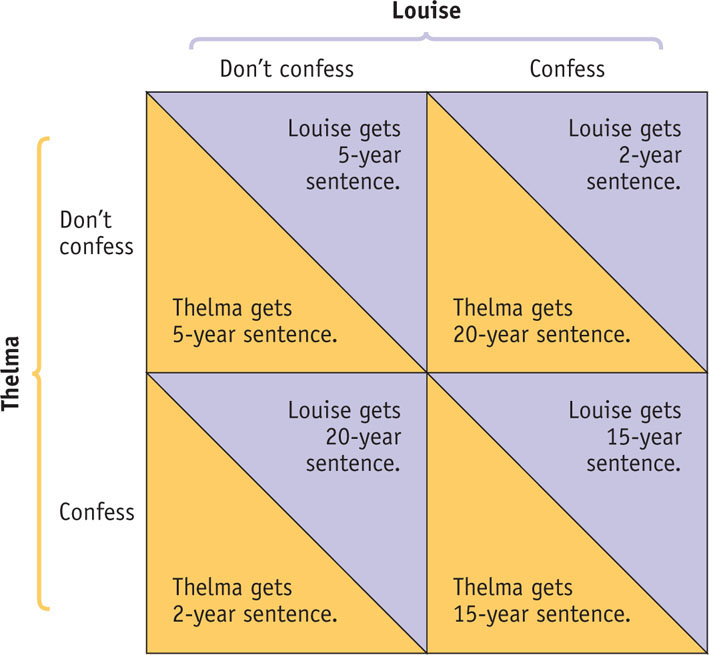
An action is a dominant strategy when it is a player’s best action regardless of the action taken by the other player.
The answer is clear: both will confess. Look at it first from Thelma’s point of view: she is better off confessing, regardless of what Louise does. If Louise doesn’t confess, Thelma’s confession reduces her own sentence from 5 years to 2. If Louise does confess, Thelma’s confession reduces her sentence from 20 to 15 years. Either way, it’s clearly in Thelma’s interest to confess. And because she faces the same incentives, it’s clearly in Louise’s interest to confess, too. To confess in this situation is a type of action that economists call a dominant strategy. An action is a dominant strategy when it is the player’s best action regardless of the action taken by the other player.
It’s important to note that not all games have a dominant strategy—
So if each prisoner acts rationally in her own interest, both will confess. Yet if neither of them had confessed, both would have received a much lighter sentence! In a prisoners’ dilemma, each player has a clear incentive to act in a way that hurts the other player—
A Nash equilibrium, also known as a noncooperative equilibrium, is the result when each player in a game chooses the action that maximizes his or her payoff, given the actions of other players.
When Thelma and Louise both confess, they reach an equilibrium of the game. We have used the concept of equilibrium many times in this book; it is an outcome in which no individual or firm has any incentive to change his or her action. In game theory, this kind of equilibrium, in which each player takes the action that is best for her, given the actions taken by other players, is known as a Nash equilibrium, after the mathematician and Nobel Laureate John Nash. Because the players in a Nash equilibrium do not take into account the effect of their actions on others, this is also known as a noncooperative equilibrium.
In the prisoners’ dilemma, the Nash equilibrium happens to be an equilibrium of two dominant strategies—
Now look back at Figure 32-1: ADM and Ajinomoto face a prisoners’ dilemma just like Thelma and Louise did after the crimes. Each firm is better off producing the higher output, regardless of what the other firm does. Yet if both produce 40 million pounds, both are worse off than if they had followed their agreement and produced only 30 million pounds. In both cases, then, the pursuit of individual self-
Prisoners’ dilemmas appear in many situations. The following Economics in Action describes an example from the days of the Cold War. Clearly, the players in any prisoners’ dilemma would be better off if they had some way of enforcing cooperative behavior: if Thelma and Louise had both sworn to a code of silence, or if ADM and Ajinomoto had signed an enforceable agreement not to produce more than 30 million pounds of lysine.
But we know that in the United States an agreement setting the output levels of two oligopolists isn’t just unenforceable, it’s illegal. So it seems that a noncooperative equilibrium is the only possible outcome. Or is it?
!world_eia!PRISONERS OF THE ARMS RACE
Between World War II and the late 1980s, the United States and the Soviet Union were locked in a seemingly endless struggle that never broke out into open war. During this Cold War, both countries spent huge sums on arms, sums that were a significant drain on the U.S. economy and eventually proved a crippling burden for the Soviet Union, whose underlying economic base was much weaker. Yet neither country was ever able to achieve a decisive military advantage.
As many people pointed out, both nations would have been better off if they had both spent less on arms. Yet the arms race continued for 40 years.

Why? As political scientists were quick to notice, one way to explain the arms race was to suppose that the two countries were locked in a classic prisoners’ dilemma. Each government would have liked to achieve decisive military superiority, and each feared military inferiority. But both would have preferred a stalemate with low military spending to one with high spending. However, each government rationally chose to engage in high spending. If its rival did not spend heavily, this would lead to military superiority; not spending heavily would lead to inferiority if the other government continued its arms buildup. So the countries were trapped.
The answer to this trap could have been an agreement not to spend as much; indeed, the two sides tried repeatedly to negotiate limits on some kinds of weapons. But these agreements weren’t very effective. In the end the issue was resolved as heavy military spending hastened the collapse of the Soviet Union in 1991.
Unfortunately, the logic of an arms race has not disappeared. A nuclear arms race has developed between Pakistan and India, neighboring countries with a history of mutual antagonism. In 1998 the two countries confirmed the unrelenting logic of the prisoners’ dilemma: both publicly tested their nuclear weapons in a tit-
Overcoming the Prisoners’ Dilemma: Repeated Interaction and Tacit Collusion
A firm engages in strategic behavior when it attempts to influence the future behavior of other firms.
Thelma and Louise are playing what is known as a one-
Suppose that ADM and Ajinomoto expect to be in the lysine business for many years and therefore expect to play the game of cheat versus collude shown in Figure 32-1 many times. Would they really betray each other time and again?
A strategy of tit for tat involves playing cooperatively at first, then doing whatever the other player did in the previous period.
Probably not. Suppose that ADM considers two strategies. In one strategy it always cheats, producing 40 million pounds of lysine each year, regardless of what Ajinomoto does. In the other strategy, it starts with good behavior, producing only 30 million pounds in the first year, and watches to see what its rival does. If Ajinomoto also keeps its production down, ADM will stay cooperative, producing 30 million pounds again for the next year. But if Ajinomoto produces 40 million pounds, ADM will take the gloves off and also produce 40 million pounds next year. This latter strategy—
Tit for tat is a form of strategic behavior because it is intended to influence the future actions of other players. The tit-
The payoff to ADM of each of these strategies would depend on which strategy Ajinomoto chooses. Consider the four possibilities, shown in Figure 32-3:
- If ADM plays tit for tat and so does Ajinomoto, both firms will make a profit of $180 million each year.
- If ADM plays always cheat but Ajinomoto plays tit for tat, ADM makes a profit of $200 million the first year but only $160 million per year thereafter.
- If ADM plays tit for tat but Ajinomoto plays always cheat, ADM makes a profit of only $150 million in the first year but $160 million per year thereafter.
- If ADM plays always cheat and Ajinomoto does the same, both firms will make a profit of $160 million each year.

Which strategy is better? In the first year, ADM does better playing always cheat, whatever its rival’s strategy: it assures itself that it will get either $200 million or $160 million. (Which of the two payoffs it actually receives depends on whether Ajinomoto plays tit for tat or always cheat.) This is better than what it would get in the first year if it played tit for tat: either $180 million or $150 million. But by the second year, a strategy of always cheat gains ADM only $160 million per year for the second and all subsequent years, regardless of Ajinomoto’s actions.
Over time, the total amount gained by ADM by playing always cheat is less than the amount gained by playing tit for tat: for the second and all subsequent years, it would never get any less than $160 million and would get as much as $180 million if Ajinomoto played tit for tat as well. Which strategy, always cheat or tit for tat, is more profitable depends on two things: how many years ADM expects to play the game and what strategy Ajinomoto follows.
If ADM expects the lysine business to end in the near future, it is in effect playing a one-

But if ADM expects to be in the business for a long time and thinks Ajinomoto is likely to play tit for tat, it will make more profits over the long run by playing tit for tat, too. It could have made some extra short-
When firms limit production and raise prices in a way that raises each other’s profits, even though they have not made any formal agreement, they are engaged in tacit collusion.
The lesson of this story is that when oligopolists expect to compete with each other over an extended period of time, each individual firm will often conclude that it is in its own best interest to be helpful to the other firms in the industry. So it will restrict its output in a way that raises the profit of the other firms, expecting them to return the favor. Despite the fact that firms have no way of making an enforceable agreement to limit output and raise prices (and are in legal jeopardy if they even discuss prices), they manage to act “as if” they had such an agreement. When this type of unspoken agreement comes about, we say that the firms are engaging in tacit collusion.
Module 32 Review
Solutions appear at the back of the book.
Check Your Understanding
1. Suppose world leaders Nikita and Margaret are engaged in an arms race and face the decision of whether to build a missile. Answer the following questions using the information in the payoff matrix below, which shows how each set of actions will affect the utility, a measure of personal satisfaction, of the players (the numbers represent utils gained or lost).
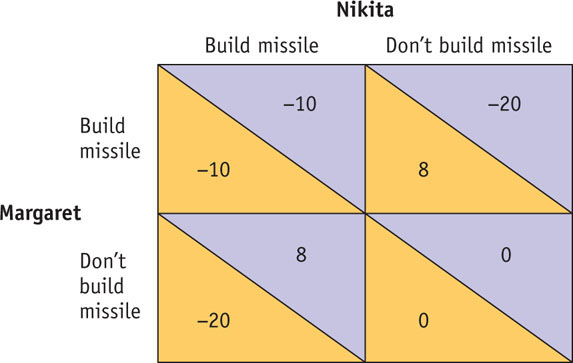
-
a. Identify any Nash equilibria that exist in this game, and explain why they exist.
-
b. Which set of actions maximizes the total payoff for Nikita and Margaret?
-
c. Why is it unlikely that they will choose the payoff-
maximizing set of actions without some communication?
2. Which of the following factors make it more likely that oligopolists will play noncooperatively? Which make it more likely that they will engage in tacit collusion? Explain.
-
a. Each oligopolist expects several new firms to enter the market in the future.
-
b. It is very difficult for a firm to detect whether another firm has raised output.
-
c. The firms have coexisted while maintaining high prices for a long time.
Multiple-
Question
UtJV7RNBqiEHfjvhMSik91ozqW7jBaudgY7CuqxxdFq7OKVFIbxxd/DX5UKrgL6KIWwNRqXmnowEAKpCqXaTA2VXG+LKmFLZKg5qv3Kerh+Ukea5pUqiSZSZqyv7toKfBLmTNnBCDXfhtZr2nYIo4G5m0TgT7Gf41pjR6cpLzkCUNboh6IpBKnvNuLhLSmUfnKM7iMw7fGcrG1+QsSmKDxqRxxFL09p0VLieBb7qxaAzF8eYfoRnuDxn347mq7n6TUjj5htMCD60v/+JLYT4+piy+n436QluQ10bMnS+anrI3d+iFU0pJ3IhsnTKhz8ywzrCHAXgEs9dSLXsnghEgqNLraYL1qX8KTvob8JQM9CF9e4YRoSAaqqQKxFzy2L/3OGES+rL597+rDPl5MnXDvae9Kra7Einw37q1i7sIBo=Question
fubChWIN4mCUvvcI7awF3D67YAB+t721QoK5OpuWR0yfNRHkviNgeQi0rxLi7uJhTJvOaaZfTsQvi32rdQGvK81O7NEOdQQn9XPkZlx+BRRmru27dJUfz1fXMCEuZFFYwADkX0qJM1X0WP4jT5fc7IrhM29P8EK1cWcyf1NAHQfqYXXfNlY3BbLukTWsGfLenK72p1Klq0mrH3HajZiN9lrBIBVVVVfOkirmFxvmy3cT2rzD2RylWDcfNKnD9OmGF2ClQJTDpstIOyovs97G1uqNm5bJsqeruH9eJ0K6KI1Fz0ikUfM/BK5orIdUd3lviBhMoxKMC355wkwtvfZhXUrjtry9jnMN0bIpqCWmpnAnekOe2NrNj/Tf82MrXsHLAp9yZHgjgBxjESX4DHFHkrKDyDZRDjx2WGDAP8i1ZvxO9hEO4WKqUqYG6jc=Question
leiwpkafrgsNWjVPNSxwYC7jRuY3zHXdu+BaK2VddqqVj1kP8pd9RYjAR+pejb1aEJZi4FotOIj3b8XpTnFZgbtEu7afUFFq8Q+YtMiqwwiBylHznBNk30sd015mKpnin1lL+OsC4bFIndq1qZgrDRCkN/YgdkAHKWuK+vlCzR4iq2g2guM9NxlAsQXyL3SU0N0GvQ+8j3+9YvLUzaUIAxFlbh3e+li70xeo6YL2U7WqxdaktyfPHAEpwELWqgLy6p9+AAt/z3E/LT3JaOcIEIgOkYa0eJJqZ9WmY55HSqdTsdB8g85TnNpWfHuwhyt8YNhUKq38HzXd9bOZ7AEdLnFNr4UZYMK0fEswQTuNZHfGuLU3SbqTTigXwrJ3WeboH+3Q/PsZahnjS+G4i9ZzzI92BdKi7wOJfh+CCTcblZs53HucdOtEAiYnFm4pAtHehwY/SaNta7DLfgH+CaFFdp53x/9J4ruY84YgqIQdBbQvbE5MvoZFIeZ9SJnzfgUP4IQqPl9E9q+hqu1eiPnhA4rjM/wHQVfq3oZZU2mxZ8emIaj4Question
qW2HKS60k7RJvYPVUThvy929ZFtxx7cyXXDk9/daDwt632vZiCwz63tsPx1XODkjL7gaZC5pHeNRbtFwEtO6Xj/eb8DE6b8jWKXybzu5ZAnE5KprQIPNnxHeYRyooMorzMSaFY2meMsUqPsgT9p07fMNcv8kUqOr8mzsiDS+poF9yq1raYJXt9A8la+VMSMFsky8YY5/H3cnCUaV5+6e6nIXBtUkBj7pe1j+kovvbs12bWRi4+t4dUA3E135tk9DmClZTygEhAc+eGZf+shfJRu11r2PYnHbpCxKA7P3wa630PuukYCdKA8Y/j9lXAssnC7qE/0eKQ1ruCoOxLbiJ3iGpEedLFWP5677ffE3T+0hHltygdMfmqvmMgu7EUnX5E85rDVtj/jZsIAQdXajtNDNwyTcr6H70pu2cOOmhNPeiuFrdbL6olE/kyaCQi+YnSkVZshy/4A2ku/rtbuWZI0F3qhvEGDsh6ie9I0DlIofq6He3LSXxy4E5nQ/Ai0zwEIIUqh6q7OQ4hlCc7blpeSqVB28FJQYYLOAf67ZThf7VmDigSQbRSeZkEdCTInuLKihf6Dn8HzNYrRP69VSg7114uNmXgpXF8g3DAXk44L80cXzEcDFYSVfP2UWqXuuVcpufIvFvg8z2hr1SmgLynN/lc4HS6eDDu4rRolS6r+lxalsXJhzbmam7S2eH/HB9mHGVg==
Question
2/lxxXbpepjezdAY4o2J4yf6TaRx4HsSZQFrf5/FWsFbsvmiPTzdIUCGFilNRU0KFJc4vSFPe1yYUDDH6EzyOvBpbLnV4kUryWyGbGGGHJSPkWEW7KcvH7u2UbMTfM8aEJ0oHB3ZkLKNQBu0b6HYZA0/yI0OPW+1KlsL2k2ZUEjrMzVZtRT9oZ0ndiAhwj14GMmWw2QKIqby1lMhvuvu034cgUJvXTkZQ1N+A3x9xQMIu3q1DpLODO08YXNbyJMuc6nndJWtPDfao9gfHDsDDoiyRY6T/QCtyy3GG8UxR/qL7ZwlRvyUr/CFucAbHEDuoQogrcuWN/TP1w6dMo+ovPJkVot2d7iO6YJBb+YUUY4YEb0Yen7bXbHKl1iSrtjeFv1Om6S+EMFon+vINfPSLEKVNqd96gbrljA4yb0CVqded73uvoXvblSZQtzOh1e+qCQAR+g9eu8SykdC91rBvj72G91nlG2gwwygBTo1LmPoNbp3PPyIFblW4nOVopNDQEl5AslprHaQHbRrM6zrToZ/PeEllSVr0KCUM0zRPRZQbNaCHzBy2bq+sSAq2g11FHjLqg==Critical-
Draw a clearly labeled payoff matrix illustrating the following situation. There are two firms, “Firm A” and “Firm B.” Each firm must decide whether to charge a high price or a low price. If one firm charges a high price and the other a low price, the firm charging the high price will earn low profits while the firm charging the low price will earn high profits. If both firms charge a high price, both earn high profits and if both firms charge low prices, both earn low profits.
PITFALLS: PLAYING FAIR IN THE PRISONERS’ DILEMMA
PLAYING FAIR IN THE PRISONERS’ DILEMMA
 Let’s reconsider the situation faced by our accomplices in crime, Thelma and Louise. Is it rational for them to confess in the prisoners’ dilemma? They are both criminals, after all, and it’s not unreasonable to think that they would keep their mouths shut out of fear that the other would take revenge for a confession.
Let’s reconsider the situation faced by our accomplices in crime, Thelma and Louise. Is it rational for them to confess in the prisoners’ dilemma? They are both criminals, after all, and it’s not unreasonable to think that they would keep their mouths shut out of fear that the other would take revenge for a confession.
 Yes, it is rational for both of them to confess. To understand the dilemma, you have to play fair and imagine prisoners who care only about the length of their sentences. You cannot change the payoffs in the payoff matrix! Doing so is a little bit like cheating. Luckily, when it comes to oligopoly, it’s a lot easier to believe that the firms care only about their profits. There is no indication that anyone at ADM felt either fear of or affection for Ajinomoto, or vice versa; it was strictly about business.
Yes, it is rational for both of them to confess. To understand the dilemma, you have to play fair and imagine prisoners who care only about the length of their sentences. You cannot change the payoffs in the payoff matrix! Doing so is a little bit like cheating. Luckily, when it comes to oligopoly, it’s a lot easier to believe that the firms care only about their profits. There is no indication that anyone at ADM felt either fear of or affection for Ajinomoto, or vice versa; it was strictly about business.
To learn more, see pp. 335–
