life11e_ch01

Statistical methods are essential scientific tools

Whether we do comparative or controlled experiments, we have to decide whether there is a real difference between the samples, individuals, groups, or populations in the study. How do we decide whether a measured difference is enough to support or falsify a hypothesis? In other words, how do we decide in an unbiased, objective way that the measured difference is significant?

Significance is measured with statistical methods. Random variation is almost always present in any set of measurements. Statistical tests calculate the probability that the differences observed in an experiment could be due to random variation. The results of statistical tests are therefore probabilities. A statistical test starts with a null hypothesis—the premise that observed differences are the result of random variation that arises from drawing two finite samples from the same population. When quantified observations, or data, are collected, statistical methods are applied to those data to see if there is sufficient evidence to reject the null hypothesis.

investigating life

Corals in Hot Water

experiment

Original Paper: Palumbi, S. R., D. J. Barshis, N. Traylor-Knowles and R. A. Bay. 2014. Mechanisms of reef coral resistance to future climate change. Science 344: 895–898.

Rachael Bay and her colleagues did a controlled experiment by bringing corals from the warm and the cool tidal pools into the laboratory and then subjecting them to cycles of heat stress that simulated the conditions that sometimes occurred in the warm tidal pools. The outcome measure was bleaching—the loss of photosynthetic symbionts (dinoflagellates) from the coral bodies.

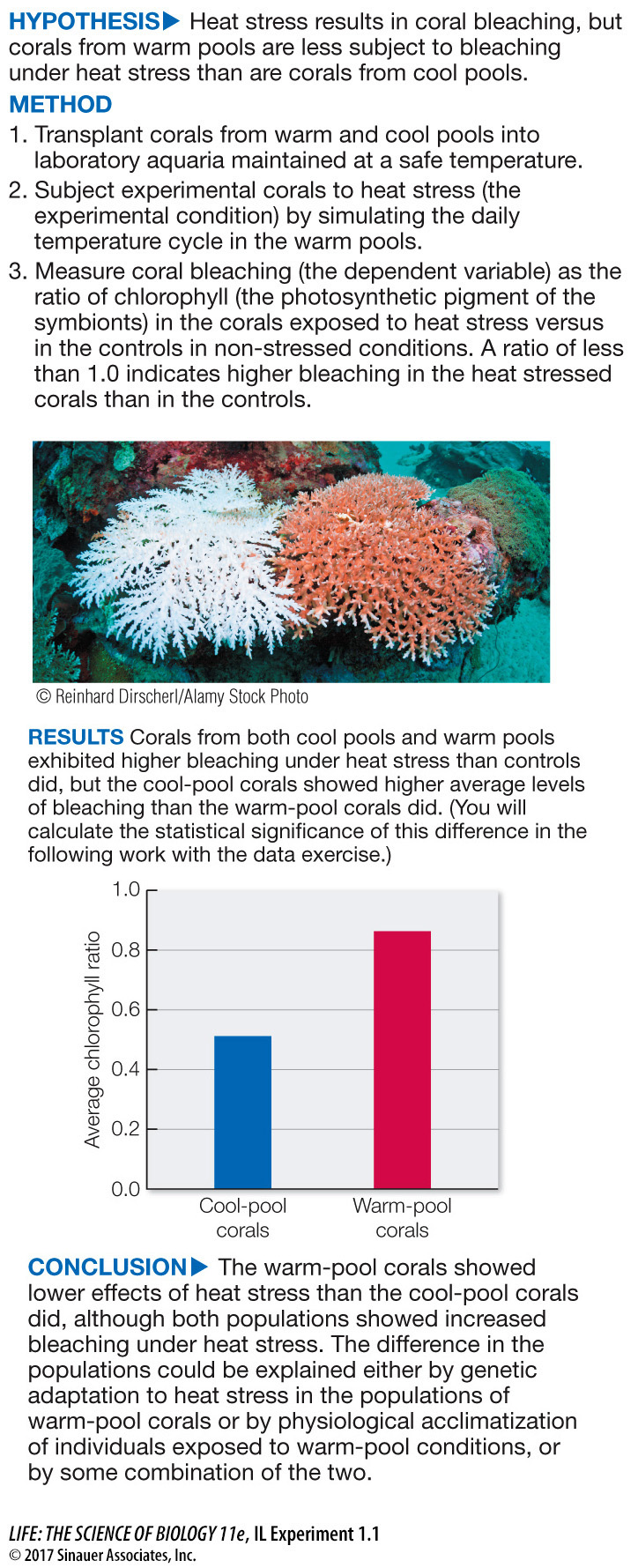
work with the data

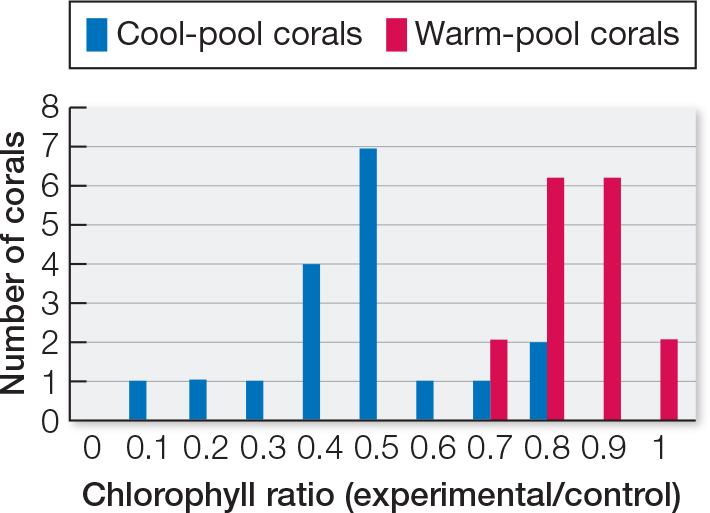
The bar graph in the Results section of the experiment shows that both cool-pool corals and warm-pool corals showed increased levels of bleaching under heat stress, relative to controls. It also shows that the cool-pool corals showed greater relative bleaching under heat stress than did the warm-pool corals. But how do we know that these differences are greater than would be expected if the variation within and between samples represents nothing more than random variation? Here we will use some simple tests to see if the differences measured are significant (unlikely due to random variation).

Average chlorophyll ratio	Cool-pool corals	Warm-pool corals
0.0	0	0
0.1	0	0
0.2	1	0
0.3	1	0
0.4	4	0
0.5	7	0
0.6	1	0
0.7	1	1
0.8	2	3
0.9	0	3
1.0	0	1

QUESTIONS

Question 1

Prepare a bar graph based on these data. Display the chlorophyll ratios on the x axis, and show the number of corals that exhibited each ratio on the y axis.

Question 2

First, let’s consider if there is a significant effect of heat stress in each of the two groups. At the outset we assume that there is no effect of heat stress in either group—this is called our null hypothesis (H₀). We use statistical tests to decide if we can reject the null hypothesis and conclude that there is an effect of heat stress. If the null hypothesis is true, then we would expect that any differences in chlorophyll levels between control and experimental populations are due to random variation, and so we would expect the chlorophyll ratios to be greater than 1.0 as often as they are less than 1.0. In other words, the expected distribution of values < 1 and > 1 is like the expected distribution of heads and tails in a coin toss. Let’s first consider the cool-pool corals. There are 17 samples, and all 17 had chlorophyll ratios < 1.0. The probability of this happening at random is the same as getting 17 heads in 17 flips of a fair coin (by a “fair coin” we mean the probability of heads in one flip = 0.5). Using this criterion, calculate the probability of the null hypothesis (H₀: no effect of heat stress on bleaching) for each of the two populations.

For the cool-pool corals, the probability of H0 = (0.5)17 = 0.00000762939. Therefore we can safely reject H0 and conclude that there is indeed a significant effect of heat stress on coral bleaching (at P < 0.00001). In other words, if the null hypothesis were true and there were no real effect of heat stress on coral bleaching, we would expect to see this many chlorophyll ratios below 1.0 fewer than 1 time out of 100,000 trials. For the warm-pool corals, there are seven observed values < 1, and none > 1. In this case, the probability of H0 = (0.5)7 = 0.0078125. Therefore we can again reject H0 and conclude that there is a significant effect of heat stress on coral bleaching in warm-pool corals as well (this time at P < 0.01).

Question 3

Now let’s consider if there is a significant difference in the level of bleaching in the cool-pool versus the warm-pool corals. Our null hypothesis in this case is that the levels of bleaching are the same in both groups. If the null hypothesis is true, then we would expect (on average) the same distribution of chlorophyll ratios in the samples of both groups. From the Results section in the experiment, we see that the average chlorophyll ratio observed in the cool-pool samples is 0.5, and the average chlorophyll ratio observed in the warm-pool samples is 0.85. Would we expect a difference this great if the distributions of the two samples were drawn from the same underlying distribution of values? To find out, write each of the 25 observed chlorophyll ratios (from both groups) on an index card. Thoroughly mix and shuffle the cards to randomize their order, and then deal them into two groups of the same size as the cool-pool samples (17) and warm-pool samples (8). Calculate the average ratios in these randomized samples. Repeat this procedure or combine the results of your randomization test with those of other students in your class. How often do you see a difference as great as the observed difference in the two samples (0.85–0.5, or a difference of 0.35)?

The results of the randomization trials will differ depending on how well the cards are shuffled and how many replicates are compared, but the probability of finding a difference as great as 0.35 (the observed difference) in truly randomized samples of the two groups is very low (P < 0.001). Therefore we can again reject the null hypothesis and conclude that the effects of heat stress on coral bleaching are indeed higher in the corals from cool pools than in those from warm pools.

Question 4

What do these results suggest about the possible response of coral populations in different environments to ocean warming?

The different distributions of chlorophyll ratios for the cool- and warm-pool corals indicate that although both populations suffer bleaching as a consequence of heat stress, the populations from the cool pools are more sensitive. This suggests that corals from warmer environments might replace those from cooler environments under long-term conditions of global warming.

A similar work with the data exercise may be assigned in LaunchPad.

More specifically, statistical methods tell us the probability of obtaining the same results by chance even if the null hypothesis were true. We need to eliminate, insofar as possible, the chance that any differences showing up in the data are merely the result of random variation in the samples tested. Scientists generally conclude that the differences they measure are significant if statistical tests show that the probability of error (that is, the probability that a difference as large as the one observed could be obtained by mere chance) is 5 percent or lower. They often use more stringent criteria for rejecting the null hypothesis, however, depending on the consequences of accepting a wrong hypothesis. Appendix B of this book offers a short primer on statistical methods to which you can refer as you analyze data that will be presented throughout the text.