One key to Mendel’s success was his use of large numbers of plants. By counting many offspring from each cross, he observed clear patterns that allowed him to formulate his theories. After his work became widely recognized, geneticists began using simple probability calculations to predict the ratios of genotypes and phenotypes in the progeny of a given cross or mating. They use statistics to determine whether the actual results match the prediction (as explored in the work with the data exercise on p. 243).

248

You can think of probabilities by considering a coin toss. The basic conventions of probability are simple:

There are two possible outcomes of a coin toss, and both are equally likely, so the probability of heads is ½—as is the probability of tails.

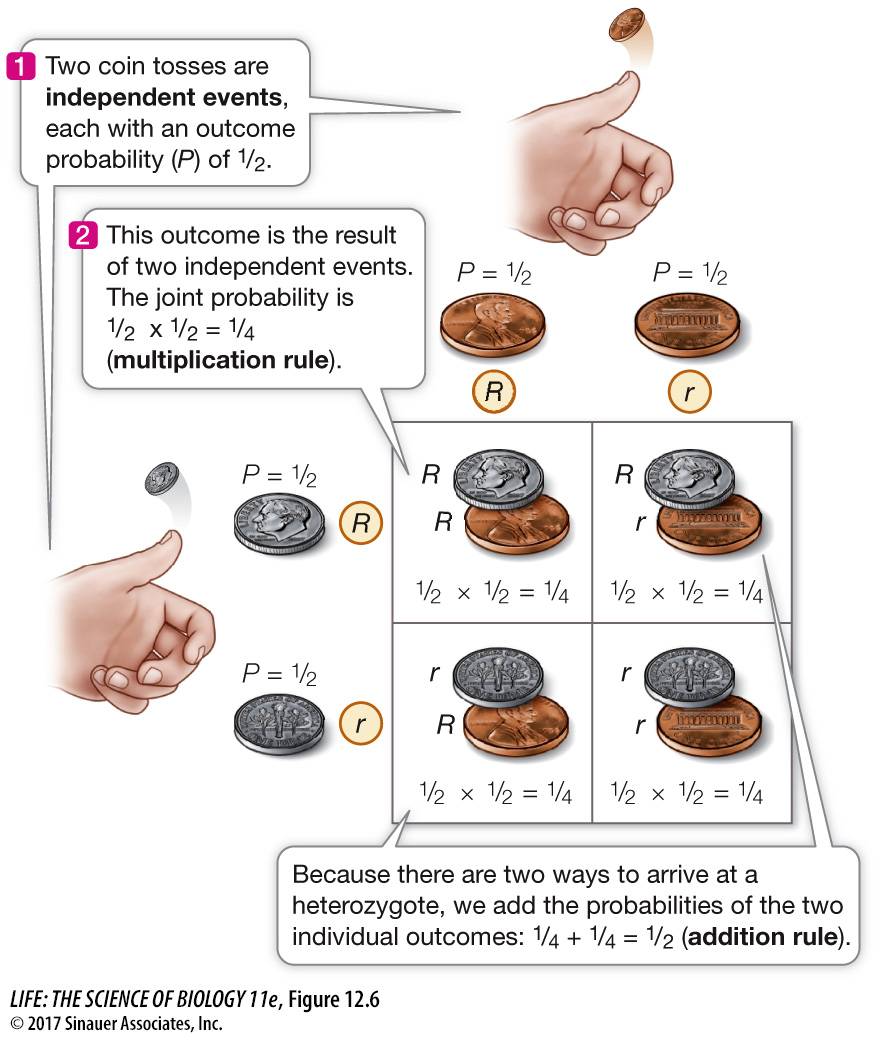
If two coins (say a penny and a dime) are tossed, each acts independently of the other (Figure 12.6). What is the probability of both coins coming up heads? In half of the tosses, the penny comes up heads, and in half of that fraction, the dime comes up heads. The probability of both coins coming up heads is ½ × ½ = ¼. In general, the probability of two independent outcomes occurring together is found by multiplying the two individual probabilities (the multiplication rule). The multiplication rule can be seen in the results of a monohybrid cross (see Figure 12.1). After the self-pollination of an Rr F₁ plant, the probability that an F₂ plant will have the genotype RR is ½ × ½ = ¼, because the chance that the sperm will have the genotype R is ½, and the chance that the egg will have the genotype R is also ½. Similarly, the probability of obtaining an rr offspring is also ¼.

Probability can also be used to predict the proportions of phenotypes in a dihybrid cross. Let’s see how this works for the experiment shown in Figure 12.4. Using the principles we just described, you can calculate the probability of an F₂ seed being round. This is found by adding the probability of obtaining an Rr heterozygote (½) to the probability of an RR homozygote (¼): a total of ¾ (the addition rule). By the same reasoning, the probability that a seed will be yellow is also ¾. The two characters are determined by separate genes and are independent of each other, so:

Looking at all four phenotypes, you can see that they are expected to occur in the ratio of 9:3:3:1.

A Punnett square or these simple probability calculations can be used to determine the expected proportions of offspring with particular phenotypes. In the dihybrid cross discussed above, about one-sixteenth of the F₂ seeds are expected to be wrinkled and green. But this does not mean that among 16 F₂ seeds there will always be exactly 1 wrinkled, green seed. For any toss of a coin, the probability of heads is independent of what happened in all the previous tosses. Even if you get three heads in a row, the chance of a head in the next toss is still ½, and it is quite possible to toss a coin four times and get four heads. But if you toss the coin many times, you are highly likely to get heads in about half of the tosses. If Mendel had examined only a few progeny in each of his crosses, it is unlikely that he would have observed the phenotypic ratios that he did observe. It was his large sample sizes that allowed him to identify the underlying patterns of inheritance.