Heterozygote advantage maintains polymorphic loci

In many cases, different alleles of a particular gene are advantageous under different environmental conditions. Most organisms experience a wide variety of environmental conditions over time. A night is dramatically different from the preceding day. A cold, cloudy day differs from a clear, hot one. Day length and temperature change seasonally. For many genes, a single allele is unlikely to perform well under all these conditions. In such cases, heterozygous individuals (with two different alleles) are likely to outperform individuals that are homozygous (with only one of those two alleles).

Colias butterflies of the Rocky Mountains live in environments where dawn temperatures are often too cold, and afternoon temperatures too hot, for the butterflies to fly. Populations of these butterflies are polymorphic for a gene that encodes the enzyme phosphoglucose isomerase (PGI), which influences how well a butterfly flies at different temperatures. Butterflies with certain PGI genotypes can fly better during the cold hours of early morning; others perform better during midday heat (Figure 20.17). The optimal body temperature for flight is 35°C–39°C, but some butterflies can fly with body temperatures as low as 29°C or as high as 40°C. During spells of unusually hot weather, heat-tolerant genotypes are favored; during spells of unusually cool weather, cold-tolerant genotypes are favored.

441

experiment

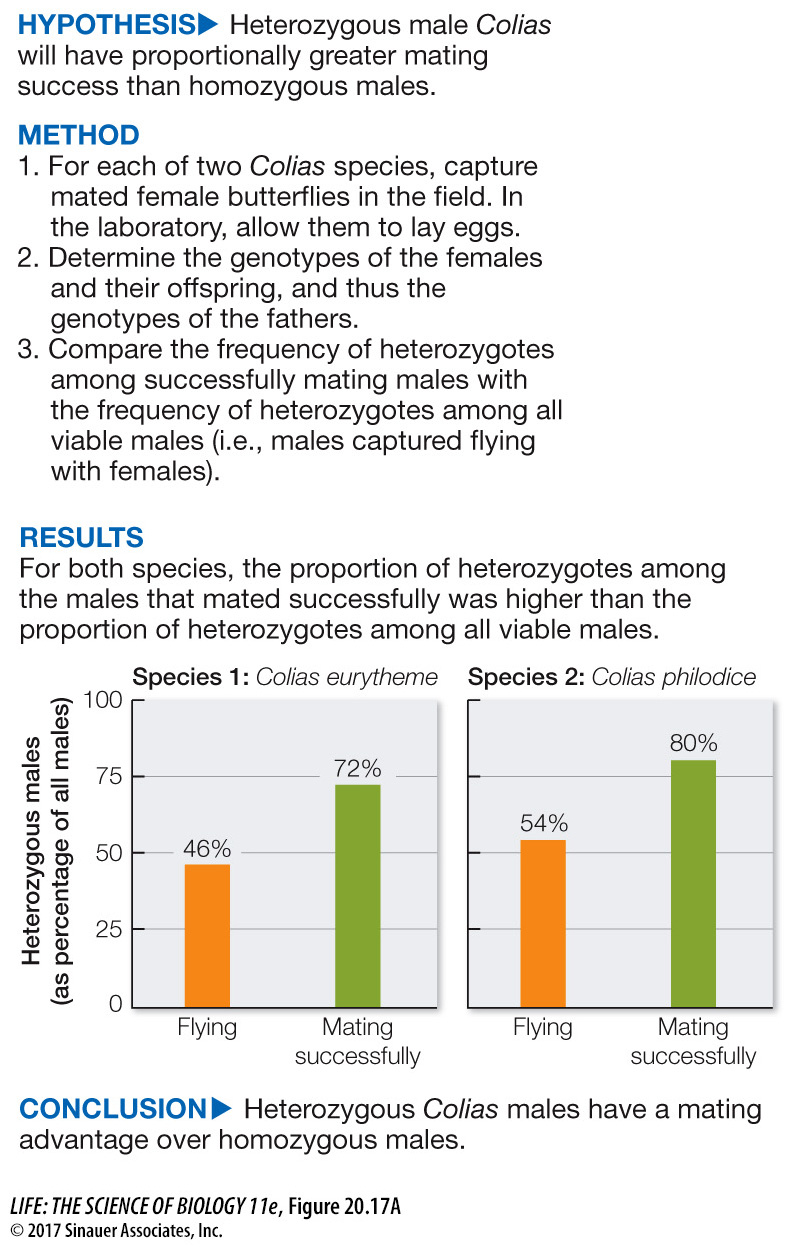
image

Figure 20.17A A Heterozygote Mating Advantage

Original Paper: Watt, W. B., P. A. Carter and S. M. Blower. 1985. Adaptation at specific loci. IV. Differential mating success among glycolytic allozyme genotypes of Colias butterflies. Genetics 109: 157–175.

Among butterflies of the genus Colias, males that are heterozygous for two alleles of the PGI enzyme can fly farther under a broader range of temperatures than males that are homozygous for either allele. Does this ability give heterozygous males a mating advantage?

work with the data

Figure 20.17B Do Heterozygous Males Have a Mating Advantage?

Original Paper: Watt, W. B., P. A. Carter and S. M. Blower. 1985.

Ward Watt and his colleagues tested the hypothesis that males with two different alleles for the PGI enzyme (heterozygotes) were more likely to mate successfully with females than were homozygous males. They reasoned that the heterozygous males could fly farther under a broader range of temperatures than could homozygous males, and that this ability would give heterozygous males greater access to receptive females. To test this hypothesis, they needed to know the frequency of heterozygotes among successfully mating males, and they needed to compare that frequency with the frequency of heterozygotes among males in the general population (i.e., all the potential mates available to females). To estimate the frequency of heterozygotes among mating males, Watt and his colleagues collected mated female butterflies in the field and allowed them to lay eggs in the laboratory. They hatched the eggs and determined the genotypes of the offspring, as well as the genotypes of the females. Using this information, they could determine the genotypes of the males that fathered the larvae. They then compared the estimated frequency of heterozygotes among the successful fathers with the frequency of heterozygotes among all viable males in the population. Samples of their data are given in the table.

All viable malesa Mating males
Species Heterozygous/
total		 Percent
heterozygous		 Heterozygous/
total		 Percent
heterozygous
C. philodice 32/74 43.2 31/50 62
C. eurytheme 44/92 47.8 45/59 76.3

a “Viable males” are males captured flying with females (hence the potential to mate).

QUESTIONS

Question 1

If we assume that the proportions of each genotype among mating males should be the same as the proportions seen among all viable males, what is the number of mating males expected to be heterozygous and homozygous in each sample?

For C. philodice, 43.2% of all viable males are heterozygous, so 56.8% must be homozygous. To get expected numbers of heterozygous and homozygous mating males, we multiple the expected proportions (from all viable males) by the total number of mating males sampled. Therefore we expect to see (0.432)(50) = 21.6 heterozygous mating males, and (0.568)(50) = 28.4 homozygous mating males. If we repeat the same calculations for C. eurytheme, we expect (under the given assumption) to see (0.478)(59) = 28.2 heterozygous mating males and (0.522)(59) = 30.8 homozygous mating males.

Question 2

Use a chi-square test (see Appendix B) to evaluate the significance of the difference in the observed and expected numbers of heterozygous and homozygous individuals among the mating males. The critical value (P = 0.05) of the chi-square distribution with one degree of freedom is 3.841. Are the observed numbers of genotypes among mating males significantly different (P < 0.05) from the expected numbers in these samples?

Chi-square calculations for C. philodice:

Genotype Expected (E) Observed (O) O – E (O – E)2 (O – E)2/E
Heterozygotes 21.6 31 9.4 88.36 4.091
Homozygotes 28.4 19 –9.4 88.36 3.111

The sum of the last column gives the chi-square test statistic: 7.202. Since this value is greater than the critical value (P = 0.05) of 3.841, the observed results are significantly different from the expectations at P < 0.05. In other words, we can reject the null hypothesis and conclude that the proportions of each genotype (heterozygotes and homozygotes) of mating males are significantly different from the proportions of these genotypes seen among all viable males in C. philodice.

Chi-square calculations for C. eurytheme:

Genotype Expected (E) Observed (O) O – E (O – E)2 (O – E)2/E
Heterozygotes 28.2 45 16.8 282.17 10.005
Homozygotes 30.8 14 –16.8 282.17 9.162

The sum of the last column gives the chi-square test statistic: 19.167. Since this value is greater than the critical value (P = 0.05) of 3.841, the observed results are significantly different from the expectations at P < 0.05. In other words, we can reject the null hypothesis and conclude that the proportions of each genotype (heterozygotes and homozygotes) of mating males are significantly different from the proportions of these genotypes seen among all viable males in C. eurytheme.

Question 3

The investigators determined the genotypes of enough larvae from each batch of eggs to judge the genotype of the father with 99% certainty. How many larvae did they need to measure to achieve that level of certainty?

Hint: If the female is homozygous—say, genotype ii—the number needed is small. However, if a female is heterozygous—say, genotype ij—and only ii and ij progeny are found among her offspring, more larvae need to be genotyped. In this particular case, the father can be only ii or ij. If he were ij, the probability that any one offspring is not jj = 0.75, so the chance of getting only ii and ij among n offspring is 0.75n. What value of n is required to reduce the probability of error in determining the father’s genotype to 0.01?

(0.75)16 is approximately 0.01002. Therefore the investigators would need to analyze at least 16 larvae from each batch of eggs to judge the genotype of the father with 99 percent certainty. An easy way to find this answer is to multiply 0.75 × 0.75, and then multiply the answer by 0.75, and continue until the result is approximately 0.01. Keep track of the number of times you multiply by 0.75 to find the appropriate sample size.

A similar work with the data exercise may be assigned in LaunchPad.

442

Heterozygous Colias butterflies can fly over a greater range of temperatures than homozygous individuals, which should give them an advantage in foraging and finding mates. A test of this prediction found that heterozygous males did indeed have a mating advantage, and further, that this advantage maintains the polymorphism in the population. Of course, the heterozygous genotype can never become fixed in the population, because the offspring of two heterozygotes will always include both classes of homozygotes in addition to heterozygotes.