Ion transporters and channels generate membrane potentials
943
The cell membranes of neurons, like those of all other cells, are lipid bilayers that are impermeable to ions but contain many protein molecules that serve as *ion transporters and ion channels. Ion transporters and channels are responsible for the distribution of charges across the membrane that determine membrane potential.
*connect the concepts The passive and active mechanisms that transport materials across cell membranes are discussed in Key Concepts 6.3 and 6.4. The passive mechanisms are membrane proteins that form channels (see Figure 6.10), and the active mechanisms (which require ATP) are membrane proteins engaged in active transport (see Figure 6.14).
Ion transporters require energy to move ions against their concentration or electrical gradients and are therefore called ion pumps. A major ion transporter in the cell membranes of neurons (and all other cells) is the sodium–
Ion channels permit the diffusion of ions across membranes. These channels are water-
Potassium channels are the most common open, or leak, channels in the cell membranes of resting (nonstimulated) neurons. As a consequence, resting neurons are more permeable to K+ than to any other ion. Thus, open potassium channels are largely responsible for the resting membrane potential. Because the potassium channels make the cell membrane permeable to K+, and because the Na+–K+ pump keeps the concentration of K+ inside the cell much higher than that outside the cell, K+ tends to diffuse down its electrochemical gradient, out of the cell, through the channels. But, if K+ ions left the cell they would leave behind unbalanced negative charges, generating an electric potential across the membrane that tends to pull K+ back into the cell.
The membrane potential at which the net diffusion of K+ out of the cell ceases (that is, the point at which K+ diffusion out due to the concentration gradient is balanced by its inward movement due to the negative electric potential) is the potassium equilibrium potential, or EK. The value of EK can be calculated from the concentrations of K+ on the two sides of the membrane using the Nernst equation (Figure 44.5A). This equation, developed in the late 1800s, shows that the existence of ion channels in neuronal membranes was hypothesized long before their specific structures and properties were discovered.
research tools
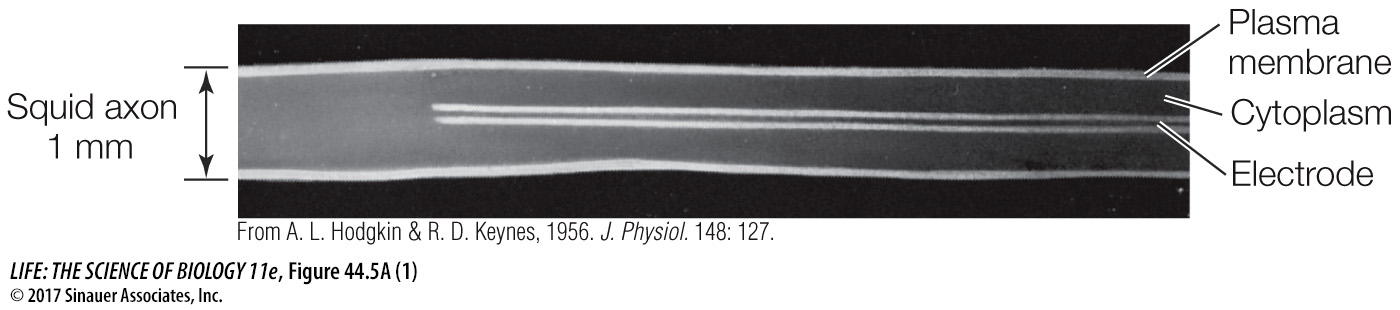
Figure 44.5A Using the Nernst Equation The Nernst equation calculates membrane potential when only one type of ion can cross a membrane that separates solutions with different concentrations of that ion.
Measure concentrations of ions inside and outside a neuron.
To measure the concentration of ions in a neuron, the neuron (and its axon) must be big. Squid have giant neurons that control their escape response (see Figure 44.13C). It is possible to sample the cytoplasm of these axons, which are about 1 mm in diameter.
Use the Nernst equation to calculate what the membrane potential would be if it were permeable to each of the ions that are differently concentrated on the two sides of the membrane: Na+, K+, Ca2+, and Cl–.
The Nernst equation predicts the membrane potential resulting from membrane permeability to a single type of ion that differs in concentration on the two sides of the membrane. The equation is written
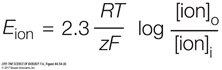
where E is the equilibrium (resting) membrane potential (the voltage across the membrane in mV), R is the universal gas constant, T is the absolute temperature, z is the charge on the ion, and F is the Faraday constant. The subscripts o and i indicate the ion concentrations outside and inside the cell, respectively.
At this point you could just “plug and play,” but do you understand this equation?
A concentration difference of ions across a membrane creates a chemical force that pushes the ions across the membrane by diffusion; however, the resulting unbalanced electric charges will pull the ions back the other way. At equilibrium, the two forces are in balance and there is no net movement of ions across the membrane.
The chemical energy pushing the ions will equal 2.3 RT log [ion]o/[ion]i
The electric energy pulling the ions will equal zEF. So, at equilibrium:
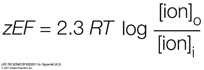
Rearranging the equation to solve for E, we get the Nernst equation:
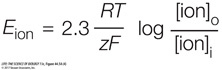
We can simplify the equation by picking a temperature—
let’s use “room temperature,” or 20ºC— and solving for 2.3 RT/F. At 20ºC, 2.3 RT/F equals 58. Thus: 
Measuring ion concentrations in squid giant axon cytoplasm and in seawater, then solving the Nernst equation for each ion, we find:
Ion concentration (mM) Predicted membrane
potential (mV)Ion in squid axon in seawater K+ 400 20 –75 Na+ 50 460 +56 Ca2+ 0.5 10 +38 Cl– 50 560 –60 Since the measured membrane potential is –66 mV, it is clear that the resting potential of the axon is due to permeability of the membrane to more than just one type of ion.
work with the data
Figure 44.5B Equilibrium Membrane Potential: The Goldman Equation
Original Papers: Goldman, D. E. 1943. Potential, impedence and rectification in membranes. Journal of General Physiology 27: 37–
Hodgkin, A. L. and B. Katz. 1949. The effect of sodium ions on the electrical activity of the giant axon of the squid. Journal of Physiology 108: 37–
Figure 44.5A presented the Nernst equation, by which the membrane potential for a single ion can be determined. But you also saw (at the end of Figure 44.5A) that the equilibrium membrane potential is the product of more than one ion. The Goldman equation (frequently called the Goldman, Hodgkin, Katz equation) calculates the equilibrium membrane potential by taking into account all of the ions that can diffuse across a given membrane and the relative permeabilities of the membrane to those ions. The ions involved in mammalian neurons here are K+, Na+, and Cl–, and the Goldman equation is

Relative permeabilities (p) are expressed as ratios. The membrane’s permeability to potassium ions is the highest, so pK =1.0. Then pNa = 0.05 and pCl = 0.44. Bracketed elements refer to the inside and outside ion concentrations, as in the Nernst equation.
QUESTIONS
Question 1
The table gives the intra-
| Ion concentration (mM) | ||
|---|---|---|
| Intracellular | Extracellular | |
| K+ | 140 | 5 |
| Na+ | 10 | 145 |
| Cl– | 20 | 110 |
Plugging the values in the table into the equation gives:
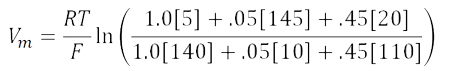
Substituting 2.3RT/F log for RT/F ln:
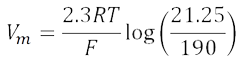
Assuming T = room temperature, 2.3RT/F = 58 (see Figure 44.5).
So,
Vm = 58 log 0.1118
Vm = –55.2 mV
If you use the Nernst equation:
K+: EK = 58 log (5/140) = –84 mV
Na+: ENa = 58 log (145/10) = +67 mV
Cl–: ECl = 58 log (110/20) = +43 mV
Clearly the membrane potential is not due to K+ alone. The membrane permeabilities to Na+ and to Cl– have a slight depolarizing influence on the resting potential of the mammalian neuron.
A similar work with the data exercise may be assigned in LaunchPad.
In the late 1940s, A. L. Hodgkin and A. F. Huxley at the University of Cambridge set out to study the electrical properties of axonal membranes. With the techniques available at that time, the necessary measurements could be made only if you had a very large axon to work with. Such an axon exists in nature—
The resting potential of a neuron is less negative than the EK calculated from the Nernst equation. This means that the resting potential is not due solely to leak K+ channels. The neuronal membrane is slightly permeable to other ions, especially Na+ and Cl–, and movements of these ions influence the resting potential. A different equation takes into account (1) all of the ions that can cross the membrane and (2) the relative permeability of the membrane to those ions. This equation, called the Goldman equation, predicts the membrane potential more accurately than does the Nernst equation (Figure 44.5B).