Accuracy, Precision, and Significant Digits
There are two kinds of numbers in the world—exact and inexact. For instance, counting is exact because you can safely say that there are exactly 12 eggs in a dozen. However, no measurement with a ruler, a balance, or a graduated cylinder is ever exact. So, when a measurement or the average of several measurements comes out extremely close to the actual true value, we say that the measurement or average is accurate.
If you measure something several times and get very similar answers each time, your measurements are precise.
The ability to make precise measurements depends partly on the equipment used. For example, a graduated cylinder is more precise than a beaker. Precision also depends on how carefully a measurement was made. For example, a measurement of 23.76 mL is more precise than a measurement of 24 mL.
To understand the difference between precision and accuracy, imagine a lab experiment to measure the boiling point of water at sea level. Several readings are taken: 97.2 °C, 97.0 °C, and 97.1 °C. The measurements are close to each other; repeating the experiment would likely give similar results, so they are precise. However, they are not accurate; the boiling point of water at sea level is known to be 100 °C. Perhaps the thermometer was faulty, or the person taking the measurements consistently read the thermometer incorrectly.
Using significant digits in a measurement allows you to indicate the degree of certainty in the measurements. In general, the last digit of any measurement is uncertain. For example, suppose you use a meterstick, marked in millimeters, to measure the length of an object. If you record a measurement of 24.33 cm, the last digit is an estimate based on the closest millimeter markings and is not certain. Another person might measure the length as 24.34 cm or 24.32 cm. However, you will both agree on the 24.3 because you can read the meterstick accurately to the millimeter, or 0.1 cm. The measurement 24.33 has four significant digits.
A-2
The rules for determining the number of significant digits are complicated. Nonzero digits always count. Zeros sometimes count depending on where they are. Zeros might be leading, trapped, or trailing.
Leading zeros, such as those in 0.004728, never count as significant digits.
Trapped zeros, as in 1.08, always count as significant digits.
Trailing zeros, or those at the end of a number, count only when there is a decimal point. In the numbers 20.0, 300.00, and even 50., the zeros count as significant digits. If there is no decimal point, as in 500, then it isn’t possible to tell whether the zeros are significant. Sometimes you can deduce that zeros are significant based on the instrumentation. For example, a thermometer generally measures to the nearest degree. You can use scientific notation to avoid ambiguity. The measurement 5.00 × 102 has three significant digits, whereas the measurement 5× 102 has only one significant digit.
As you do calculations involving numbers with different numbers of significant digits, follow these two rules.
Adding or subtracting: Your final answer will have only as many decimal places as the measurement with the fewest decimal places.
Multiplying or dividing: The result can have only as many significant digits as the number with the fewest significant digits.
As you add, multiply, or combine measurements in other ways, you will often have to round the result of your calculation to obtain the correct number of significant digits.
Example 1
Rounding the Sum or Difference
Calculate each sum or difference and round the answer to the appropriate number of significant digits.
2.24 + 3.4 + 5.231
10.5 cm – 3.36 cm
Solution
First add the numbers to get the sum 10.871. Then consider the decimal places to arrive at the final answer.
2 decimal places 2.24 1 decimal place 3.4 3 decimal places + 5.231 10.871 Because 3.4 has only one decimal place, the sum should be rounded to 10.9. Always complete the calculation before rounding.
First subtract the numbers.
1 decimal place 10.5cm 2 decimal places – 3.36 cm 7.14 cm Because 10.5 has only one decimal place, round the final answer to one decimal place: 7.1 cm.
A-3
Example 2
Rounding a Product
Calculate each product and round to the appropriate number of significant digits.
12.34 · 1.6
4.71 m · 5.28 m
Solution
First multiply the two decimals.
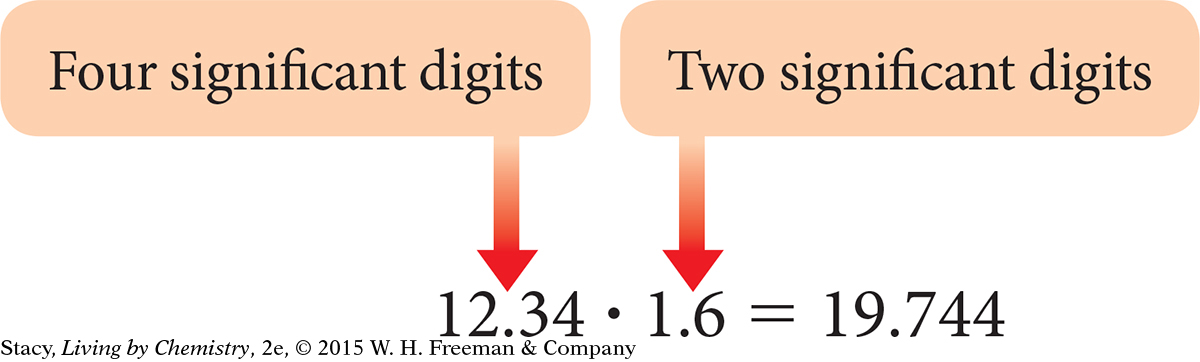
Because there are only two significant digits in 1.6, you can have only two significant digits in your answer. You must round the product to 20. You might write this answer as to make it clear that both digits are significant.
First multiply: 4.71 m · 5.28 m 524.8688 m2.
Both factors have three significant digits, so the answer must be rounded to three significant digits: 24.9 m2.
Practice Exercises
How many significant digits are in each of these numbers?
20.1
300.0
0.0031
0.03010
Complete these calculations.
2 5.14 + 3.4 + 1 5.031
100.04 cm – 7.362 cm
3005 · 4 5.20
What is the volume of a box 14.5 cm by 1 5.9 cm by 21.1 cm?
The density of copper is 8.92 g/cm3. What is the mass of 24 cm3 of copper?
Answers
1a. 3
1b. 4
1c. 2
1d. 4
2a. 43.5
2b. 92.68
2c. 135,800
4830 cm3
210 g