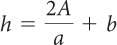Solving Equations

Solving chemistry problems sometimes involves solving a math equation. When the quantity you are looking for is isolated, or alone on one side of the equation, all you need to do is complete the calculations. A simple example is finding the Fahrenheit equivalent of 28 °C using the equation

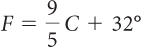
image

Sometimes the quantity that answers your question is not alone on one side of the equation. To solve these problems, isolate the variable you are looking for on one side of the equation, so that calculations that will lead to your answer are on the other side of the equation. For example, to find a temperature in degrees Celsius, rearrange the equation in terms of C.

A-4

Start with the known relationship image
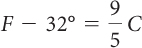
Subtract 32° from both sides image
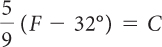
Multiply both sides byimage image

Now that C is isolated, you can substitute any Fahrenheit temperature and carry out the calculations to find the corresponding Celsius temperature.

Example 1

Solving for x

Solve these equations for x.

  1. 0.1x + 12 = 2.2

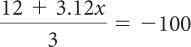
  2. image

Solution

a. Original equation.

0.1x + 12 = 2.2
Subtract 12 from both sides.

0.1x + 12 – 12 = 2.2 – 12

0.1x = –9.8
Divide both sides by 0.1.

x = –98
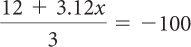
b. Original equation. image
Multiply both sides by 3.

12 + 3.12x = –300
Subtract 12 from both sides.

–12 + 12 + 3.12x = –300 – 12

3.12x = –312
Divide both sides by 3.12.

x = –100

Example 2

Solving for V2

Solve this equation for V2.

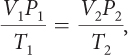
image

for V2

Solution

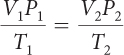
Original equation. image
Multiply both sides by T2;
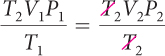
remove the factor of 1.		 image
Divide both sides by P2;
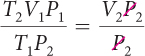
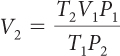
remove the factor of 1.		 image
image

The equation is now expressed in terms of V2. Substituting in values for the other five variables will give a value for V2.

A-5

Practice Exercises

  1. Solve these equations. Indicate the action you take at each stage.

    1. 144x + 33 = 45

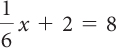
    2. image

    3. 5(x − 7) = 15+ 52

  2. Solve these equations for the variable indicated.

    1. d = rt, for t

    2. P = 2(l + w), for w

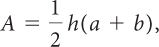    3. image for h

Show Answers

Answers

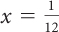  1. 1a. image (On both sides, subtract 33 and divide by 144.)

  2. 1b. x = 36 (On both sides, subtract 2 then multiply by 6.)

  3. 1c. x = 15 (Combine 15 and 25 on the right side, divide both sides by 5, and add 7 to both.)

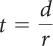
  4. 2a. image

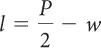
  5. 2b. image

  6. 2c. image