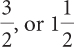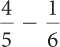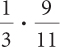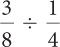Ratios and Proportions
As chemists study matter, they are often working with ratios. The four statements here all express some sort of ratio.
Density is the ratio of mass to volume: D = m/V.
The units of molar mass are g/mol.
The mole ratio of H2 to O2 is 2:1.
The reaction gave a 78% yield.
Ratios can be written as fractions. For instance, 78% is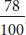 
. The ratio 2:1 can be written 
. Ratios can be reduced like fractions, or they can be added once they have a common denominator. Unit fractions, which equal 1 because the numerator is equivalent to the denominator, can be used to convert between units or to create equivalent fractions.
Whenever you are working with ratios, use the rules for working with fractions.
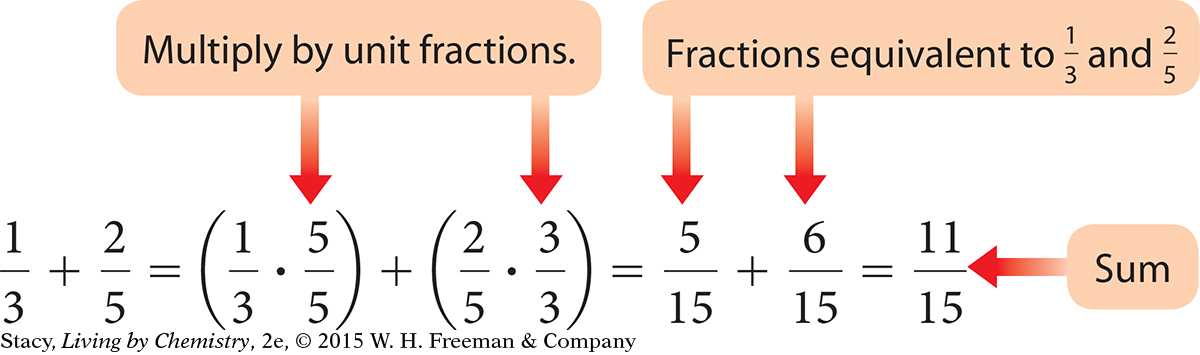
To create equivalent fractions, multiply a fraction by a unit fraction. In a unit fraction, the numerator is equivalent to the denominator. A unit fraction is equal to 1 and can be used to convert between units or create equivalent fractions.
To add or subtract fractions, find equivalent fractions with a common denominator, then add or subtract the numerators and put that number over the common denominator.
A-12
To multiply fractions, multiply the two numerators, and multiply the two denominators. You may want to reduce the fraction so that there are no common factors between the numerator and the denominator.
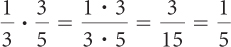
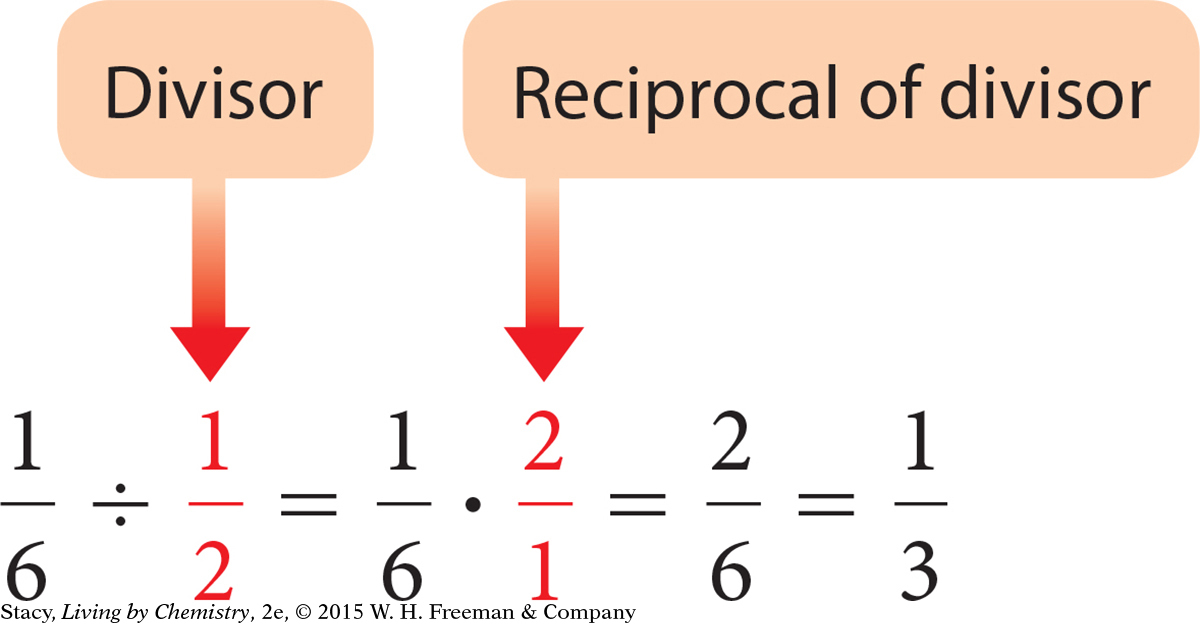
To divide fractions, multiply by the reciprocal of the divisor.
To reduce a fraction, divide the numerator and denominator by any factor they have in common; this is often referred to as canceling.
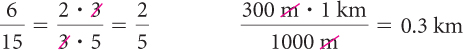
Proportions are equations that state two ratios are equal. Each of the equations shown here is a proportion.
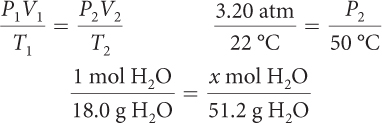
Proportions can be solved by multiplying (or dividing) both sides of the equation by the same value. As you solve chemistry problems, you will often use ratios and proportions.
Example 1
Limiting Reactant
Imagine you start with 10.0 g of Mg(OH)2 and 100.0 mL of 4.0 M HCl. How much MgCl2 will be produced?
Solution
Write the balanced chemical equation.
Mg(OH)2(s) + 2HCl(aq) → MgCl2(aq) + 2H2O(l)
Determine the molar masses of each compound.
| Reactants: Mg(OH)2 = 58.3 g/mol | HCl = 36.5 g/mol |
| Products: MgCl2 = 9 5.2 g/mol | H2O = 18.0 g/mol |
Determine the number of moles of each reactant that you have.
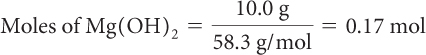
Moles of HCl = (0.100 L)(4.0 mol/L) = 0.40 mol
Use the mole ratio to identify the limiting reactant.
A-13
The reactants combine in a 1:2 ratio. So you need 0.17 mol · 2 = 0.34 mol of hydrochloric acid, HCl, to react with the 0.17 mol of magnesium hydroxide, Mg(OH)2.
You have 0.40 mol of HCl, which is plenty, so the limiting reactant is Mg(OH)2. When the reaction is complete, there will be 0.06 mol of HCl left over.
Use the limiting reactant to determine the maximum amount of product.
For every 1 mol of Mg(OH)2, 1 mol of MgCl2 is produced.
So 0.17 mol of MgCl2 is produced. Use the molar mass of MgCl2 to determine the mass of MgCl2.
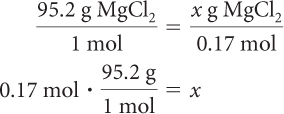
Example 2
Percent Yield
Suppose you ran the reaction from Example 1 again, this time starting with 3 5.0 g Mg(OH)2 and the same amount of HCl as before. In the laboratory, 1 5.4 g of MgCl2 are produced. What is the percent yield of your reaction?
Solution
First, determine the number of moles of each reactant you have. This will make it possible to identify the limiting reactant.
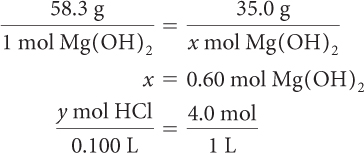
y = 0.40 mol HCl
The mole ratio of reactants is 1:2, so you need 1.2 mol of HCl to react with 0.60 mol of Mg(OH)2. You have only 0.40 mol of HCl available, so this time HCl is the limiting reagent.
It takes 2 mol of HCl to produce each mole of MgCl2, so you can expect to produce
0.20 mol of MgCl2: 
.
Next, use the molar mass of MgCl2 to calculate the theoretical yield.
x = 19 g
Now you can calculate the percent yield for the reaction you ran. Percent yield is yield per 100, or yield/100.
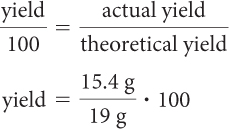
Percent yield 581%
Your percent yield was significantly lower than 100%.
Practice Exercises
A-14
What ratios and proportions appear in Examples 1 and 2?
Write each expression as a fraction.
68%
3:4
the ratio of volume to temperature
grams per cubic centimetre
Complete these calculations.
Answers
1. 
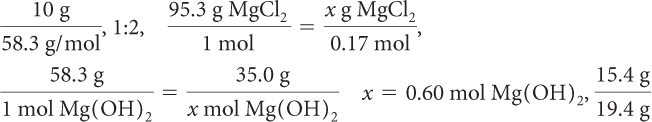
2a.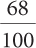 
2b. 
2c. volume/temperature, or 
2d.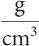 
3a.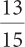 
3b.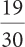 
3c. 
3d. 